(ENEM 2010 - 1ª Aplicação).
Um professor dividiu a lousa da sala de aula em quatro partes iguais. Em seguida, preencheu 75% dela com conceitos e explicações, conforme a figura seguinte.

Algum tempo depois, o professor apagou a lousa por completo e, adotando um procedimento semelhante ao anterior, voltou a preenchê-la, mas, dessa, vez, utilizando 40% do espaço dela. Uma representação possível para essa segunda situação é

Inicialmente, note que:
[tex] 40 \% = \frac{40}{100} = \frac{2}{5} [tex]
Assim, preencher 40% da lousa corresponde a dividi-la em 5 partes iguais e ocupar 2 partes com conceitos e explicações.
Desse modo, uma possível representação para essa situação é a Opção C:
(ENEM 2010 - 1ª Aplicação).
No monte de Cerro Armazones, no deserto de Atacama, no Chile, ficará o maior telescópio da superfície terrestre, o Telescópio Europeu Extremamente Grande (E-ELT). O E-ELT terá um espelho primário de 42 m de diâmetro, “o maior olho do mundo voltado para o céu”.
Disponível em htttp://www.estadao.com.br. Acesso em: 27 abr. 2010 (adaptado).
Ao ler esse texto em uma sala de aula, uma professora fez uma suposição de que o diâmetro do olho humano mede aproximadamente 2,1 cm.
Qual a razão entre o diâmetro aproximado do olho humano, suposto pela professora, e o diâmetro do espelho primário do telescópio citado?
A razão entre o diâmetro aproximado do olho humano e o diâmetro do espelho primário do telescópio citado é dado por
[tex] Razão = \frac{Diâmetro_{(olho)}}{Diâmetro_{(espelho)}} = \frac{2,1\ cm}{42\ m} [tex]
[tex] = \frac{2,1\ cm}{42\ 000\ cm} = \frac{1}{2\ 000} [tex]
Daí, a razão é:
[tex] \frac{1}{2\ 000}\ ou\ 1 : 2\ 000 [tex]
(ENEM 2010 - 1ª Aplicação).
Alguns testes de preferência por bebedouros de água foram realizados com bovinos, envolvendo três tipos de bebedouros, de formatos e tamanhos diferentes. Os bebedouros 1 e 2 têm a forma de um tronco de cone circular reto, de altura igual a 60 cm, e diâmetro da base superior igual a 120 cm e 60 cm, respectivamente. O bebedouro 3 é um semicilindro, com 30 cm de altura, 100 cm de comprimento e 60 cm de largura. Os três recipientes estão ilustrados na figura.

A escolha do bebedouro. In: Biotemas. V.22, no . 4, 2009 (adaptado).
Considerando que nenhum dos recipientes tenha tampa, qual das figuras a seguir representa uma planificação para o bebedouro 3?

O sólido que representa o bebedouro 3 é um semicilindro circular reto, cuja base é um semicírculo de diâmetro 60 cm e a superfície lateral é limitada por um retângulo de altura 100 cm; das figuras apresentadas, a que melhor representa a planificação é aquela que aparece na alternativa E.
(ENEM 2010 - 1ª Aplicação).
Uma fábrica produz barras de chocolates no formato de paralelepípedos e de cubos, com o mesmo volume. As arestas da barra de chocolate no formato de paralelepípedo medem 3 cm de largura, 18 cm de comprimento e 4 cm de espessura.
Analisando as características das figuras geométricas descritas, a medida das arestas dos chocolates que têm o formato de cubo é igual a
Sendo "a" a medida da aresta do cubo, em centímetros, do enunciado, temos:
[tex] Volume_{(cubo)} = Volume_{(paralelepípedo)} [tex]
[tex] a^{3} = c \cdot l \cdot h [tex]
[tex] a^{3} = 3 \cdot 18 \cdot 4 [tex]
[tex] a = \sqrt[3]{216} [tex]
[tex] a = 6 [tex]
(ENEM 2010 - 1ª Aplicação).
A classificação de um país no quadro de medalhas nos Jogos Olímpicos depende do número de medalhas de ouro que obteve na competição, tendo como critério de desempate o número de medalhas de prata seguido do número de medalhas de bronze conquistados. Nas Olimpíadas de 2004, o Brasil foi o décimo sexto colocado no quadro de medalhas, tendo obtido 5 medalhas de ouro, 2 de prata e 3 de bronze. Parte desse quadro de medalhas é reproduzida a seguir.

Disponível em: http://www.quadroademedalhas.com.br. Acesso em: 05 abr. 2010 (adaptado).
Se o Brasil tivesse obtido mais 4 medalhas de ouro, 4 de prata e 10 de bronze, sem alterações no número de medalhas dos demais países mostrados no quadro, qual teria sido a classificação brasileira no quadro de medalhas das Olimpíadas de 2004?
Se tivesse obtido mais 4 medalhas de ouro, 4 de prata e 10 de bronze, o Brasil teria terminado as Olimpíadas de 2004 com:
Ouro = 5 + 4 = 9 medalhas
Prata = 2 + 4 = 6 medalhas
Bronze = 3 + 10 = 13 medalhas
Assim, teria o mesmo número de medalhas de ouro que Cuba e a Ucrânia, perdendo para Cuba e ganhando da Ucrânia no número de medalhas de prata. Portanto ficaria na 12ª- colocação.
(ENEM 2010 - 1ª Aplicação).
Os dados do gráfico foram coletados por meio da Pesquisa Nacional por Amostra de Domicílios.

Fonte: IBGE. Disponível em: http://www.ibge.gov.br. Acesso em: 28 abr. 2010(adaptado).
Supondo-se que, no Sudeste, 14900 estudantes foram entrevistados nessa pesquisa, quantos deles possuíam telefone móvel celular?
Analisando o gráfico, é possível verificar que 56% dos estudantes entrevistados possuíam telefone móvel. Logo, 56% do total de entrevistados (14900) é igual a:
14 900 ------ 100 %
x ------ 56 %
[tex] x = \frac{14\ 900\ \cdot\ 56}{100} = 8\ 344 [tex]
Portanto, 8344 dos entrevistados da região sudeste possuíam telefone móvel celular.
(ENEM 2010 - 1ª Aplicação).
Acompanhando o crescimento do filho, um casal constatou que, de 0 a 10 anos, a variação da sua altura se dava de forma mais rápida do que dos 10 aos 17 anos e, a partir de 17 anos, essa variação passava a ser cada vez menor, até se tornar imperceptível. Para ilustrar essa situação, esse casal fez um gráfico relacionando as alturas do filho nas idades consideradas.
Que gráfico melhor representa a altura do filho desse casal em função da idade?

A altura dos filhos é sempre crescente e não dá saltos, é continua. De 0 a 10 anos esse crescimento da altura é mais intenso, logo uma reta com coeficiente angular maior (ângulo com a horizontal maior).
Dos 10 aos 17 o crescimento é menos intenso, logo uma reta com coeficiente angular menor (ângulo com a horizontal menor).
Dos 17 em diante o crescimento vai ficando cada vez menos intenso até se tornar imperceptível e, então, o coeficiente angular da reta se anula (ângulo com a horizontal é 0°.
Vê-se:

Percebe-se no gráfico A, que as alturas são representadas por retas, com ângulos em sequência decrescente e coeficientes angulares, também, decrescentes o que indica um crescimento que vai perdendo intensidade até se anular.
(ENEM 2010 - 1ª Aplicação).
Em sete de abril de 2004, um jornal publicou o ranking de desmatamento, conforme gráfico, da chamada Amazônia Legal, integrada por nove estados.

Disponível em: www.folhaonline.com.br. Acesso em: 30 abr. 2010 (adaptado).
Considerando-se que até 2009 o desmatamento cresceu 10,5% em relação aos dados de 2004, o desmatamento médio por estado em 2009 está entre
Analisando as informações do gráfico e calculando a média (M) do somatório dos índices de desmatamento por Km² no ano de 2004, encontra-se aproximadamente igual a:
[tex] M_{(2004)} = \frac{4+136+326+549+766+747+3463+3293+10416}{9} [tex]
[tex] M_{(2004)} = 2\ 638,9[tex]
Porém, com o aumento de 10,5% do desmatamento até o ano de 2009, essa média passou a ser:
[tex] M_{(2009)} =1,105 \cdot 2\ 638,9 = 2\ 916[tex]
que é um valor que se encontra entre 2800 e 3200.
(ENEM 2010 - 1ª Aplicação).
A resistência elétrica e as dimensões do condutor
A relação da resistência elétrica com as dimensões do condutor foi estudada por um grupo de cientistas por meio de vários experimentos de eletricidade. Eles verificaram que existe proporcionalidade entre:
• resistência (R) e comprimento (L), dada a mesma secção transversal (A);
• resistência (R) e área da secção transversal (A). dado o mesmo comprimento (L) e
• comprimento (L) e área da secção transversal (A), dada a mesma resistência (R).
Considerando os resistores como fios, pode-se exemplificar o estudo das grandezas que influem na resistência elétrica utilizando as figuras seguintes.

Disponível em: http://www.efeitojoule.com. Acesso em: abr. 2010 (adaptado)
As figuras mostram que as proporcionalidades existentes entre resistência (R) e comprimento (L), resistência (R) e área da secção transversal (A), e entre comprimento (L) e área da secção transversal (A) são, respectivamente,
Na 1ª figura dada, a mesma secção transversal (A), dobrando o comprimento a resistência também dobra, portanto é possível observar que a resistência (R) e o comprimento (L) são grandezas diretamente proporcionais.
Na 2ª figura, dado o mesmo comprimento, dobrando a área é observado que a resistência se reduziu à metade. Portanto, resistência e área são grandezas inversamente proporcionais.
Na 3ª figura dada, a mesma resistência (R), dobrando o comprimento (L) é observado que a área da secção transversal (A) também dobra, logo, o comprimento e a área da secção transversal são grandezas diretamente proporcionais. 1ª Figura: direta, 2ª Figura: inversa, 3ª Figura: direta.
[tex] R = ρ \cdot \frac{L}{A} [tex]
(ENEM 2010 - 1ª Aplicação).
Os dados do gráfico seguinte foram gerados a partir de dados colhidos no conjunto de seis regiões metropolitanas pelo Departamento Intersindical de Estatística e Estudos Socioeconômicos (Dieese).

Disponível em: http://g1.globo.com. Acesso em: 28 abr. 2010 (adaptado).
Supondo que o total de pessoas pesquisadas na região metropolitana de Porto Alegre equivale a 250 000, o número de desempregados em março de 2010, nessa região, foi de
Do gráfico, temos que 9,8% das 250.000 pessoas pesquisadas em Porto Alegre estão desempregadas. O número de desempregados entre os pesquisados em março de 2010 é dado por:
250 000 ------ 100%
x ----- 9,8 %
[tex] x = \frac{250\ 000\ \cdot\ 9,8}{100} = 24\ 500 [tex]
ou seja, 24.500 pessoas.
(ENEM 2010 - 1ª Aplicação).
A siderúrgica “Metal Nobre” produz diversos objetos maciços utilizando o ferro. Um tipo especial de peça feita nessa companhia tem o formato de um paralelepípedo retangular, de acordo com as dimensões indicadas na figura que segue.

O produto das três dimensões indicadas na peça resultaria na medida da grandeza
O produto das três dimensões é:
2,5 m × 0,5 m × 1,3 m = 1,625 m³
que representa a medida da grandeza volume.
(ENEM 2010 - 1ª Aplicação).
A figura I abaixo mostra um esquema das principais vias que interligam a cidade A com a cidade B. Cada número indicado na figura II representa a probabilidade de pegar um engarrafamento quando se passa na via indicada, Assim, há uma probabilidade de 30% de se pegar engarrafamento no deslocamento do ponto C ao o ponto B, passando pela estrada E4, e de 50%, quando se passa por E3. Essas probabilidades são independentes umas das outras.

Paula deseja se deslocar da cidade A para a cidade B usando exatamente duas das vias indicadas, percorrendo um trajeto com a menor probabilidade de engarrafamento possível.
O melhor trajeto para Paula é
Através das informações do enunciado temos:
Primeiro, vamos calcular a probabilidade de NÃO pegar engarrafamento no 1º e nem no 2º trecho:
Trajeto E1E3: (1 – 0,8)∙(1 – 0,5) = 0,1.
Trajeto E1E4: (1 – 08)∙(1 – 0,3) = 0,14.
Trajeto E2E5: (1 – 0,7)∙(1 – 0,4) = 0,18.
Trajeto E2E6: (1 – 0,7)∙(1 – 0,6) = 0,12.
Agora, iremos calcular a probabilidade de pegar engarrafamento pelo menos um trecho:
Trajeto E1E3: 1 – 0,1 = 0,90.
Trajeto E1E9: 1 – 0,14 = 0,86.
Trajeto E2E5: 1 – 0,18 = 0,82.
Trajeto E2E6: 1 – 0,12 = 0,88.
Assim, o melhor trajeto para Paula é o trajeto com a menor probabilidade de engarrafamento possível sendo o trajeto E2E5.
(ENEM 2010 - 1ª Aplicação).
O gráfico a seguir apresenta o gasto militar dos Estados Unidos, no período de 1988 a 2006.

Almanaque Abril 2008. Editora Abril.
Com base no gráfico, o gasto militar no início da guerra no Iraque foi de
Observando os dados fornecido pelo gráfico, o gasto militar dos EUA no início da guerra do Iraque foi de U$ 417,4 bilhões, que corresponde a U$ 417.400.000.000,00.
(ENEM 2010 - 1ª Aplicação).
Uma professora realizou uma atividade com seus alunos utilizando canudos de refrigerante para montar figuras, onde cada lado foi representado por um canudo. A quantidade de canudos (C) de cada figura depende da quantidade de quadrados (Q) que formam cada figura. A estrutura de formação das figuras está representada a seguir.

Que expressão fornece a quantidade de canudos em função da quantidade de quadrados de cada figura?
A progressão aritmética (4; 7; 10; 13; ...) representa a quantidade (C) de canudos de acordo com os seus termos, esta progressão possui razão (r) igual a 3 e primeiro termo 4, utilizando tais dados na fórmula do termo geral da P.A:
[tex] a_{n} = a_{1} + (n - 1)r [tex]
Assim, os termos dessa PA permitem estabelecer a lei de formação:
[tex] a_{n} = 4 + (n - 1) \cdot 3 = 4 + 3n -3 [tex]
[tex] a_{n} = 3n + 1 [tex]
(ENEM 2010 - 1ª Aplicação).
A loja Telas & Molduras cobra 20 reais por metro quadrado de tela, 15 reais por metro linear de moldura, mais uma taxa fixa de entrega de 10 reais.
Uma artista plástica precisa encomendar telas e molduras a essa loja, suficientes para 8 quadros retangulares (25 cm x 50 cm). Em seguida, fez uma segunda encomenda, mas agora para 8 quadros retangulares (50 cm x 100 cm). O valor da segunda encomenda será
área = 25 × 50 × 8 = 10 000 cm² = 1 m²
moldura = (50 × 2 + 25 × 2) × 8 = 1200 cm = 12 m
∴ custo = 20 × 1 + 15 × 12 + 10 = 210,00 reais
área = 50 × 100 × 8 = 40000 cm² = 4 m²
moldura = (50 v 2 + 100 × 2) × 8 = 2400 cm = 24 m
∴ custo = 20 × 4 + 15 v 24 + 10 = 450,00 reais
Portanto, o valor da segunda encomenda é maior do que o da primeira, mas não o dobro.
(ENEM 2010 - 1ª Aplicação).
Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.

Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá
[tex] Volume_{(leiteira)} = 20 \cdot Volume_{(xícara)} [tex]
[tex] π \cdot 4^{2} \cdot h = 20 \cdot π \cdot 2^{2} \cdot 2 [tex]
[tex] 16 \cdot π \cdot h = 160 \cdot π [tex]
[tex] h = \frac{160 \cdot π }{16 \cdot π} = 10\ cm [tex] (metade)
(ENEM 2010 - 1ª Aplicação).
Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r quilômetros de distância do centro da Terra. Quando r assume seus valores máximo e mínimo, diz-se que o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha que, para esse satélite, o valor de r em função de t seja dado por

Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.
O cientista deveria concluir que, periodicamente, S atinge o valor de
Sendo que:
[tex] r(t) = \frac{5\ 865}{1+ 0,15\ \cdot\ (0,06t)} [tex]
r assume seu apogeu com t = –1 e seu perigeu com t =1.
Logo,
[tex] r(t)_{(apogeu)} + r(t)_{(perigeu)} [tex]
[tex] = \frac{5\ 865}{1+ 0,15\ \cdot\ (-1)} + \frac{5\ 865}{1+ 0,15\ \cdot\ (+1)} [tex]
[tex] = 6\ 900 + 5\ 100 = 12 000 [tex]
(ENEM 2010 - 1ª Aplicação).
Uma empresa vende tanques de combustíveis de formato cilíndrico, em três tamanhos, com medidas indicadas nas figuras. O preço do tanque é diretamente proporcional à medida da área da superfície lateral do tanque. O dono de um posto de combustível deseja encomendar um tanque com menor custo por metro cúbico de capacidade de armazenamento.

Qual dos tanques deverá ser escolhido pelo dono do posto? (Considere π = 3).
Do enunciado, temos a tabela seguinte, que considera os cilindros circulares retos:
Área lateral: [tex] A_{L} = 2 \cdot 3 \cdot 2 \cdot 6 = 72\ m^{2} [tex]
Volume: [tex] V = 3 \cdot 2^{2} \cdot 6 = 72\ m^{3} [tex]
[tex] \frac{A_{(L)}}{V} = \frac{72}{72} = 1 [tex]
Área lateral: [tex] A_{L} = 2 \cdot 3 \cdot 2 \cdot 8 = 96\ m^{2} [tex]
Volume: [tex] V = 3 \cdot 2^{2} \cdot 9 = 96\ m^{3} [tex]
[tex] \frac{A_{(L)}}{V} = \frac{96}{96} = 1 [tex]
Área lateral: [tex] A_{L} = 2 \cdot 3 \cdot 3 \cdot 8 = 144\ m^{2} [tex]
Volume: [tex] V = 3 \cdot 3^{2} \cdot 8 = 216\ m^{3} [tex]
[tex] \frac{A_{(L)}}{V} = \frac{144}{216} = \frac{2}{3} [tex]
Assim, o tanque escolhido deverá ser o tanque (III), por conta da relação igual a [tex] \frac{2}{3}[tex], que é o menor valor entre as relações disponíveis.
(ENEM 2010 - 1ª Aplicação).
Uma empresa possui um sistema de controle de qualidade que classifica o seu desempenho financeiro anual, tendo como base o do ano anterior. Os conceitos são:
insuficiente , quando o crescimento é menor que 1%;
regular , quando o crescimento é maior ou igual a 1% e menor que 5%;
bom , quando o crescimento é maior ou igual a 5% e menor que 10%;
ótimo , quando é maior ou igual a 10% e menor que 20%; e
excelente , quando é maior ou igual a 20%.
Essa empresa apresentou lucro de R$ 132 000,00 em 2008 e de R$ 145 000,00 em 2009.
De acordo com esse sistema de controle de qualidade, o desempenho financeiro dessa empresa no ano de 2009 deve ser considerado
(145 000 – 132 000) = 13 000
132 000 ----- 100%
13 000 ----- x%
[tex] x = \frac{13\ 000 \cdot\ 100}{132\ 000} = \frac{1\ 300}{132} = 9,8 \% [tex]
(ENEM 2010 - 1ª Aplicação).
Uma escola recebeu do governo uma verba de R$ 1000,00 para enviar dois tipos de folhetos pelo correio. O diretor da escola pesquisou que tipos de selos deveriam ser utilizados. Concluiu que, para o primeiro tipo de folheto, bastava um selo de R$ 0,65 enquanto para folhetos do segundo tipo seriam necessários três selos, um de R$ 0,65, um de R$ 0,60 e um de R$ 0,20. O diretor solicitou que se comprassem selos de modo que fossem postados exatamente 500 folhetos do segundo tipo e uma quantidade restante de selos que permitisse o envio do máximo possível de folhetos do primeiro tipo.
Quantos selos de R$ 0,65 foram comprados?
Para que fossem enviados 500 selos do segundo tipo, mais x selos do primeiro tipo, totalizando um valor igual ou inferior a R$ 1000,00, tem-se:
x∙(0,65) + 500(0,65 + 060 + 0,20) ≤ 1000
x ≤ 423,07
Logo, x = 423 selos primeiro tipo.
Assim, o total de selos de R$ 0,65 que foram comprados é de 923.
(ENEM 2010 - 1ª Aplicação).
A figura a seguir é a representação de uma região por meio de curvas de nível, que são curvas fechadas representando a altitude da região, com relação ao nível do mar. As coordenadas estão expressas em graus de acordo com a longitude, no eixo horizontal, e a latitude, no eixo vertical. A escala em tons de cinza desenhada à direita está associada à altitude da região.

Um pequeno helicóptero usado para reconhecimento sobrevoa a região a partir do ponto X = (20; 60). O helicóptero segue o percurso:
0,8°L → 0,5°N → 0,2° O → 0,1° S → 0,4° N → 0,3 °L
Ao final, desce verticalmente até pousar no solo.
De acordo com as orientações, o helicóptero pousou em um local cuja altitude é
Do enunciado, temos:

O percurso é dado pela poligonal que une os pontos X, A, B, C, D, E e F, como é mostrado na figura:

Assim, da escala de tons apresentada, podemos concluir que o helicóptero pousou num local cuja altitude é menor ou igual a 200 m.
(ENEM 2010 - 1ª Aplicação).
Para construir uma manilha de esgoto, um cilindro com 2 m de diâmetro e 4 m de altura (de espessura desprezível), foi envolvido homogeneamente por uma camada de concreto, contendo 20 cm de espessura.
Supondo que cada metro cúbico de concreto custe R$ 10,00 e tomando 3,1 como valor aproximado de π, então o preço dessa manilha é igual a
Calculando o volume (E) e o volume (F) do cilindro formado com a camada de concreto e realizando a diferença F – E tem-se o volume da manilha, que multiplicado por R$ 10,00 fornece o seu valor em R$:
E = 3,1 ∙ 1² ∙ 4 = 12,4
F = 3,1 ∙ (1,2)² ∙ 4 = 12,4 ∙ 1,44 = 17,856
Logo, F – E = 5,456 multiplicado por R$10,00, obtém-se R$ 54,56.
(ENEM 2010 - 1ª Aplicação).
No manejo sustentável de florestas, é preciso muitas vezes obter o volume da tora que pode ser obtida a partir de uma árvore. Para isso, existe um método prático, em que se mede a circunferência da árvore à altura do peito de um homem (1,30 m), conforme indicado na figura. A essa medida denomina-se "rodo" da árvore. O quadro a seguir indica a fórmula para se cubar, ou seja, obter o volume da tora em m3 a partir da medida do rodo e da altura da árvore.
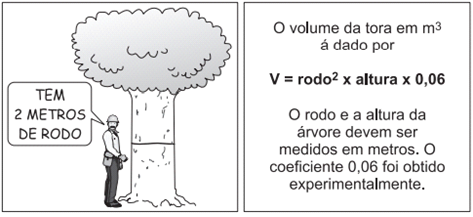
Um técnico em manejo florestal recebeu a missão de cubar, abater e transportar cinco toras de madeira, de duas espécies diferentes, sendo
• 3 toras da espécie I, com 3 m de rodo, 12 m de comprimento e densidade 0,77 toneladas/m³;
• 2 toras da espécie II, com 4 m de rodo, 10 m de comprimento e densidade 0,78 toneladas/m³.
Após realizar seus cálculos, o técnico solicitou que enviassem caminhões para transportar uma carga de, aproximadamente,
O primeiro passo é calcular o volume de cada espécie de árvore utilizando a expressão matemática dada no problema, tem-se:
Espécie I:
[tex] V_{I} = rodo^{2} \cdot altura \cdot 0,06 [tex]
[tex] V_{I} = 3^{2} \cdot 12 \cdot 0,06 = 6,48\ m^{3} [tex]
Como são três toras, temos:
[tex] V_{I} = 3 \cdot 6,48 = 19,44\ m^{3} [tex]
Espécie II:
[tex] V_{II} = rodo^{2} \cdot altura \cdot 0,06 [tex]
[tex] V_{II} = 4^{2} \cdot 10 \cdot 0,06 = 9,6\ m^{3} [tex]
Como são duas toras, temos:
[tex] V_{II} = 2 \cdot 9,6 = 19,2\ m^{3} [tex]
O segundo passo é calcular a massa total das toras e para isso se utiliza a densidade de cada espécie de tora, tem-se:
Espécie I:
[tex] d_{I} = \frac{m}{v} → m = 0,77 \cdot 19,44\ \cong 14,969 [tex] toneladas
Espécie II:
[tex] d_{II} = \frac{m}{v} → m = 0,78 \cdot 19,2\ \cong 14,976 [tex] toneladas
O terceiro e último passo é calcular a massa total das toras a serem transportadas pelos caminhões, tem-se:
[tex] m_{(total)} = 14,969 + 14,976 = 29,945 [tex] toneladas
Os caminhões devem suportar transportar um total aproximado de 29,9 toneladas.
(ENEM 2010 - 1ª Aplicação).
Embora o Índice de Massa Corporal (IMC) seja amplamente utilizado, existem ainda inúmeras restrições teóricas ao uso e às faixas de normalidade preconizadas.
O Recíproco do Índice Ponderal (RIP), de acordo com o modelo alométrico, possui uma melhor fundamentação matemática, já que a massa é uma variável de dimensões cúbicas e a altura, uma variável de dimensões lineares.
As fórmulas que determinam esses índices são:

ARAUJO. C. G. S.; RICARDO, D.R. Índice de Massa Corporal: Um Questionamento Cientifício Baseado em Evidências. Arq. Bras. Cardiologia, volume 79, n.o 1, 2002 (adaptado).
Se uma menina, com 64 kg de massa, apresenta IMC igual a 25 kg/m², então ela possui RIP igual a
Pela fórmula do IMC e com os dados fornecidos pela questão, é possível calcular a altura (h) da menina:
[tex] IMC = \frac{massa}{(altura)^{2}} → 25 = \frac{64}{(h)^{2}} [tex]
[tex] → h^{2} = \frac{64}{25} = 2,56 [tex]
[tex] → h = \sqrt{2,56} = 1,6\ m = 160\ cm [tex]
Sabendo agora o valor da altura h (em cm) da menina e o valor de sua massa, tem-se:
[tex] RIP = \frac{altura(cm)}{\sqrt[3]{massa\ (kg)}} [tex]
[tex] RIP = \frac{160}{\sqrt[3]{64}} = \frac{160}{4} = 40 [tex]
(ENEM 2010 - 1ª Aplicação).
Um balão atmosférico, lançado em Bauru (343 quilômetros a Noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista, na região de Presidente Prudente, assustando agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil, França, Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu após o cumprimento do tempo previsto de medição.
Disponível em: http://www.correiodobrasil.com.br. Acesso em: 02 maio 2010.

Na data do acontecido, duas pessoas avistaram o balão.
Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60°; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30°.
Qual a altura aproximada em que se encontrava o balão?
Para resolver essa questão, basta calcular a tangente do ângulo de 60°. Lembrando que a tangente é o quociente do lado oposto pelo lado adjacente ao ângulo.
O valor da medida do lado adjacente está na figura da questão, 1,8 km. A medida do lado oposto ao ângulo de 60° é o valor que estamos procurando e pode ser chamada de h.
Na tabela trigonométrica, podemos ver que a tangente de 60° vale [tex]\sqrt{3} [tex]. Façamos então:
[tex] tg 60° = \frac{cateto\ oposto\ a\ 60°}{cateto\ adjacente\ a\ 60°}[tex]
[tex] \sqrt{3} = \frac{h}{1,8} [tex]
[tex] h = 1,8 \cdot 1,73\ \cong\ 3,114\ km [tex]
A alternativa correta é aquela que mais se aproxima do resultado encontrado, portanto, a letra C.
(ENEM 2010 - 1ª Aplicação).
Em canteiros de obras de construção civil é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo, conforme pode ser visto na figura, em que as estacas foram indicadas por letras.

A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto.
Nessas condições, a área a ser calçada corresponde
Existe uma semelhança entre os triângulos BAC e MNC, K = 2 e a razão entre suas áreas é igual a k² = 4. Portanto, sendo S a área do triangulo MNC e C igual a região que deveria ser calçada com concreto, tem-se: = k² que corresponde a C + S = 4S = C + 3S.
Logo, a área que deveria ser calçada é o triplo da área do triângulo MNC.
(ENEM 2010 - 1ª Aplicação).
O jornal de certa cidade publicou em uma página inteira a seguinte divulgação de seu caderno de classificados.

Para que a propaganda seja fidedigna à porcentagem da área que aparece na divulgação, a medida do lado do retângulo que representa os 4%, deve ser de aproximadamente
Para a propaganda ser fidedigna à porcentagem de área permitida, o jornal terá que fazer com que o lado x multiplicado pelos 26 mm dado pela questão, corresponda a 4% da área da página inteira e estabeleça as condições impostas pela questão, logo:
[tex] 26 \cdot x = \frac{4}{100} \cdot (260 \cdot 400) [tex]
[tex] x = 160\ mm [tex]
(ENEM 2010 - 1ª Aplicação).
A ideia de usar rolos circulares para deslocar objetos pesados provavelmente surgiu com os antigos egípcios ao construírem as pirâmides.

Representando por R o raio da base dos rolos cilíndricos, em metros, a expressão do deslocamento horizontal y do bloco de pedra em função de R, após o rolo ter dado uma volta completa sem deslizar, é
Considerando o rolo como um cilindro perfeito, este tem como base uma circunferência. Uma volta completa do rolo é como se esticar a circunferência da base do rolo, vê-se:

O comprimento da circunferência é dado por:
C = 2πR
Fique atento, enquanto o rolo dá uma volta sobre o solo, o bloco corre sobre o rolo a mesma distância da volta, vê-se:

Sendo assim, o bloco se deslocou por dois comprimentos da circunferência, tem-se:
D = 2C = 2 . 2πR = 4πR
(ENEM 2010 - 1ª Aplicação).
Uma metalúrgica recebeu uma encomenda para fabricar, em grande quantidade, uma peça com o formato de um prisma reto com base triangular, cujas dimensões da base são 6 cm, 8 cm e 10 cm e cuja altura é 10 cm. Tal peça deve ser vazada de tal maneira que a perfuração na forma de um cilindro circular reto seja tangente às suas faces laterais, conforme mostra a figura.

O raio da perfuração da peça é igual a
Seja r o raio da base do cilindro. O triângulo é retângulo, pois [tex]6^{2} + 8^{2} = 10^{2}[tex].
Logo, sua área será:
[tex] A = \frac{b\ \cdot\ h}{2} = \frac{6\ \cdot\ 8}{2} = 24 [tex]

Portanto,
[tex] \frac{6\ \cdot\ r}{2} + \frac{8\ \cdot\ r}{2} + \frac{10\ \cdot\ r}{2} = 24 [tex]
[tex] 24r = 48 [tex]
[tex] r = 2 [tex]
(ENEM 2010 - 1ª Aplicação).
Nos processos industriais, como na indústria de cerâmica, é necessário o uso de fornos capazes de produzir elevadas temperaturas e, em muitas situações, o tempo de elevação dessa temperatura deve ser controlado, para garantir a qualidade do produto final e a economia no processo.
Em uma indústria de cerâmica, o forno é programado para elevar a temperatura ao longo do tempo de acordo com a função.

em que T é o valor da temperatura atingida pelo forno, em graus Celsius, e t é o tempo, em minutos, decorrido desde o instante em que o forno é ligado.
Uma peça deve ser colocada nesse forno quando a temperatura for 48°C e retirada quando a temperatura for 200°C.
O tempo de permanência dessa peça no forno é, em minutos, igual a
Vemos que, quando uma peça for colocada no forno a uma temperatura de 48ºC, teremos:
T(t) = 75t + 20
48 = 75t + 20
t = 20 min
E também, quando for retirada do forno a uma temperatura de 200ºC, teremos:
T(t) = 2125t² − 165t + 320
200 = 2125t² − 165t + 320
t² – 200t + 7 500 = 0
Agora, resolvendo a equação, obtemos:
a = 1, b = -200, c = 7500
[tex] Δ = b² - 4ac = (-200)² - 4 . 1 . 7500 = 10 000[tex]
[tex] t = \frac{-b \pm \sqrt{ Δ }}{2a} = \frac{-(-200) \pm \sqrt{ 10\ 000 }}{2 \cdot 1} [tex]
[tex] t = \frac{200) \pm 100}{2} [tex]
[tex] t' = \frac{200) + 100}{2} = 150 [tex]
[tex] t'' = \frac{200) - 100}{2} = 50 [tex]
Assim, t = 150 minutos.
Portanto, o tempo de permanência dessa peça no forno é de 150 – 20 = 130 minutos.
(ENEM 2010 - 1ª Aplicação).
O gráfico mostra o número de favelas no município do Rio de Janeiro entre 1980 e 2004, considerando que a variação nesse número entre os anos considerados é linear.

Favela Tem Memória. Época. N.o 621, 12 abr. 2010 (adaptado).
Se o padrão na variação do período 2004/2010 se mantiver nos próximos 6 anos, e sabendo que o número de favelas em 2010 é 968, então o número de favelas em 2016 será
Sendo o padrão de variação de 2004/2010 igual a 968 – 750 = 218 e que o padrão de 2010/2016 se manteve igual ao de 2004/2010, ou seja, 218.
Como o enunciado nos propõe que o número de favelas em 2010 é de 968, logo o número de favelas em 2016 será de 968 + 218 = 1186 favelas.
(ENEM 2010 - 1ª Aplicação).
O gráfico apresenta a quantidade de gols marcados pelos artilheiros das Copas do Mundo desde a Copa de 1930 até a de 2006.
Quantidades de Gols dos Artilheiros das Copas do Mundo

Disponível em: http://www.suapesquisa.com. Acesso em: 23 abr. 2010 (adaptado).
A partir dos dados apresentados, qual a mediana das quantidades de gols marcados pelos artilheiros das Copas do Mundo?
Sendo 8; 5; 7; 9; 11; 13; 4; 9; 10; 7; 6; 6; 6; 6; 6; 6; 8; 5 os dados apresentados pelo gráfico da questão. Agora, colocando-os em ordem obtém-se o ROL dos gol marcados pelos artilheiros das copas do Mundo.
(4; 5; 5; 6; 6; 6; 6; 6; 6; 7; 7; 8; 8; 9; 9; 10; 11; 13)
e pegando os dois elementos centrais desse ROL e fazendo uma média aritmética simples, obtém-se a mediana que é:
[tex] M = \frac{6+7}{2} = 6,5 [tex]
(ENEM 2010 - 1ª Aplicação).
Em um casamento, os donos da festa serviam champanhe aos seus convidados em taças com formato de um hemisfério (Figura 1), porém um acidente na cozinha culminou na quebra de grande parte desses recipientes.
Para substituir as taças quebradas, utilizou-se um outro tipo com formato de cone (Figura 2). No entanto, os noivos solicitaram que o volume de champanhe nos dois tipos de taças fosse igual.

Sabendo que a taça com o formato de hemisfério é servida completamente cheia, a altura do volume de champanhe que deve ser colocado na outra taça, em centímetros, é de
Note que os noivos solicitaram que o volume entre as duas taças seja o mesmo, portanto devemos explicitar a relação entre o volume das taças, de modo a conseguir determinar o valor da altura que fará com que o volume da taça em formato de hemisfério seja igual ao da taça de formato de cone.
Foi-nos informada a expressão dos volumes da esfera e do cone, entretanto, a taça não é uma esfera completa e sim “metade” de uma esfera, portanto devemos determinar uma expressão para o volume da Figura 1.
[tex] V_{(hemisfério)} = \frac{1}{2} \cdot V_{(esfera)} [tex]
[tex] = \frac{2}{3} \cdot π \cdot R^{3} [tex]
Devemos ter o volume do hemisfério igual ao volume da figura 2, portanto:
[tex] \frac{2}{3} \cdot π \cdot R^{3} = \frac{1}{3} \cdot π \cdot R^{2} \cdot h [tex]
Após substituirmos os dados que o exercício nos deu, veremos que só nos falta o valor da altura, que é justamente a medida que determinará a relação de igualdade entre as duas taças.
[tex] \frac{2}{3} \cdot π \cdot 3^{3} = \frac{1}{3} \cdot π \cdot 3^{2} \cdot h [tex]
[tex] h = 6 [tex]
(ENEM 2010 - 1ª Aplicação).
O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado.
Disponível em: www.cbat.org.br (adaptado).
Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m. Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre
Sendo x o valor do primeiro salto, (x – 1,2) será o valor do segundo salto e (x – 2,7) o valor do terceiro salto, logo para que o atleta alcance a meta de 17,4m no salto triplo
x + (x – 1,2) + (x – 2,7)
terá que ser igual a 17,4, tem-se:
x + (x – 1,2) + (x – 2,7) = 17,4
x = 7,1 m
Logo, considerando os seus estudos, terá que alcançar 7,1 m no primeiro salto para atingir a meta de 17,4 m.
(ENEM 2010 - 1ª Aplicação).
Marco e Paulo foram classificados em um concurso. Para a classificação no concurso o candidato deveria obter média aritmética na pontuação igual ou superior a 14. Em caso de empate na média, o desempate seria em favor da pontuação mais regular. No quadro a seguir são apresentados os pontos obtidos nas provas de Matemática, Português e Conhecimentos Gerais, a média, a mediana e o desvio padrão dos dois candidatos.
Dados dos candidatos no concurso

O candidato com pontuação mais regular, portanto mais bem classificado no concurso, é
As médias de Marco e Paulo são iguais, mas o desvio padrão de Marco é menor, o que significa que suas notas nas provas estão mais próximas da média do que as notas de Paulo.
Portanto, as notas obtidas por Marco no concurso são mais regulares, logo Marco foi melhor classificado.
(ENEM 2010 - 1ª Aplicação).
Um grupo de pacientes com Hepatite C foi submetido a um tratamento tradicional em que 40% desses pacientes foram completamente curados. Os pacientes que não obtiveram cura foram distribuídos em dois grupos de mesma quantidade e submetidos a dois tratamentos inovadores. No primeiro tratamento inovador, 35% dos pacientes foram curados e, no segundo, 45%.
Em relação aos pacientes submetidos inicialmente, os tratamentos inovadores proporcionaram cura de
Supondo ser 100 o número de pacientes e que 60% não foram completamente curados. Logo, 60 pacientes não foram completamente curados, dividindo os 60 em dois grupos de 30, e no primeiro grupo com o primeiro tratamento inovador 35% dos pacientes foram curados, ou seja, 10,5 pacientes curados, no segundo grupo 45% foram curados, ou seja, 13,5 foram curados.
Portanto, somando os 10,5 curados do primeiro grupo com os 13,5 curados do segundo grupo, obtém-se um total de 24 curados com tratamentos inovadores, num grupo inicial de supostamente 100 pacientes.
Logo, 24%.
(ENEM 2010 - 1ª Aplicação).
Em 2006, a produção mundial de etanol foi de 40 bilhões de litros e a de biodiesel, de 6,5 bilhões.
Neste mesmo ano, a produção brasileira de etanol correspondeu a 43 % da produção mundial, ao passo que a produção dos Estados Unidos da América, usando milho, foi de 45%.
Disponível em: planetasustentavel.abril.com.br. Acesso em: 02 maio 2009.
Considerando que, em 2009, a produção mundial de etanol seja a mesma de 2006 e que os Estados Unidos produzirão somente a metade de sua produção de 2006, para que o total produzido pelo Brasil e pelos Estados Unidos continue correspondendo a 88% da produção mundial, o Brasil deve aumentar sua produção em, aproximadamente,
No enunciado verificamos que a produção mundial de etanol foi de 40 bilhões de litros. Observe que 43% dessa produção corresponde ao Brasil e 45% aos Estados Unidos.
BRASIL: [tex] \frac{43}{100} \cdot 40\ bilhões = 17,2\ bilhões [tex]
EUA: [tex] \frac{45}{100} \cdot 40\ bilhões = 18\ bilhões [tex]
Juntos, Brasil e EUA produziram em 2006: 17,2 + 18 = 35,2 bilhões de litros de etanol.
Portanto, em 2006, o Brasil e os Estados Unidos produziram 35,2 bilhões de litros de etanol.
Agora vamos verificar no ano de 2009:
EUA: a produção de etanol caiu pela metade = [tex] \frac{18}{2} = 9\ [tex] bilhões de litros.
Para continuar com a mesma porcentagem da produção mundial, a produção do Brasil deverá compensar a redução dos EUA, ou seja, aumentar 9 bilhões.
Vamos montar a Regra de Três Simples para descobrir o percentual de aumento da produção Brasileira de etanol.
17,2 litros ---- 100 %
9 litros ----- x %
[tex] x = \frac{9\ \cdot\ 100}{17,2} = \frac{900}{17,2} [tex]
[tex] x \cong 52,32 \% [tex]
(ENEM 2010 - 1ª Aplicação).
João mora na cidade A e precisa visitar cinco clientes, localizados em cidades diferentes da sua. Cada trajeto possível pode ser representado por uma sequência de 7 letras. Por exemplo, o trajeto ABCDEFA, informa que ele sairá da cidade A, visitando as cidades B, C, D, E e F nesta ordem, voltando para a cidade A. Além disso, o número indicado entre as letras informa o custo do deslocamento entre as cidades. A figura mostra o custo de deslocamento entre cada uma das cidades.

Como João quer economizar, ele precisa determinar qual o trajeto de menor custo para visitar os cinco clientes.
Examinando a figura, percebe que precisa considerar somente parte das sequências, pois os trajetos ABCDEFA e AFEDCBA têm o mesmo custo. Ele gasta 1 min30s para examinar uma sequência e descartar sua simétrica, conforme apresentado.
O tempo mínimo necessário para João verificar todas as sequências possíveis no problema é de
As possibilidades de João efetuar as visitas são iguais a [tex] \frac{5!}{2} = \frac{120}{2} = 60 [tex] , que é o total de possibilidades descartando as simétricas.
Como a questão fornece que João gasta 90 segundos (1min30seg) para cada sequência. Logo, o tempo mínimo necessário é de:
60 × 90 segundos = 5400 segundos (90min).
(ENEM 2010 - 1ª Aplicação).
O diretor de um colégio leu numa revista que os pés das mulheres estavam aumentando. Há alguns anos, a média do tamanho dos calçados das mulheres era de 35,5 e, hoje, é de 37,0. Embora não fosse uma informação científica, ele ficou curioso e fez uma pesquisa com as funcionárias do seu colégio, obtendo o quadro a seguir:
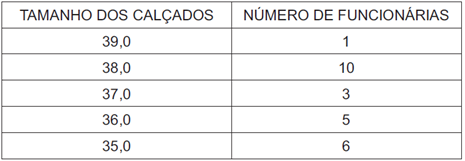
Escolhendo uma funcionária ao acaso e sabendo que ela tem calçado maior que 36,0, a probabilidade de ela calçar 38,0 é
Observando a tabela, tem-se que o número de funcionários com calçado maior que 36,6 é igual a 1 + 10 + 3 =14, dos quais 10 funcionários calçam 38,0.
Logo, tendo escolhido ao acaso um funcionário que calce mais de 38,0 a probabilidade dela calçar 38,0 é de
[tex] P = \frac{10}{14} = \frac{5}{7} [tex]
(ENEM 2010 - 1ª Aplicação).
O quadro seguinte mostra o desempenho de um time de futebol no último campeonato. A coluna da esquerda mostra o número de gols marcados e a coluna da direita informa em quantos jogos o time marcou aquele número de gols.

Se X, Y e Z são, respectivamente, a média, a mediana e a moda desta distribuição, então
A média X de gols por partida é:
[tex] X = \frac{0 \cdot 5 + 1 \cdot 3 + 2 \cdot 4 + 3 \cdot 3 + 4 \cdot 2 + 5 \cdot 2 + 7 \cdot 1 }{20} [tex]
[tex] X = \frac{45}{20} = 2,25 [tex]
No rol dos gols marcados por partida, a mediana Y é a média entre os gols marcados nas 10ª e 11ª partidas. Assim:
[tex] Y = \frac{2+2}{2} = 2 [tex]
A moda Z dos gols marcados é: Z = 0.
Logo, Z < Y < X.
(ENEM 2010 - 1ª Aplicação).
A disparidade de volume entre os planetas é tão grande que seria possível colocá-los uns dentro dos outros. O planeta Mercúrio é o menor de todos. Marte é o segundo menor: dentro dele cabem três Mercúrios. Terra é o único com vida: dentro dela cabem sete Martes. Netuno é o quarto maior: dentro dele cabem 58 Terras. Júpiter é o maior dos planetas: dentro dele cabem 23 Netunos.
Revista Veja. Ano 41, nº 25, 25 jun. 2008 (adaptado).
Seguindo o raciocínio proposto, quantas Terras cabem dentro de Júpiter?
Do enunciado, temos a relação volumétrica que pode ser representada pela tabela:
1 Marte = 3 Mercúrios
1 Terra = 7 Martes
1 Netuno = 58 Terras
1 Júpiter = 23 Netunos
Assim sendo, temos que, para cada Netuno que cabe em Júpiter, caberão 58 Terras.
Se em Júpiter cabem 23 Netunos, o número de Terras que nele cabem, é: 58 × 23 = 1334.
(ENEM 2010 - 1ª Aplicação).
Um dos grandes problemas da poluição dos mananciais (rios, córregos e outros) ocorre pelo hábito de jogar óleo utilizado em frituras nos encanamentos que estão interligados com o sistema de esgoto. Se isso ocorrer, cada 10 litros de óleo poderão contaminar 10 milhões (10⁷) de litros de água potável.
Manual de etiqueta. Parte integrante das revistas Veja (ed. 2055), Cláudia (ed. 555), National Geographic (ed. 93) e Nova Escola (ed. 208) (adaptado).
Suponha que todas as famílias de uma cidade descartem os óleos de frituras através dos encanamentos e consomem 1 000 litros de óleo em frituras por semana.
Qual seria, em litros, a quantidade de água potável contaminada por semana nessa cidade?
Sendo x a quantidade, em litros, de água contaminada, nas condições dadas temos:
10 litros de óleo ----- 10 milhões (10⁷) litros de água
10³ litros de óleo ----- x litros de água
[tex] x = \frac{10^{7}\ \cdot\ 10^{3}}{10} = 10^{9} [tex]
(ENEM 2010 - 1ª Aplicação).
Um porta-lápis de madeira foi construído no formato cúbico, seguindo o modelo ilustrado a seguir. O cubo de dentro é vazio. A aresta do cubo maior mede 12 cm e a do cubo menor, que é interno, mede 8 cm.

O volume de madeira utilizado na confecção desse objeto foi de
O volume do cubo externo subtraído o volume do cubo interno é igual ao volume de madeira utilizado na confecção desse objeto, logo, tem-se que o volume de madeira utilizado na confecção foi de:
[tex]V_{(cubo\ maior)} – V_{(cubo\ menor)} = 12^{3} – 8^{3} = 1\ 216\ cm^{3} [tex]
(ENEM 2010 - 1ª Aplicação).
Ronaldo é um garoto que adora brincar com números.
Numa dessas brincadeiras, empilhou caixas numeradas de acordo com a sequência conforme mostrada no esquema a seguir.

Ele percebeu que a soma dos números em cada linha tinha uma propriedade e que, por meio dessa propriedade, era possível prever a soma de qualquer linha posterior às já construídas.
A partir dessa propriedade, qual será a soma da 9ª linha da sequência de caixas empilhadas por Ronaldo?
A propriedade percebida foi
[tex] S_{n} = 2 \cdot (1 + n)\cdot (– n) = n² [tex]
Logo, a 9ª linha da sequência de caixa é
S = 9² = 81
(ENEM 2010 - 1ª Aplicação).
Para conseguir chegar a um número recorde de produção de ovos de Páscoa, as empresas brasileiras começam a se planejar para esse período com um ano de antecedência.
O gráfico a seguir mostra o número de ovos de Páscoa produzidos no Brasil no período de 2005 a 2009.

Revista Veja. São Paulo: Abril, ed. 2107, n.o 14, ano 42.
De acordo com o gráfico, o biênio que apresentou maior produção acumulada foi
Tomando por base somente os dados apresentados na questão. O biênio que apresentou maior produção acumulada foi:
2008-2009, pois teve uma produção acumulada de (107 + 113) = 220 milhões de ovos de páscoa.
Enquanto:
2005-2006: (90 + 94) = 184 milhões de ovos.
2006-2007: (94 + 99) = 193 milhões de ovos.
2007-2008: (107 + 99) = 206 milhões de ovos.

Nenhum comentário:
Postar um comentário