(ENEM 2014 - 2ª Aplicação).
Em uma escola, cinco atletas disputam a medalha de ouro em uma competição de salto em distância. Segundo o regulamento dessa competição, a medalha de ouro será dada ao atleta mais regular em uma série de três saltos.
Os resultados e as informações dos saltos desses cinco atletas estão no quadro.

A medalha de ouro foi conquistada pelo atleta número
Pelos dados do gráfico e do texto, conclui-se que o atleta III é o mais regular pois, possui o desvio padrão menor, ou seja, 0,17.
(ENEM 2014 - 2ª Aplicação).
A figura é uma representação tridimensional da molécula do hexaflureto de enxofre, que tem a forma bipiramidal quadrada, na qual o átomo central de enxofre está cercado por sei átomos de flúor, situados nos seis vértices de um octaedro. O ângulo entre qualquer par de ligações enxofre-flúor adjacentes mede 90°.

A vista superior da molécula, como representada na figura, é:

Na projeção, o átomo de flúor superior e inferior fica sobreposto e o átomo de Enxofre é maior do que o de flúor. Logo, a alternativa B é a correta.
(ENEM 2014 - 2ª Aplicação).
Corta-se um cubo ABCDEFGH por um plano ortogonal às faces ABCD e EFGH que contém os pontos médios I e J das arestas CD e BC e elimina-se, em seguida, o prisma IJCLKG, obtendo-se o prisma ABJIDEFKLH.

A planificação da superfície do prisma resultante ABJIDEFKLH corresponde à figura
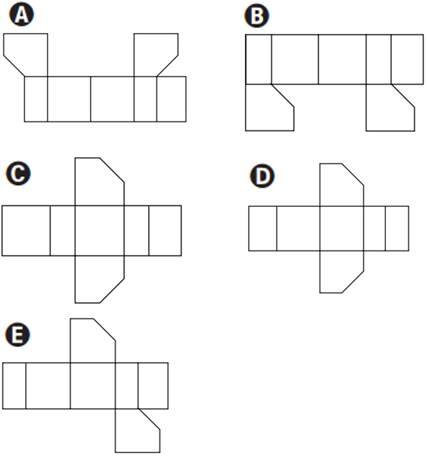
Veja o esquema a seguir.

Logo, opção E.
(ENEM 2014 - 2ª Aplicação).
Após encerrar o período de vendas de 2012, uma concessionária fez um levantamento das vendas de carros novos no último semestre desse ano. Os dados estão expressos no gráfico:

Ao fazer a apresentação dos dados aos funcionários, o gerente estipulou como meta para o mês de janeiro de 2013 um volume de vendas 20% superior à média mensal de vendas do semestre anterior.
Para atingir essa meta, a quantidade mínima de carros que deveriam ser vendidos em janeiro de 2013 seria
Primeiro vamos encontrar o total de carros vendidos. Essa informação encontra-se diretamente no gráfico.
Total de carros = 5 + 6 + 14 + 35 + 35 + 25 = 120
Como para atingir a meta terá que aumentar as vendas em 20%.
Logo,
120 × 20% = 120 × 0,2 = 24 carros.
(ENEM 2014 - 2ª Aplicação).
Uma loja decide premiar seus clientes. Cada cliente receberá um dos seis possíveis brindes disponíveis, conforme sua ordem de chegada na loja. Os brindes a serem distribuídos são: uma bola, um chaveiro, uma caneta, um refrigerante, um sorvete e um CD, nessa ordem. O primeiro cliente da loja recebe uma bola, o segundo recebe um chaveiro, o terceiro recebe uma caneta, o quarto recebe um refrigerante, o quinto recebe um sorvete, o sexto recebe um CD, o sétimo recebe uma bola, o oitavo recebe um chaveiro, e assim sucessivamente, segundo a ordem dos brindes.
O milésimo cliente receberá de brinde um(a)
Como os brindes segue a sequência. Assim, temos:
1°. cliente: bola
2°. cliente: chaveiro
3°. cliente: canivete
4°. cliente: refrigerante
5°. cliente: sorvete
6°. cliente: CD
7°. cliente: bola
8°. cliente: chaveiro
⁞ ⁞
1000°. cliente: ????
Como o sorteio dos brindes segue esta ordem. Logo,

Assim, terá feito 166 ciclo de sorteio completos e ainda sobrará 4 brindes. Assim, procedendo da mesma forma anterior para esses quatro últimos brindes, obtemos:
1°. cliente: bola
2°. cliente: chaveiro
3°. cliente: canivete
4°. cliente: refrigerante
Portanto, o 1000° cliente receberá um refrigerante como brinde.
(ENEM 2014 - 2ª Aplicação).
O ferro é um mineral fundamental para que as células mantenham seu bom funcionamento. Ele é essencial ao transporte de oxigênio, síntese de DNA e metabolismo energético. É recomendado para meninos de 9 a 13 anos ingerirem, pelo menos, 8 mg de ferro por dia.
Pesquisadores elaboraram a tabela com alguns alimentos e as suas respectivas quantidades de ferro:

A diretora de uma escola sabe que deve escolher para o almoço de seus alunos o máximo de cardápios possíveis entre três cardápios existentes, no(s) qual(is) cada porção equivale a 100 g e cada copo a 50 g.

Disponível em: www.rgnutri.com.br. Acesso em: 2 ago (adaptado).
Para ter certeza de que seus alunos estão ingerindo a quantidade mínima de ferro recomendada, a diretora deve escolher o(s) cardápio(s)
Como a diretora que saber qual é o cardápio que satisfaz a quantidade mínima de ferro por dia, ou seja, 8 mg por dia.
Logo, temos:
Cardápio 1:
2 porções de feijão carioca = 2 × 1,3 = 2,6 mg
1 porção de coração de frango = 6,5 mg → Total: 2,6 + 6,5 + 3,1 = 12,2 mg
1 porção de amêndoa = 3,1 mg
Cardápio 2:
2 copos de caldo de cana = 2 × 2,3 = 4,6 mg
1 porção de sardinha em conserva = 3,5 mg → Total: 4,6 + 3,5 + 2,6 = 10,7 mg
2 porções de feijão carioca = 2 × 1,3 = 2,6 mg
Cardápio 3:
2 porções de lentilha = 2 × 1,5 = 3,0 mg
3 porções de filé de frango = 3 × 0,3 = 0,9 mg → Total: 3,0 + 0,9 + 3,0 = 6,9 mg
2 porções de batata doce = 2 × 1,5 = 3,0 mg
Assim, os cardápios que satisfazem as necessidades mínimas de ferro diárias são os cardápios 1 e 2.
(ENEM 2014 - 2ª Aplicação).
Um estudante se cadastrou numa rede social na internet que exibe o índice de popularidade do usuário. Esse índice é a razão entre o número de admiradores do usuário e o número de pessoas que visitam seu perfil na rede.
Ao acessar seu perfil hoje, o estudante descobriu que seu índice de popularidade é 0,312121212....
O índice revela que as quantidades relativas de admiradores do estudante e pessoas que visitam seu perfil são
Para obter este índice é necessário encontrar a geratriz. Logo, tomamos:
x = 0,312121212....
Subtraindo o produto por 1000 e por 10 a igualdade acima, obtemos:

(ENEM 2014 - 2ª Aplicação).
Uma fábrica de rapadura vende seus produtos empacotados em uma caixa com as seguintes dimensões: 25 cm de comprimento; 10 cm de altura e 15 cm de profundidade. O lote mínimo de rapaduras vendido pela fábrica é um agrupamento de 125 caixas dispostas conforme a figura.

Qual é o volume do lote mínimo comercializado pela fábrica de rapaduras?
Primeiro vamos encontrar a capacidade de uma rapadura que tem dimensões: 25 cm de comprimento, 10 cm de altura e 15 cm de profundidade.
Logo,
V = 25 × 10 × 15 = 3 750 cm³
Como o lote é vendido em 125 caixas. Logo,
125 × 3 750 cm³ = 468 750 cm³
(ENEM 2014 - 2ª Aplicação).
Uma concessionária de automóveis revende atualmente três marcas de veículos, A, B e C, que são responsáveis por 50%, 30% e 20%, respectivamente, de sua arrecadação. Atualmente, o faturamento médio mensal dessa empresa é de R$ 150 000,00. A direção dessa empresa estima que, após uma campanha publicitária a ser realizada, ocorrerá uma elevação de 20%, 30% e 10% na arrecadação com as marcas A, B e C, respectivamente.
Se os resultados estimados na arrecadação forem alcançados, o faturamento médio mensal da empresa passará a ser de
Antes da campanha publicitária:
50% × 150 000,00 = 0,5 × 150 000,00 = 75 000,00
30% × 150 000,00 = 0,3 × 150 000,00 = 45 000,00
20% × 150 000,00 = 0,2 × 150 000,00 = 30 000,00
Agora, depois da campanha publicitária:
20% × 75 000,00 = 1,2 × 75 000,00 = 90 000,00
30% × 45 000,00 = 1,3 × 45 000,00 = 58 500,00
10% × 30 000,00 = 1,1 × 30 000,00 = 33 000,00
Por final, o faturamento passará para:
90 000 + 58 500 + 33 000 = 181 500,00
(ENEM 2014 - 2ª Aplicação).
Um lojista adquiriu novas embalagens para presentes que serão distribuídas aos seus clientes.
As embalagens foram entregues para serem montadas e têm forma dada pela figura.

Após montadas, as embalagens formarão um sólido com quantas arestas?
Na planificação, obtemos:
Faces: 7 (2 bases e 5 faces laterais)
Vértices: 10 (5 na base inferior e 5 na base superior)
Então, pela relação de Euler, obtemos:
F + V = A + 2
7 + 10 = A + 2
A = 15
(ENEM 2014 - 2ª Aplicação).
Um homem, determinado a melhorar sua saúde, resolveu andar diariamente numa praça circular que há em frente à sua casa. Todos os dias ele dá exatamente 15 voltas em torno da praça, que tem 50 m de raio.
Use 3 como aproximação para π.
Qual é a distância percorrida por esse homem em sua caminhada diária?
A distância percorrida será o valor de 15 voltas completas. Logo,
Distância percorrida = 2 × π × R × 15 = 2 × 3 × 50 × 15 = 4 500 m = 4,50 km.
(ENEM 2014 - 2ª Aplicação).
Enquanto as lâmpadas comuns têm 8 mil horas de vida útil, as lâmpadas LED têm 50 mil horas.
MetroCuritiba, 18 ago. 2011 (adaptado).
De acordo com a informação e desprezando possíveis algarismos na parte decimal, a lâmpada LED tem uma durabilidade de
Lâmpadas comuns:
[tex] \frac{8000\ h}{24\ h} = 333,3333 .... [tex]
Lâmpadas LED:
[tex] \frac{50\ 000\ h}{24\ h} = 2\ 083,3333 .... [tex]
Logo,
[tex] 2\ 083,3333 ... -\ 333,3333 .... = 1\ 750 [tex]
(ENEM 2014 - 2ª Aplicação).
Um construtor pretende murar um terreno e, para isso, precisa calcular o seu perímetro. O terreno está representado no plano cartesiano, conforme a figura, no qual foi usada a escala 1 : 500.
Use 2,8 como aproximação para [tex]\sqrt{8}[tex].

De acordo com essas informações, o perímetro do terreno, em metros, é
Primeiro vamos encontrar o perímetro do terreno:

[tex] P = 8 + 5 + 6 + \sqrt{8} + 3 [tex]
[tex] P = 8 + 5 + 6 + 2,8 + 3 = 24,8 cm [tex]
Agora, utilizando a escala 1 : 500 para obter o perímetro do perímetro.
1cm ----- (500 cm = 5m)
24,8 cm ---- x
x = 124 m
(ENEM 2014 - 2ª Aplicação).
A probabilidade de um empregado permanecer em uma dada empresa particular por 10 anos ou mais é de 1/6.
Um homem e uma mulher começam a trabalhar nessa companhia no mesmo dia. Suponha que não haja nenhuma relação entre o trabalho dele e o dela, de modo que seus tempos de permanência na firma são independentes entre si.
A probabilidade de ambos, homem e mulher, permanecerem nessa empresa por menos de 10 anos é de
Como foi informado no texto, a probabilidade de permanecer por mais de 10 anos: [tex]\frac{1}{6}[tex].
Então, a Probabilidade de permanecer por menos de 10 anos: [tex]\frac{5}{6}[tex].
Como, este homem e mulher começam a trabalhar no mesmo dia e que não haja nenhuma relação entre o trabalho dele e o dela, de modo que seus tempos de permanência na firma são independentes entre si.
Logo, a probabilidade deste homem e desta mulher permanecer por menos de 10 anos será:
[tex]\frac{5}{6} \cdot \frac{5}{6} = \frac{25}{36} [tex]
(ENEM 2014 - 2ª Aplicação).
O criador de uma espécie de peixe tem sete tanques, sendo que cada tanque contém 14 600 litros de água.
Nesses tanques, existem em média cinco peixes para cada metro cúbico (m³) de água. Sabe-se que cada peixe consome 1 litro de ração por semana. O criador quer construir um silo que armazenará a ração para alimentar sua criação.
Qual é a capacidade mínima do silo, em litros, para armazenar a quantidade de ração que garantirá a alimentação semanal dos peixes?
Dados:
* 7 tanques
* Volume de 1 tanque: 14 600 litros = 14,6 m².
* 5 peixes por m³
* 1 peixe consome 1 litro de razão por semana.
Assim,
Volume total dos tanques = 7 × 14,6 m³ = 102,2 m³
Agora, encontrar a quantidade de peixes:
Q(Peixes) = 5 peixes × 102,2 m³ = 511 peixes/m³
Como cada peixe consome 1 litro de razão por semana.
Portanto, serão necessários 511 litros de razão semanal.
(ENEM 2014 - 2ª Aplicação).
Um agricultor possui em sua fazenda um silo para armazenar sua produção de milho. O silo, que na época da colheita é utilizado em sua capacidade máxima, tem a forma de um paralelepípedo retângulo reto, com os lados da base medindo L metros e altura igual a h metros. O agricultor deseja duplicar a sua produção para o próximo ano e, para isso, irá comprar um novo silo, no mesmo formato e com o dobro da capacidade do atual. O fornecedor de silos enviou uma lista com os tipos disponíveis e cujas dimensões são apresentadas na tabela:

Para atender às suas necessidades, o agricultor deverá escolher o silo de tipo
Silo atual:

[tex]Silo_{(atual)}: V = L × L × h = L^{2} × h [tex]
Novo Silo:
[tex] Silo_{(I)} = L^{2} \cdot h = L^{2} \cdot 2h = 2(L^{2}h) = 2 \cdot (silo_{(atual)}) [tex]
[tex] Silo_{(II)} = L^{2} \cdot h = (2L)^{2} \cdot h = 4(L^{2}h) = 4 \cdot (silo_{(atual)}) [tex]
[tex] Silo_{(III)} = L^{2} \cdot h = (2L)^{2} \cdot 2h = 8(L^{2}h) = 8 \cdot (silo_{(atual)}) [tex]
[tex] Silo_{(IV)} = L^{2} \cdot h = (4L)^{2} \cdot h = 16(L^{2}h) = 16 \cdot (silo_{(atual)}) [tex]
[tex] Silo_{(V)} = L^{2} \cdot h = (L)^{2} \cdot 4h = 4(L^{2}h) = 4 \cdot (silo_{(atual)}) [tex]
Como o agricultor quer duplicar a capacidade de seu silo. Logo, o tipo mais adequado é o [tex]Silo_{(I)}[tex].
(ENEM 2014 - 2ª Aplicação).
Um construtor precisa revestir o piso de uma sala retangular. Para essa tarefa, ele dispõe de dois tipos de cerâmicas:
a) cerâmica em forma de quadrado de lado 20 cm, que custa R$ 8,00 por unidade;
b) cerâmica em forma de triângulo retângulo isósceles de catetos com 20 cm, que custa R$ 6,00 por unidade.
A sala tem largura de 5 m e comprimento de 6 m.
O construtor deseja gastar a menor quantia possível com a compra de cerâmica. Sejam x o número de peças de cerâmica de forma quadrada e y o número de peças de cerâmica de forma triangular.
Isso significa, então, encontrar valores para x e y tais que 0,04x + 0,02y ≥ 30 e que tornem o menor possível valor de
Como x é o número de peças de cerâmica de forma quadrada e y o número de peças de cerâmica de forma triangular. E que as peças quadradas custam R$ 8,00 por unidade e as peças triangulares custam R$ 6,00 por unidade. Logo, a expressão que torna o menor possível será:
= x × 8 + y × 6
= 8x + 6y
(ENEM 2014 - 2ª Aplicação).
A tabela apresenta uma estimativa da evolução da população brasileira por faixa etária, em milhões de pessoas, para 2020, 2030 e 2045.

STEFANO, F. Mais velho e mais rico: os ganhos da maturidade.
Com base na tabela, o valor que mais se aproxima da média dos percentuais da população brasileira na faixa etária até 14 anos, nos anos de 2020, 2030 e 2045, é
Como quer a média percentual. Então:
Para o ano 2020: [tex] \frac{ano\ 2020}{total} = \frac{49}{210} = 0,2333.... [tex]
Para o ano 2030: [tex] \frac{ano\ 2030}{total} = \frac{48}{223} = 0,215256 .... [tex]
Para o ano 2045: [tex] \frac{ano\ 2045}{total} = \frac{48}{236} = 0,200089 .... [tex]
Logo, a média percentual é:
[tex] \overline{X} = \frac{0,23 + 0,21 + 0,20}{3} \cong \frac{0,64}{3} [tex]
[tex] \overline{X} \cong 0,21333... [tex]
(ENEM 2014 - 2ª Aplicação).
Um artista deseja pintar em um quadro uma figura na forma de triângulo equilátero ABC de lado 1 metro. Com o objetivo de dar um efeito diferente em sua obra, o artista traça segmentos que unem os pontos médios D, E e F dos lados BC, AC e AB, respectivamente, colorindo um dos quatro triângulos menores, como mostra a figura.

Qual é a medida da área pintada, em metros quadrados, do triângulo DEF?
Primeiro vamos encontrar a área do triângulo equilátero ABC.
[tex] Área = \frac{L \sqrt{3}}{4} = \frac{1 \sqrt{3}}{4} = \frac{ \sqrt{3}}{4} [tex]
Como a área pintada, triângulo EDF, é um quarto [tex] \frac{1}{4} [tex] da área do triângulo equilátero ABC.
Logo,
[tex] \frac{\sqrt{3}}{4} \cdot \frac{1}{4} = \frac{\sqrt{3}}{16} [tex]
(ENEM 2014 - 2ª Aplicação).
A caixa-d’água de uma casa tem a forma de um paralelepípedo reto-retângulo e possui dimensões externas (comprimento, largura e altura) de, respectivamente, 4,0 m, 3,0 m e 2,5 m. É necessária a impermeabilização de todas as faces externas dessa caixa, incluindo a tampa. O fornecedor do impermeabilizante informou ao dono da casa que seu produto é fornecido em galões, de capacidade igual a 4,0 litros. Informou, ainda, que cada litro impermeabiliza uma área de 17 700 cm² e são necessárias 3 demãos de produto para garantir um bom resultado.
Com essas informações, para obter um bom resultado no trabalho de impermeabilização, o dono da casa precisará comprar um número mínimo de galões para a execução desse serviço igual a
Primeiro vamos encontrar a superfície total da caixa-d'água:

S = 2(4 × 3) + 2(3 × 2,5) + 2(4 × 2,5)
S = 2×12 + 2×7,5 + 2×10 = 24 + 15 + 20 = 59 m²
Como cada litro impermeabiliza 17 700 cm².
1 m³ ----- 10 000 cm²
x m³ ----- 17 700 cm²
x = 1,77 m³
Agora, verificar quantos litros de tinta não necessários para impermeabiliza 17 700 cm² = 1,77 m².
1 litro ---- 1,77 m²
x litros ---- (3 x 59 m²) três de mãos
[tex] x = \frac{3 \cdot 59}{1,77} = \frac{177}{1,77} = 100 L\ de\ tinta [tex]
Por final, encontrar quantos galões de tinta são necessários:
1 galão ----- 4 litros
x ----- 100 litros
[tex] x = \frac{100}{4} = 25\ galões [tex]
(ENEM 2014 - 2ª Aplicação).
Em uma cidade, os impostos que incidem sobre o consumo de energia elétrica residencial são de 30% sobre o custo do consumo mensal. O valor total da conta a ser paga no mês é o valor cobrado pelo consumo acrescido dos impostos.
Considerando x o valor total da conta mensal de uma determinada residência e y o valor dos impostos, qual é a expressão algébrica que relaciona x e y?
Impostos = 30% = 0,3
y = valor do imposto
x = valor total da conta
[tex] Valor\ dos\ impostos = \frac{taxa\ \cdot\ valor\ do\ imposto}{custo\ do\ consumo\ mensal} [tex]
[tex] Valor\ dos\ impostos = \frac{0,3 \%\ \cdot\ x}{100 \%\ +\ 30 \%} = \frac{0,3x}{1,3} [tex]
(ENEM 2014 - 2ª Aplicação).
Um cliente fez um orçamento com uma cozinheira para comprar 10 centos de quibe e 15 centos de coxinha e o valor total foi de R$ 680,00. Ao finalizar a encomenda, decidiu aumentar as quantidades de salgados e acabou comprando 20 centos de quibe e 30 centos de coxinha.
Com isso, ele conseguiu um desconto de 10% no preço do cento do quibe e de 15% no preço do cento de coxinha, e o valor total da compra ficou em R$ 1 182,00.
De acordo com esses dados, qual foi o valor que o cliente pagou pelo cento da coxinha?
Cento do quibe = q
Cento da coxinha = c
10q + 15c = 680
q + 1,5c = 68 → q = 68 – 1,5c
Como o cliente ganhou um desconto de 10% no preço do cento do quibe e 15% no preço do cento da coxinha, temos:
20q × 0,9 + 30c × 0,85 = 1182
18q + 25,5c = 1182
Substituindo q :
18(68 – 1,5c) + 25,5c = 1182
1224 – 27c + 25,5c = 1182
–1,5c = 1182 – 1224
–1,5c = – 42
[tex] c = \frac{42}{1,5} = 28 [tex]
O cento da coxinha custa R$ 28,00 mas com o desconto de 15%, temos que:
28 × 0,85 = R$ 23,80
(ENEM 2014 - 2ª Aplicação).
Uma pessoa usa um programa de computador que descreve o desenho da onda sonora correspondente a um som escolhido. A equação da onda é dada, num sistema de coordenadas cartesianas, por [tex] y = a . sen[b(x + c)][tex], em que os parâmetros a, b, c são positivos. O programa permite ao usuário provocar mudanças no som, ao fazer alterações nos valores desses parâmetros. A pessoa deseja tornar o som mais agudo e, para isso, deve diminuir o período da onda.
O(s) único(s) parâmetro(s) que necessita(m) ser alterado(s) é(são)
Alterando o parâmetro "a", altera a amplitude da onda.
Alterando o parâmetro "b", altera o comprimento da onda.
Alterando o parâmetro "c", altera o deslocamento da onda para direita ou esquerda.
Logo, opção B.
(ENEM 2014 - 2ª Aplicação).
Os sistemas de cobrança dos serviços de táxi nas cidades A e B são distintos. Uma corrida de táxi na cidade A e B são distintos. Uma corrida de táxi na cidade A é calculada pelo valor fixo da bandeirada, que é de R$ 3,45, mais R$ 2,05 por quilômetro rodado. Na cidade B, a corrida é calculada pelo valor fixo da bandeirada, que é de R$ 3,60, mais R$ 1,90 por quilômetro rodado.
Uma pessoa utilizou o serviço de táxi nas duas cidades para percorrer a mesma distância de 6 km.
Qual o valor que mais se aproxima da diferença, em reais, entre as médias do custo por quilômetro rodado ao final das duas corridas?
Vamos equacionar os dois serviços:
S(A) = 3,15 + 2,05x
S(B) = 3,60 + 1,90x
Como ambas corridas do taxi percorreu a mesma distância de 6km. Logo,
S(A) = 3,15 + 2,05 × 6 = 3,15 + 12,3 = 15,45
S(B) = 3,60 + 1,90 × 6 = 3,60 + 11,4 = 15,00
Agora, vamos encontrar a média por quilômetro de cada serviço:
[tex] S(A): Média = \frac{15,75}{6} = 2,625 [tex]
[tex] S(B): Média = \frac{15}{6} = 2,5 [tex]
Por final, encontrar a diferença entre as médias dos dois planos:
S(A) – S(B) = 2,625 – 2,5 = 0,125
Logo, a alternativa "E", mais aproximada da diferença entre as médias do custo por quilômetro.
(ENEM 2014 - 2ª Aplicação).
A figura mostra os preços da gasolina no Brasil e nos Estados Unidos (EUA), feita a conversão para reais, considerando o preço total de venda ao consumidor (abaixo dos nomes dos países) e os valores das parcelas correspondentes à refinaria, aos tributos e à distribuição e revenda.

Note que, considerando apenas a parte correspondente à refinaria, o preço da gasolina vendida no Brasil é inferior ao preço cobrado nos Estados Unidos, mas os tributos, a distribuição e a revenda aumenta o preço final de venda nos postos brasileiros.
Suponha que fosse tomada a decisão de se diminuir o preço final de venda nos postos brasileiros, sem alterar a parcela do preço da gasolina vendida na refinaria, de modo que o preço final se igualasse ao cobrado nos postos nos postos dos postos dos Estados Unidos.
Veja, ed. 2 308, ano 40,n. 7, 13 fev. 2013 (adaptado).
O percentual mais aproximado de redução dos valores em tributos, distribuição e revenda seria
No Brasil: 2,80 = 1,37 + (1,00 + 0,43) = 1,37 + 1,43.
No EUA: 2,00 = 1,52 + (0,26 + 0,22) = 1,52 + 0,46.
Como foi informado seria tomado uma decisão de diminuir o preço final nos postos brasileiros, sem alterar a parcela do preço da gasolina vendida na refinaria, de modo que o preço final se igualasse ao cobrado nos postos nos postos dos postos dos Estados Unidos.
Portanto,
1,37 + 1,43x = 1,52 + 0,46
1,43x = 2,00 – 1,37
[tex] x = \frac{0,63}{1,43} = 0,4405 \cdot 100 = 44 \% [tex]
De modo que:
100% – 44% = 56%
(ENEM 2014 - 2ª Aplicação).
Uma revista publicará os dados, apresentados no gráfico, sobre como os tipos sanguíneos estão distribuídos entre a população brasileira. Contudo, o editor dessa revista solicitou que esse gráfico seja publicado na forma de setores, em que cada grupo esteja representado por um setor circular.

O ângulo do maior desses setores medirá, em graus,
Pelo gráfico, temos o total de entrevistados:
36 + 6 + 3 + 2 + 8 + 2 + 34 + 9 = 100
Agora, vamos encontrar o valor do maior ângulo de cada tipo sanguíneo. Como pediu que cada grupo sanguíneo esteja em um mesmo setor. Então, devemos somar os Rh positivo com o negativo.
Para o grupo A: (36 + 6 = 42)
100 ----- 360°
42 ----- x
[tex] x = \frac{42\ \cdot\ 360°}{100} = \frac{15\ 120}{100} = 151,2° [tex]
Para o grupo AB: (3 + 2 = 5)
100 ---- 360°
5 ---- x
[tex] x = \frac{5\ \cdot\ 360°}{100} = \frac{1\ 800}{100} = 18° [tex]
Para o grupo B: (8 + 2 = 10)
100 ---- 360°
10 ---- x
[tex] x = \frac{10\ \cdot\ 360°}{100} = \frac{3\ 600}{100} = 36° [tex]
Para o grupo O: (34 + 9 = 43)
100 ---- 360°
43 ---- x
[tex] x = \frac{43\ \cdot\ 360°}{100} = \frac{15\ 480}{100} = 154,8° [tex]
(ENEM 2014 - 2ª Aplicação).
A vazão de água (em m³/h) em tubulações pode ser medida pelo produto da área da seção transversal por onde passa a água (em m²) pela velocidade da água (em m/h). Uma companhia de saneamento abastece uma indústria utilizando uma tubulação cilíndrica de raio r, cuja vazão da água enche um reservatório em 4 horas. Para se adaptar às normas técnicas, a companhia deve duplicar o raio da tubulação, mantendo a velocidade da água e mesmo material.
Qual o tempo esperado para encher o mesmo reservatório, após a adaptação às novas normas?
Como o novo reservatório deve manter a velocidade de vazão da água.
Então, com a alteração do raio a área será alterada. Portanto, devemos comparar as áreas antes e depois.
Reservatório antigo:
[tex] Área_{(antigo)} = πR^{2} [tex]
Reservatório novo:
[tex] Área_{(novo)} = π(2R)^{2} = 4 πR^{2} = 4 Área_{(antigo)} [tex]
[tex] Área_{(novo)} = \frac{ Área_{(antigo)}}{4} [tex]
Agora, verificar o tempo necessário para encher esse novo reservatório:
Reservatório (antigo) ----- 4 horas
[tex] \frac{Reservatório\ (novo)}{4}[tex] ----- x horas
[tex] x = \frac{1}{4} \cdot 4 = 1\ hora[tex]
(ENEM 2014 - 2ª Aplicação).
Pesquisas indicam que o número de bactérias X é duplicado a cada quarto de hora. Um aluno resolveu fazer uma observação para verificar a veracidade dessa afirmação. Ele usou uma população inicial de 105 bactérias X e encerrou a observação ao final de uma hora.
Suponha que a observação do aluno tenha confirmado que o número de bactérias X se duplica a cada quarto de hora.
Após uma hora do início do período de observação desse aluno, o número de bactérias X foi de
Veja que a cada [tex] \frac{1}{4}[tex] de hora, ou seja, 15 minutos a quantidade de bactérias dobra. Então:
10⁵ bactérias ----- t = 0 (inicio)
2 × 10⁵ bactérias ------ t = 15 min
4 × 10⁵ bactérias ------ t = 30 min
8 × 10⁵ bactérias ------ t = 45 min
16 × 10⁵ bactérias ------ t = 60 min = 1 hora
Sendo assim, temos:
16 × 10⁵ bactérias = 2⁴ × 10⁵ bactérias
(ENEM 2014 - 2ª Aplicação).
Os salários, em reais, dos funcionários de uma empresa são distribuídos conforme o quadro:

A mediana dos valores dos salários dessa empresa é, em reais,
Para obter a mediana deve ordenar os salários em ordem crescente. Portanto, como tem 48 funcionários. Então, o salário mediano é o que ocupa a ordem 24° e 25°. Então,
ordem 24° = R$ 622,00 e ordem 25° = 1 244,00.
Agora, encontrar a média aritmética entre estes dois valores:
[tex] mediana = \frac{622\ +\ 1\ 244}{2} = \frac{1\ 866}{2} = 933 [tex]
(ENEM 2014 - 2ª Aplicação).
Um ciclista participará de uma competição e treinará alguns dias da seguinte maneira: no primeiro dia, pedalará 60 km; no segundo dia, a mesma distância do primeiro mais r km; no terceiro dia, a mesma distância do segundo mais r km; e, assim, sucessivamente, sempre pedalando a mesma distância do dia anterior mais r km.
No último dia, ele deverá percorrer 180 km, completando o treinamento com um total de 1 560 km.
A distância r que o ciclista deverá pedalar a mais a cada dia, em km, é
Dados:
razão = r km
[tex] a_{1} = 60\ km [tex]
[tex] a_{n} = 180\ km [tex]
[tex]S_{n} = 1560\ km [tex]
Primeiro vamos encontrar a ordem "n"
[tex] S_{n} = \frac{(a_{1} + a_{n})\ \cdot\ n}{2} [tex]
[tex] 1560 = \frac{(60\ +\ 180) n}{2} [tex]
[tex] 3120 =240n [tex]
[tex] n = \frac{3120}{240} = 13 [tex]
Agora, encontra a razão pedida na questão:
[tex] a_{n} = a_{1} + (n - 1) \cdot r [tex]
[tex] 180 =60 + (13 - 1) \cdot r [tex]
[tex] 180 - 60 = 12r [tex]
[tex] 120 = 12r [tex]
[tex] r = \frac{120}{12} = 10\ km [tex]
(ENEM 2014 - 2ª Aplicação).
Para fazer um pião, brinquedo muito apreciado pelas crianças, um artesão utilizará o torno mecânico para trabalhar num pedaço de madeira em formato de cilindro reto, cujas medidas do diâmetro e da altura estão ilustradas na Figura 1. A parte de cima desse pião será uma semiesfera, e a parte de baixo, um cone com altura 4 cm, conforme Figura 2. O vértice do cone deverá coincidir com o centro da base do cilindro.

O artesão deseja fazer um pião com a maior altura que esse pedaço de madeira possa proporcionar e de modo a minimizar a quantidade de madeira a ser descartada.

A quantidade de madeira descartada, em centímetros cúbicos, é
Volume da figura 2: (cone + semiesfera).
[tex] Volume_{(fig.2)} = Vol_{(cone)} + Vol_{(semiesfera)} [tex]
[tex] Volume_{(fig.2)} = \frac{1}{3}πR^{2}h + \frac{\frac{4}{3}πR^{3}}{2} [tex]
[tex] Volume_{(fig.2)} = \frac{1}{3}\cdot 3\cdot 3^{2} \cdot 4 + \frac{\frac{4}{3} \cdot 3 \cdot 3^{3}}{2} [tex]
[tex] Volume_{(fig.2)} = 36 + 54 = 90\ cm^{3} [tex]
Agora, encontrar o volume da figura 1: (cilindro).
[tex] Volume_{(fig.1)} = Volume_{(cilindro)} = π R^{2} h [tex]
[tex] Volume_{(fig.1)} = Volume_{(cilindro)} = 3 \cdot 2^{2} \cdot 7 = 189\ cm^{3} [tex]
Para encontrar a quantidade de madeira descartada, é necessário subtrair o volume do cilindro pelo do pião (cone + semiesfera). Portanto,
[tex] Material\ descartado = Volume_{(cilindro)} - [Volume_{(cone)} + Volume_{(semiesfera)}] [tex]
[tex] Material\ descartado = 189 - 90 = 99\ cm^{3} [tex]
(ENEM 2014 - 2ª Aplicação).
Para as pessoas que não gostam de correr grandes riscos no mercado financeiro, a aplicação em caderneta de poupança é indicada, pois, conforme a tabela (período 2005 até 2011), a rentabilidade apresentou pequena variação.

Com base nos dados da tabela, a mediana dos percentuais de rentabilidade, no período observado, é igual a
(ENEM 2014 - 2ª Aplicação).
Uma pessoa comprou um aquário em forma de um paralelepípedo retângulo reto, com 40 cm de comprimento, 15 cm de largura e 20 cm de altura.
Chegando em casa, colocou no aquário uma quantidade de água igual à metade de sua capacidade. A seguir, para enfeitá-lo, irá colocar pedrinhas coloridas, de volume igual a 50 cm³ cada, que ficarão totalmente submersas no aquário.
Após a colocação das pedrinhas, o nível da água deverá focar a 6 cm do topo do aquário.
O número de pedrinhas a serem colocadas deve ser igual a

Como o volume do aquário já estava na metade e ao colocar as pedras o volume de água ficou a 6 cm do topo. Portanto, as pedras fez o volume da água subir 4 cm na altura.
Então, o volume das pedras corresponde ao volume do paralelepípedo de dimensões: (40 cm × 15 cm × 4cm). Logo,
V = 40 cm × 15 cm × 4 cm
V = 2 400 cm³.
Como cada pedra possui 50 cm³. Então, a quantidade de pedrinhas colocadas no aquário é:
[tex] Quant.\ de\ pedras = \frac{2400}{50} = 48\ pedras [tex]
(ENEM 2014 - 2ª Aplicação).
Em 2010, cerca de 3,24 milhões de passageiros foram transportados entre os Estados Unidos e o Brasil, de acordo com dados divulgados pela Agência Nacional de Aviação Civil (Anac). O gráfico mostra a distribuição relativa do número de passageiros transportados entre o Brasil e os cinco destinos mais procurados, dos quais apenas dois países são europeus: França e Portugal.

De acordo com esses dados, o valor mais aproximado para a quantidade total de passageiros transportados em 2010 entre o Brasil e os países europeus mostrados no gráfico é
Pelo gráfico, os países europeus (Portugal e França) soma 27% (11% + 16%) de passageiros transportados. Então, a quantidade total de passageiros transportados em 2010 entre o Brasil e os países europeus é:
3,24 milhões ----- 35%
x milhões ----- 27%
[tex] x = \frac{3,24\ \cdot\ 27}{35} = \frac{87,48}{35} = 2\ 499,42\ milhões [tex]
Ou seja,
2,499428 milhões = 2 499 428
(ENEM 2014 - 2ª Aplicação).
O Brasil desenvolveu técnicas próprias de plantio e colheita de cana-de-açúcar, tornando-se o maior produtor mundial. Cultivando novas variedades, foram produzidas, na safra 2010/2011, 624 milhões de toneladas em 8,1 milhões de hectares. Houve um substancial ganho de produtividade (em toneladas por hectare) quando se compara com a de décadas atrás, como a da safra 1974/1975, que foi de 47 toneladas por hectare.
Disponível em: www2.cead.ufv.br. Acesso em: 27 fev. 2011 (adaptado).
De acordo com dados apresentados, qual foi o valor mais aproximado da taxa de crescimento da produtividade de cana-de-açúcar, por hectare no Brasil, da safra 1974/1975 para a safra 2010/2011?
Primeiro vamos encontrar a quantidade de toneladas por hectares na safra 2010/2011.
[tex] \frac{624\ milhões}{8,1\ milhões} = 77,03\ ton/hec [tex]
Agora, encontrar a taxa de crescimento:
47 ton/hec ------ 100%
77,03 ton/hec ------ x %
[tex] \frac{77,03\ \cdot\ 100}{47} = 163,89 \% [tex]
Logo,
[tex] 163,89 \%\ –\ 100 \% = 63,89 \% \cong 64 \% [tex]
(ENEM 2014 - 2ª Aplicação).
O número de frutos de uma determinada espécie de planta se distribui de acordo com as probabilidades apresentadas no quadro.
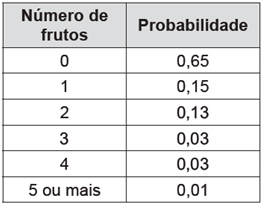
A probabilidade de que, em tal planta, existam, pelo menos, dois frutos é igual a
Pelo gráfico constatamos que:

0,13 + 0,03 + 0,06 + 0,01 = 0,20 × 100 = 20%
(ENEM 2014 - 2ª Aplicação).
Um procedimento padrão para aumentar a capacidade do número de senhas de banco é acrescentar mais caracteres a essa senha. Essa prática, além de aumentar as possibilidades de senha, gera um aumento na segurança. Deseja-se colocar dois novos caracteres na senha de um banco, um no início e outro no final. Decidiu-se que esses novos caracteres devem ser vogais e o sistema conseguirá diferenciar maiúsculas de minúsculas.
Com essa prática, o número de senhas possíveis ficará multiplicado por
De acordo com as informações no texto, temos:
vogais: a, e, i, o, u = 5
maiúsculas e minúsculas = 2
Logo,

Portanto, há 10 x 10 = 100 possibilidades distintas.
(ENEM 2014 - 2ª Aplicação).
André, Carlos e Fábio estudam em uma mesma escola e desejam saber quem mora mais perto da escola.
André mora a cinco vinte avos de um quilômetro da escola. Carlos mora a seis quartos de um quilômetro da escola. Já Fábio mora a quatro sextos de um quilômetro da escola.
A ordenação dos estudantes de acordo com a ordem decrescente das distâncias de suas respectivas casas à escola é
Distância de André:
[tex] \frac{5}{20}km = \frac{5}{20}\cdot 1000m = \frac{5000}{20} = 250\ m [tex]
Distância de Carlos:
[tex] \frac{6}{4}km = \frac{6}{4}\cdot 1000m = \frac{6000}{4} = 1500\ m [tex]
Distância de Fábio:
[tex] \frac{4}{6}km = \frac{4}{6}\cdot 1000m = \frac{4000}{6} = 666,66\ m [tex]
Logo,
[tex] D_{(Carlos)} > D_{(Fábio)} > D_{(André)} [tex]
(ENEM 2014 - 2ª Aplicação).
Alunos de um curso de engenharia desenvolveram um robô “anfíbio” que executa saltos somente nas direções norte, sul, leste e oeste. Um dos alunos representou a posição inicial desse robô, no plano cartesiano, pela letra P, na ilustração.

A direção norte-sul é a mesma do eixo y, sendo que o sentido norte é o sentido de crescimento de y, e a direção leste-oeste é a mesma do eixo x, sendo que o sentido leste é o sentido de crescimento de x.
Em seguida, esse aluno deu os seguintes comandos de movimentação para o robô: 4 norte, 2 leste e 3 sul, nos quais os coeficientes numéricos representam o número de saltos do robô nas direções correspondentes, e cada salto corresponde a uma unidade do plano cartesiano.
Depois de realizar os comandos dados pelo aluno, a posição do robô, no plano cartesiano, será

Logo, a posição do robô é (1; 2).
(ENEM 2014 - 2ª Aplicação).
Um clube de futebol abriu inscrições para novos jogadores. Inscreveram-se 48 candidatos. Para realizar uma boa seleção, deverão ser escolhidos os que cumpram algumas exigências: os jogadores deverão ter mais de 14 anos, estatura igual ou superior à mínima exigida e bom preparo físico. Entre os candidatos, [tex]\frac{7}{8}[tex] têm mais de 14 anos e foram pré-selecionados. Dos pré-selecionados, [tex]\frac{1}{2}[tex] têm estatura igual ou superior à mínima exigida e, destes, [tex]\frac{2}{3}[tex] têm bom preparo físico.
A quantidade de candidatos selecionados pelo clube de futebol foi
Ter mais de 14 anos:
[tex] \frac{7}{8} \cdot 48 = \frac{336}{8} = 42\ candidatos [tex]
Ter estatura igual ou superior à mínima exigida:
[tex] \frac{1}{2} \cdot 42 = \frac{42}{2} = 21\ candidatos [tex]
Ter bom preparo físico:
[tex] \frac{2}{3} \cdot 21 = \frac{42}{3} = 14\ candidatos [tex]
(ENEM 2014 - 2ª Aplicação).
Barras de cobre cilíndricas são utilizadas para fazer aterramentos elétricos.
Durante a instalação de um chuveiro, uma pessoa utilizou uma barra de aterramento de densidade ρ, massa m, diâmetro D = 2R e altura h.
Para fazer um novo aterramento, essa pessoa utilizou uma barra com a mesma densidade, mas com o dobro da massa e dobro do diâmetro em relação à usada no chuveiro. A densidade é dada por [tex] p = \frac{m}{v} [tex] e o volume da barra cilíndrica é [tex] V = πR^{2}h[tex].
Qual a relação da altura da barra utilizada no novo aterramento comparada àquela utilizada no aterramento do chuveiro?
Dados:
Densidade: [tex] p = \frac{m}{v} [tex]
Volume: [tex] V = πR^{2}h [tex]
Barras com mesma densidades
Antes:
[tex] p_{1} = \frac{m}{V_{1}} → V_{1} = \frac{m}{p_{1}} [tex]
e
[tex] V_{1} = πR^{2}h_{1} → \frac{m}{p_{1}} = πR^{2}h_{1} → p_{1} = \frac{ πR^{2}h_{1}}{m} [tex]
Depois:
[tex] p_{2} = \frac{2m}{V_{2}} → V_{2} = \frac{2m}{p_{2}} [tex]
e
[tex] V_{2} = π(2R)^{2}h_{2} → \frac{2m}{p_{2}} = 4πR^{2}h_{2} → p_{2} = \frac{ 2πR^{2}h_{2}}{m} [tex]
Como as barras tem a mesma densidade. Logo,
[tex] p_{1} = p_{2} [tex]
[tex] \frac{πR^{2}h_{1}}{m} = \frac{2πR^{2}h_{2}}{m} [tex]
[tex] h_{2} = \frac{h_{1}}{2} [tex]
Portanto, a altura será a metade da barra utilizada no novo aterramento comparada àquela utilizada no aterramento do chuveiro.
(ENEM 2014 - 2ª Aplicação).
O Brasil é o quarto produtor mundial de alimentos, mas aproximadamente 64 toneladas de cada 100 toneladas que se produz são perdidas ao longo da cadeia produtiva.
Em relação ao total de alimentos produzidos, a perda de alimentos é distribuída da seguinte forma: 20 toneladas na colheita, 8 toneladas no transporte e armazenamento, 15 toneladas na indústria de processamento, 1 tonelada no varejo e 20 toneladas no processamento culinário e hábitos alimentares.
Disponível em: www.bancodealimentos.org.br. Acesso em: 26 out. 2011 (adaptado).
De acordo com os dados apresentados, os alimentos que são perdidos no processamento culinário e nos hábitos alimentares representam qual porcentagem em relação ao total de alimentos que são perdidos no país?
Como foi informado no texto, 20 toneladas, foi a quantidade de alimentos perdidos no processamento culinário e hábitos alimentares. Logo,
[tex] \frac{20\ ton}{64\ ton} = 0,3125 \cdot 100 = 32,25 \% [tex]
(ENEM 2014 - 2ª Aplicação).
Um confeiteiro deseja fazer um bolo cuja receita indica a utilização de açúcar e farinha de trigo em quantidades fornecidas em gramas. Ele sabe que uma determinada xícara utilizada para medir os ingredientes comporta 120 gramas de farinha de trigo e que três dessas xícaras de açúcar correspondem, em gramas, a quatro de farinha de trigo.
Quantos gramas de açúcar cabem em uma dessas xícaras?
Veja que:
3 xíc. de açúcar ----- 4 xíc. de farinha
1 xíc. de açúcar ----- x
[tex] x = \frac{4}{3} [tex]
Portanto,
[tex] x = \frac{4}{3} \cdot 120\ g = 160\ gramas [tex]
(ENEM 2014 - 2ª Aplicação).
Uma fundição de alumínio utiliza, como matéria-prima, lingotes de alumínio para a fabricação de peças injetadas. Os lingotes são derretidos em um forno e o alumínio, em estado líquido, é injetado em moldes para se solidificar no formato desejado. O gráfico indica as curvas de resfriamento do alumínio fundido no molde para três diferentes fluidos refrigerantes (tipo I, tipo II e tipo III), que são utilizados para resfriar o molde, bem como a curva de resfriamento quando não é utilizado nenhum tipo de fluido refrigerante. A peça só pode ser retirada do molde (desmolde) quando atinge a temperatura de 100 °C.
Para atender a uma encomenda, a fundição não poderá gastar mais do que 8 segundos para o desmolde da peça após a sua injeção.

Com a exigência para o desmolde das peças injetadas, qual(is) fluido(s) refrigerante(s) poderá(ão) ser utilizado(s) no resfriamento?
Pelas informações do texto e do gráficos, obtemos:

(ENEM 2014 - 2ª Aplicação).
O modelo matemático desenvolvido por Kirschner e Webb descreve a dinâmica da interação das células não infectadas do sistema imunológico humano com os vírus HIV. Os grupos mostram a evolução no tempo da quantidade de células não infectadas no sistema imunológico de cinco diferentes pacientes infectados pelos vírus HIV. Quando a população das células não infectadas de um sistema imunológico é extinta, o paciente infectado fica mais suscetível à morte, caso contraia alguma outra doença.

KIRSCHNER, D. E.: WEBB.G. F. Resistance, Remission, and Qualitative Differences is HIV Chemotherapy. Emerging Infectious Diseases v. 3, n. 3, 1997.
A partir desses dados, o sistema imunológico do paciente infectado que ficou mais rapidamente suscetível à morte está representado pelo gráfico.
Simplesmente interpretação do texto e do gráfico. Portanto, o gráfico que apresenta o sistema imunológico mais baixo em função do tempo é o gráfico D.


Nenhum comentário:
Postar um comentário