(ENEM 2020 - 2ª Aplicação).
Um curso é oferecido aos fins de semana em três cidades de um mesmo estado. Alunos matriculados nesse curso são moradores de cidades diferentes. Eles se deslocam para uma das três cidades onde o curso é oferecido ao sábado pela manhã, pernoitam nessa cidade para participar das atividades no domingo e retornam às suas casas no domingo à noite. As despesas com alimentação e hospedagem são custeadas pela coordenação do curso. A tabela mostra essas despesas, por fim de semana, registradas no ano passado.
| Cidade | Alimentação (R$) | Hospedagem (R$) |
|---|---|---|
| A | 1 400 | 1 800 |
| B | 800 | 2 000 |
| C | 1 500 | 3 500 |
Para planejar as despesas para o próximo ano, a coordenação precisa levar em conta um aumento de:
• 15% com hospedagem na cidade A;
• 20% com alimentação na cidade B;
• 5% com alimentação na cidade C.
O aumento no orçamento das despesas com alimentação e hospedagem por fim de semana do curso para este ano, em porcentagem, em relação às do ano anterior, é melhor aproximado por
Primeiro calcular o valor (V) total das despesas com hospedagem.
[tex]V = 1400 + 1800 + 800 + 2000+ 1500 + 3500[tex]
[tex]V = 11\ 000,00[tex]
Agora, o aumento das despesas (D):
[tex]D = 1800 \cdot 1,5 + 800 \cdot 0,2 + 1500 \cdot 0,05 [tex]
[tex]D = 270 + 160 + 75[tex]
[tex]D = 505,00[tex]
Por último calcular as despesas em porcentagem.
[tex]11\ 000 ----\ 100 \%\ [tex]
[tex]505 ----\ x \%\ [tex]
[tex] 11\ 000x = 505 \cdot 100 [tex]
[tex] x = \frac{50\ 500}{11\ 000} [tex]
[tex] x \cong 4,59 \%\ [tex]
Portanto, alternativa "A".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Pretende-se comprar uma mesa capaz de acomodar 6 pessoas, de modo que, assentadas em torno da mesa, cada pessoa disponha de, pelo menos, 60 cm de espaço livre na borda do tampo da mesa, que deverá ter a menor área possível. Na loja visitada há mesas com tampos nas formas e dimensões especificadas:
• Mesa I: hexágono regular, com lados medindo 60 cm;
• Mesa II: retângulo, com lados medindo 130 cm e 60 cm;
• Mesa III: retângulo, com lados medindo 120 cm e 60 cm;
• Mesa IV: quadrado, com lados medindo 60 cm;
• Mesa V: triângulo equilátero, com lados medindo 120 cm.
A mesa que atende aos critérios especificados é a
Primeiro analisar a condição de caber 6 pessoas, sendo que cada deve ter no mínimo 60 cm na borda da mesa. Portanto, a mesa deve ter um perímetro de mínimo 360 cm.
• Mesa I: 6 × 60 = 360 cm;
• Mesa II: 2 × 130 + 2 × 60 = 260 + 120 = 380 cm;
• Mesa III: 2 × 120 + 2 × 60 = 240 + 120 = 360 cm;
• Mesa IV: 4 × 60 = 240 cm; (Não satisfaz!)
• Mesa V: 3 × 120 = 360 cm;
Agora, verificar a mesa de menor área.
• Mesa I: [tex] A = \frac{L^{2} \cdot 2\sqrt{3}}{2} = \frac{60^{2} \cdot 2\sqrt{3}}{2} [tex]
[tex] = \frac{3600 \cdot 2\sqrt{3}}{2} = 5400\sqrt{3}\ cm^{2} [tex]
• Mesa II: [tex] A = b \cdot h = 130 \cdot 60 = 7\ 800\ cm^{2} [tex]
• Mesa III: [tex] A = b \cdot h = 120 \cdot 60 = 7\ 200\ cm^{2} [tex]
• Mesa V: [tex] A = \frac{a^{2} \cdot \sqrt{3}}{4} = \frac{120^{2} \cdot \sqrt{3}}{4} = \frac{14\ 400 \cdot \sqrt{3}}{4} [tex]
[tex] = 3600 \cdot \sqrt{3} \cong 3600 \cdot 1,7 \cong 6\ 120\ cm^{2} [tex]
Sendo assim, a mesa que satisfaz a situação descrita acima é a mesa V.
Portanto, alternativa "E".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Uma partida de futebol tem dois tempos de 45 minutos cada. A duração do intervalo entre cada tempo é de 15 minutos. Eventualmente, por ocasião de paralisações ocorridas durante um dos tempos (como comemorações de gols, atendimento a jogadores que necessitem de maca), ocorre acréscimo ao tempo de jogo.
No Brasil, o segundo tempo é iniciado zerando-se o cronômetro, mas em campeonatos europeus, começa com o cronômetro posicionado em 45 minutos. Em uma partida de um campeonato europeu, um time marcou um gol aos 17 minutos e 45 segundos. A outra equipe empatou o jogo aos 54 minutos e 32 segundos. O tempo do intervalo foi respeitado e houve um acréscimo de 2 minutos ao primeiro tempo do jogo.
O tempo transcorrido entre os dois gols foi de
Calculo do intervalo de tempo:
[tex]∆t = t_{F}\ –\ t_{i} [tex]
[tex] ∆t = 54min32s\ –\ 17min45s [tex]
[tex] ∆t = 53min92s\ –\ 17min45s [tex]
[tex] ∆t = 36min47s [tex]
Agora, devemos acrescentar o tempo do intervalo (15 min) e um acréscimo de 2 minutos.
[tex]t = 36min47s + 15min + 2min [tex]
[tex]t = 53min47s [tex]
Portanto, alternativa "B".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Um laboratório realizou um teste para calcular a velocidade de reprodução de um tipo de bactéria. Para tanto, realizou um experimento para observar a reprodução de uma quantidade x dessas bactérias por um período de duas horas. Após esse período, constava no habitáculo do experimento uma população de 189 440 da citada bactéria. Constatou-se, assim, que a população de bactérias dobrava a cada 0,25 hora.
A quantidade inicial de bactérias era de
Dados:
Total de bactérias: [tex]B = 189\ 440[tex]
[tex]B_{0}[tex] = total inicial de bactérias = ?
Razão: 2
Tempo: [tex]t = 2h =[tex] 8[tex] × 0,25 h[tex]
Logo, a função exponencial ficará:
[tex] B(t) = B_{0} \cdot 2^{t}[tex]
[tex] 189\ 440 = B_{0} \cdot 2^{8}[tex]
[tex] 189\ 440 = B_{0} \cdot 256[tex]
[tex] \frac{189\ 440}{256} = B_{0}[tex]
[tex]B_{0} = 740\ bactérias[tex]
Portanto, alternativa "B".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
O valor cobrado por uma corrida de táxi é calculado somando-se a bandeirada, um valor fixo que é cobrado em qualquer corrida, a um valor variável que depende da distância percorrida.
Uma empresa de táxi cobra pela bandeirada o valor de R$ 4,50. Para corridas de até 200 metros, é cobrada somente a bandeirada, e para corridas superiores a 200 metros é cobrado o valor de R$ 0,02 para cada metro adicional percorrido.
Para analisar o valor cobrado, em real, em função da distância percorrida, em metro, a empresa elaborou um gráfico, com uma simulação para uma distância de 600 metros.
O gráfico que representa o valor da corrida, em real, em função da distância percorrida, em metro, é
Para os primeiros 200 metros paga-se a bandeirada, um valor fixo de R$ 4,50.
Agora, verificar o valor pago para uma corrida de 600 m.
[tex] P(x) = P_{(fixa)} + P_{(variável)} [tex]
[tex] P(x) = 4,50 + 0,02 \cdot x [tex]
[tex] P(600) = 4,50 + 0,02 \cdot (600\ -\ 200) [tex]
[tex] P(600) = 4,50 + 0,02 \cdot 400 [tex]
[tex] P(600) = 4,50 + 8,00 [tex]
[tex] P(600) = R \$\ 12,50 [tex]
Sendo assim, o gráfico “D” satisfaz a situação descrita.
Portanto, alternativa "D".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Uma dona de casa vai ao supermercado para comprar dois fardos de refrigerantes, contendo cada um deles seis unidades de 0,6 litro. Lá chegando, verificou não existirem fardos nem no formato e nem na capacidade desejados. Decidiu, então, comprar os refrigerantes em unidades avulsas, de mesma capacidade, de forma a obter, no mínimo, a mesma quantidade de líquido desejada inicialmente, gastando o mínimo de dinheiro. As opções de embalagens e respectivos preços existentes no supermercado são dados no quadro.
| Embalagem (L) | Custo (R$) |
|---|---|
| 3 | 4,39 |
| 2,5 | 3,69 |
| 2 | 2,89 |
| 1,5 | 2,19 |
| 1 | 1,99 |
Qual é a opção de embalagem, em litro, que proporcionará maior economia para essa dona de casa?
O total de refrigerantes, em litros é:
[tex]= 2 × 6 × 0,6 L = 7,2 [tex] Litros
Agora, analisar cada tipo de embalagens:
• De 3L: [tex] 3 × 4,39 = R \$\ 13,17 [tex]
• De 2,5L: [tex] 3 × 3,69 = R \$\ 11,07 [tex]
• De 2L: [tex] 4 × 2,89 = R \$\ 11,56 [tex]
• De 1,5L: [tex] 5 × 2,19 = {\color{Red}{R \$\ 10,95}} [tex]
• De 1L: [tex] 8 × 1,99 = R \$\ 15,92 [tex]
Sendo assim, comprar a embalagem de 1,5L proporcionará maior economia para a dona de casa.
Portanto, alternativa "B".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Após o término das inscrições de um concurso, cujo número de vagas é fixo, foi divulgado que a razão entre o número de candidatos e o número de vagas, nesta ordem, era igual a 300. Entretanto, as inscrições foram prorrogadas, inscrevendo-se mais 4 000 candidatos, fazendo com que a razão anteriormente referida passasse a ser igual a 400. Todos os candidatos inscritos fizeram a prova, e o total de candidatos aprovados foi igual à quantidade de vagas. Os demais candidatos foram reprovados.
Nessas condições, quantos foram os candidatos reprovados?
Equacionando o problema.
[tex]c = candidato[tex]
[tex]v = vaga[tex]
[tex] \begin{cases} \frac{c}{v} = 300 \\ \frac{c\ +\ 4000}{v} = 400 \end{cases} \rightarrow \begin{cases} c = 300v \\ c + 4\ 000 = 400v \end{cases}[tex]
Agora, resolvendo o sistema:
[tex] c + 4\ 000 = 400v [tex]
[tex] 300v + 4\ 000 = 400v [tex]
[tex] 4\ 000 = 400v\ -\ 300v [tex]
[tex] 4\ 000 = 100v [tex]
[tex] v = \frac{4\ 000}{100} = 40\ vagas [tex]
Calculando agora, o número de candidatos.
[tex] c = 300v [tex]
[tex] c = 300 \cdot 40 [tex]
[tex] c = 12\ 000\ candidatos [tex]
Agora, encontrando o total de candidatos que fizeram a prova.
[tex] T = 12\ 000 + 4\ 000 = 16\ 000 [tex]
Como o total de candidatos aprovados é igual à quantidade de vagas e os demais candidatos foram reprovados. Então:
[tex] reprovados = 16\ 000\ -\ 40 = 15\ 960\ candidatos [tex]
Portanto, alternativa "C".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Usando um computador construído com peças avulsas, o japonês Shigeru Kondo calculou o valor da constante matemática 𝜋 com precisão de 5 trilhões de dígitos. Com isso, foi quebrado o recorde anterior, de dois trilhões de dígitos, estabelecido pelo francês Fabrice Bellard.
Disponível em: www.estadao.com.br. Acesso em: 14 dez. 2012.
A quantidade de zeros que segue o algarismo 5 na representação do número de dígitos de 𝜋 calculado pelo japonês é
Como o valor da constante matemática 𝜋 com precisão de 5 trilhões de dígitos. Então:
[tex] 5\ trilhões = 5\ \underbrace{\color{Red}{000\ 000\ 000\ 000}}_{12\ zeros} [tex]
Sendo assim, o número é composto por 12 zeros após o algarismo 5.
Portanto, alternativa "D".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
O gerente de uma concessionária apresentou a seguinte tabela em uma reunião de dirigentes. Sabe-se que ao final da reunião, a fim de elaborar metas e planos para o próximo ano, o administrador avaliará as vendas, com base na mediana do número de automóveis vendidos no período de janeiro a dezembro.
| Mês | Número de automóveis vendidos |
|---|---|
| Janeiro | 25 |
| Fevereiro | 20 |
| Março | 30 |
| Abril | 35 |
| Maio | 40 |
| Junho | 50 |
| Julho | 45 |
| Agosto | 35 |
| Setembro | 60 |
| Outubro | 55 |
| Novembro | 70 |
| Dezembro | 65 |
Qual foi a mediana dos dados apresentados?
Primeiro colocar em ordem crescente o número de automóveis vendidos:
[tex] 20, 25, 30, 35, 35, \color{Red}{40, 45}, 50, 55, 60, 65, 70[tex]
Agora, calcular a média aritmética entre 40 e 45.
[tex] Mediana = \frac{40\ +\ 45}{2} = \frac{85}{2} = 42,5 [tex]
Portanto, alternativa "B".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
No desenho técnico, é comum representar um sólido por meio de três vistas (frontal, perfil e superior), resultado da projeção do sólido em três planos, perpendiculares dois a dois.
A figura representa as vistas de uma torre.

Disponível em: www.uems.br. Acesso em: 11 dez. 2012 (adaptado).
Com base nas vistas fornecidas, qual figura melhor representa essa torre?

Analisando as vistas, percebemos que a figura “E”, contempla as vistas da torre.
Portanto, alternativa "E".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
O governador de um estado propõe a ampliação de investimentos em segurança no transporte realizado por meio de trens. Um estudo para um projeto de lei prevê que se tenha a presença de três agentes mulheres, distribuídas entre os 6 vagões de uma composição, de forma que duas dessas agentes não estejam em vagões adjacentes, garantindo assim maior segurança aos usuários.
Disponível em: www.sisgraph.com.br. Acesso em: 29 jan. 2015 (adaptado).
A expressão que representa a quantidade de maneiras distintas das três agentes serem distribuídas nos vagões é
De acordo com o enunciado: "duas dessas agentes não estejam em vagões adjacentes".
Podemos ter a seguinte disposição, sendo A, o vagão com agente e V, vagão sem agente.
Logo, são 4 configurações possíveis. Ou seja, [tex] C_{4}^{3}[tex].
Agora, para finalizar, temos que analisar a ordem das agentes dentro de um mesmo vagão. Como são 3 agentes e que a ordem delas importa. Portanto, é arranjo. Como são 3 agentes e 3 vagões pode visto como permutação simples. Ou seja, [tex]P_{3} = 3![tex].
Sendo assim:
[tex] C_{4}^{3} × 3! [tex]
Portanto, alternativa "C".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Em uma campanha promocional de uma loja, um cliente gira uma roleta, conforme a apresentada no esquema, almejando obter um desconto sobre o valor total de sua compra. O resultado é o que está marcado na região apontada pela seta, sendo que todas as regiões são congruentes. Além disso, um dispositivo impede que a seta venha a apontar exatamente para a linha de fronteira entre duas regiões adjacentes. Um cliente realiza uma compra e gira a roleta, torcendo para obter o desconto máximo.

A probabilidade, em porcentagem, de esse cliente ganhar o desconto máximo com um único giro da roleta é melhor aproximada por
A probabilidade do desconto máximo com um único giro da roleta é:
[tex] P = \frac{Evento}{Espaço\ amostral} [tex]
[tex] P = \frac{1}{12} = 0,83333... \cong 8,33 \%\ [tex]
Portanto, alternativa "A".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Um dos conceitos mais utilizados nos estudos sobre a dinâmica de populações é o de densidade demográfica. Esta grandeza, para um local, é a razão entre o seu número de habitantes e a medida da área do seu território. Quanto maior essa razão, expressa em habitante por quilometro quadrado, se diz que mais densamente povoado é o local.
Querendo fazer uma visita de estudos ao local mais densamente povoado, entre um grupo de cinco escolhidos, um geógrafo coletou as informações sobre população e área territorial dos locais de seu interesse, obtendo os dados apresentados no quadro, referentes ao ano de 2014.
| População (N° habitantes) | Área (km²) | |
|---|---|---|
| Malta | 400 000 | 300 |
| Brasil | 200 000 000 | 9 000 000 |
| México | 120 000 000 | 2 000 000 |
| Namíbia | 2 000 000 | 820 000 |
| Ilha Norfolk | 1 841 | 35 |
Disponível em: www.indexmundi.com. Acesso em: 13 nov. 2015 (adaptado).
Para cumprir seu objetivo de visita, qual dos locais apresentados deverá ser o escolhido pelo geógrafo?
Calcular a densidade demográfica de cada país.
| Densidade (hab/km²) | |
|---|---|
| Malta | [tex]\frac{400\ 000}{300} \cong 1\ 333,33 [tex] |
| Brasil | [tex]\frac{200\ 000\ 000}{9\ 000\ 000} \cong 22,22 [tex] |
| México | [tex]\frac{120\ 000\ 000}{2\ 000\ 000} \cong 60 [tex] |
| Namíbia | [tex]\frac{2\ 000\ 000}{820\ 000} \cong 2,44[tex] |
| Ilha Norfolk | [tex]\frac{1\ 841}{35} \cong 52,6 [tex] |
Portanto, alternativa "A".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Para identificar visualmente uma loja de pet shop, um empresário criou uma logomarca que se assemelha a uma marca deixada pela pegada de um gato, como na figura. O maior círculo tem medida de raio igual a 6 cm. O empresário pretende reproduzir o desenho em uma das paredes retangulares da loja. Para isso, fará a ampliação da logomarca utilizando a escala de 1 : 25.

A área mínima, em metro quadrado, que a parede deverá ter para que a logomarca seja aplicada é A
(ENEM 2020 - 2ª Aplicação).
Os pesquisadores de uma empresa especializada em grãos selecionaram cinco diferentes tipos de semente de feijão e concluíram que, quando armazenadas por até seis meses, o poder germinativo de cada um desses tipos expressa, em porcentagem, quantas sementes são capazes de germinar, transcorrido o tempo de armazenamento correspondente. Considere que o tempo zero corresponde ao plantio direto da semente sem armazenamento, conforme descrito no quadro.
| Semente de feijão | Tempo de armazenamento (em mês) | ||
|---|---|---|---|
| 0 | 3 | 6 | |
| Poder germinativo (em %) | |||
| Tipo 1 | 84 | 84 | 79 |
| Tipo 2 | 85 | 82 | 79 |
| Tipo 3 | 86 | 80 | 77 |
| Tipo 4 | 82 | 82 | 80 |
| Tipo 5 | 85 | 85 | 76 |
Um agricultor irá plantar três áreas distintas utilizando sementes de um mesmo tipo. A primeira área será plantada quando da aquisição das sementes, a segunda, três meses após a primeira e a terceira, três meses após a segunda, respeitando assim o tempo de armazenamento utilizado pelos pesquisadores. Esse agricultor irá optar pela compra do tipo de semente que apresentar a maior média dos três percentuais de poder germinativo.
Disponível em: http://sistemasdeproducao .cnptia.embrapa.br. Acesso em: 22 out. 2015 (adaptado).
Segundo essas informações, qual será o tipo de semente a ser adquirida por ele?
Calculando a média aritmética dos tipos de feijão.
| Tipo de feijão | Média aritmética |
|---|---|
| Tipo 1 | [tex]\frac{84\ +\ 84\ +\ 79}{3} = \frac{247}{3} \cong 83,33 [tex] |
| Tipo 2 | [tex]\frac{85\ +\ 82\ +\ 79}{3} = \frac{246}{3} = 82 [tex] |
| Tipo 3 | [tex]\frac{86\ +\ 80\ +\ 77}{3} = \frac{243}{3} = 81 [tex] |
| Tipo 4 | [tex]\frac{82\ +\ 82\ +\ 80}{3} = \frac{244}{3} \cong 81,33 [tex] |
| Tipo 5 | [tex]\frac{85\ +\ 85\ +\ 76}{3} = \frac{246}{3} = 82 [tex] |
O agricultor deverá escolher o tipo 1 de feijão por apresentar maior média percentual.
Portanto, alternativa "A".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
O quadro mostra o número de gols feitos pela equipe A em campeonatos estaduais de futebol, no período de 2007 a 2012.
| Ano | Número de gols |
|---|---|
| 2007 | 64 |
| 2008 | 59 |
| 2009 | 61 |
| 2010 | 45 |
| 2011 | 61 |
| 2012 | 58 |
Faltando ainda alguns jogos para o término do campeonato estadual de 2013, o número de gols marcados pela equipe B era 52. O técnico dessa equipe fez um levantamento para saber quantos gols sua equipe deveria marcar nos próximos jogos de modo que, ao final do campeonato, o número total de gols marcados pela equipe B ultrapasse a média de gols marcados pela equipe A nos campeonatos de 2007 a 2012.
Quantos gols, no mínimo, a equipe B ainda precisaria marcar?
Calculando a média de gols da equipe “A”.
[tex] M_{(A)} = \frac{64 + 59 + 61 + 45 + 61 + 58}{6} = \frac{348}{6} = 58[tex]
Agora, encontrar a quantidade mínima de gols que a equipe “B” precisa fazer para ultrapassar a equipe A. Como a equipe B já fez 52 gols. Logo:
[tex] 58 - 52 = 6\ gols [tex]
Portanto, a equipe B deve fazer no mínimo 7 gols para ultrapassar a equipe A.
Portanto, alternativa "C".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Provedores de conteúdos postam anúncios de empresas em seus websites. O provedor A cobra R$ 0,10 por clique feito no anúncio, além do pagamento de uma taxa de contratação de R$ 50,00. O provedor B cobra uma taxa de contratação por anúncio mais atrativa, no valor de R$ 20,00, mais um valor por clique feito no anúncio. Para um anúncio que receberá 100 cliques, o provedor B fixará uma proposta com um valor a ser cobrado por clique, de modo que venha a receber, pelo menos, o mesmo total que receberia o provedor A.
O gerente do provedor B deve avaliar os valores por clique a serem fixados.
O valor mínimo que o gerente do provedor B deverá escolher é
Equacionando o problema, para um total de 100 cliques:
[tex] Provedor\ A = Provedor\ B [tex]
[tex] 0,10 \cdot 100 + 50 = 20 + 100 \cdot x [tex]
[tex] 10 + 50 = 20 + 100x [tex]
[tex] 60 - 20 = 100x [tex]
[tex] \frac{40}{100} = x [tex]
[tex] x = R \$\ 0,40 [tex]
Portanto, alternativa "D".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
O índice pluviométrico é uma medida, em milímetro, que fornece a quantidade de precipitação de chuva num determinado local e num intervalo de tempo (hora, dia, mês e/ou ano). Os valores mensais do índice pluviométrico de uma cidade brasileira, no primeiro semestre, são mostrados no gráfico.
De acordo com a previsão meteorológica, o índice pluviométrico no mês de julho será igual ao índice do mês de junho somado à variação correspondente ao maior acréscimo, em milímetro, do índice pluviométrico entre dois meses consecutivos do semestre apresentado.
O índice pluviométrico, em milímetro, previsto para o mês de julho, na cidade considerada, será igual a
Como o mês de julho será igual ao índice do mês de junho somado à variação correspondente ao maior acréscimo, em milímetro.
Encontrando a variação entre dois meses consecutivos que ocorreu acréscimo:
• Mar e Abr: [tex]|30\ – 70| = 40\ mm[tex]
• Abr e Mai: [tex]|70\ – 90| = 20\ mm[tex]
Sendo assim, o índice pluviométrico, em milímetro, previsto para o mês de julho, na cidade considerada, será igual a:
[tex]= mês\ de\ junho + maior\ variação\ de\ acréscimo [tex]
[tex]= 10 + 40 [tex]
[tex]= 50\ mm[tex]
Portanto, alternativa "B".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Um banho propicia ao indivíduo um momento de conforto e reenergização. Porém, o desperdício de água gera prejuízo para todos. Considere que cada uma das cinco pessoas de uma família toma dois banhos por dia, de 15 minutos cada. Sabe-se que a cada hora de banho são gastos aproximadamente 540 litros de água. Considerando que um mês tem 30 dias, podemos perceber que o consumo de água é bem significativo.
A quantidade total de litros de água consumida, nos banhos dessa família, durante um mês, é mais próxima de
A quantidade total de litros de água consumida, nos banhos dessa família, é de:
[tex] Q = 5\ pessoas \cdot 2\ banhos \cdot 15min \cdot 540 L/h \cdot 30 dias [tex]
[tex] Q = 5 \cdot 2 \cdot 0,25 \cdot 540 \cdot 30[tex]
[tex] Q = 40\ 500\ litros\ de\ água[tex]
Portanto, alternativa "E".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Uma pessoa chega ao hotel no qual fez uma pré-reserva com diária no valor de R$ 210,00. Como a confirmação da reserva não foi feita, quando chegou ao hotel não havia quarto disponível. Dessa forma, o recepcionista apresentou-lhe algumas opções de hotéis com diárias mais baratas, mas localizados a certa distância desse hotel, conforme apresentado.
• H1: diária de R$ 180,00 e distância de 7 km;
• H2: diária de R$ 200,00 e distância de 1,6 km;
• H3: diária de R$ 199,00 e distância de 4,5 km;
• H4: diária de R$ 190,00 e distância de 1,5 km;
• H5: diária de R$ 205,00 e distância de 1,2 km.
Para se locomover até um outro hotel, essa pessoa utiliza um táxi que cobra R$ 2,50 por quilômetro rodado mais taxa fixa de R$ 6,00.
Observe a tabela seguir:
| Hotel | Diária | Valor fixo | Valor variável | Total (R$) |
|---|---|---|---|---|
| H1 | 180,00 | 6,00 | 7km × 2,50 = 17,50 | 203,50 |
| H2 | 200,00 | 6,00 | 1,6km × 2,50 = 4,00 | 210,00 |
| H3 | 199,00 | 6,00 | 4,5km × 2,50 = 11,25 | 216,50 |
| H4 | 190,00 | 6,00 | 1,5km × 2,50 = 3,75 | 199,75 |
| H5 | 205,00 | 6,00 | 1,2km × 2,50 = 3,00 | 214,00 |
Portanto, esse pessoa deve escolher o Hotel 4.
Portanto, alternativa "D".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Um fazendeiro precisava de 1 L de certo produto fabricado por três indústrias distintas.
• A indústria I comercializa o produto em embalagens de 250 mL por R$ 23,00 cada.
• A indústria II comercializa o produto em embalagens de [tex]8\ fl\ oz[tex] (onça fluida) por R$ 18,50 cada.
• A indústria III comercializa o produto em embalagens de 1 L por R$ 93,00 cada.
O fazendeiro conseguiu adquirir a quantidade necessária do produto de que precisava, de uma única indústria, gastando o menor valor possível nessa compra. Considere que 1 L seja equivalente a 33,81 [tex]fl\ oz[tex].
Nessas condições, a quantidade de embalagens e a respectiva indústria onde a compra foi realizada foram
Vamos encontrar o preço do produto em cada indústria.
Primeiro converter [tex]8\ fl\ oz[tex] para litros.
[tex] 1L ----\ 33,81\ fl\ oz [tex]
[tex] x ----\ 8\ fl\ oz [tex]
[tex] x = \frac{8}{33,81} \cong 0,23671\ L[tex]
Então, serão necessários:
[tex] x = \frac{1}{0,23671} \cong 4,22\ frascos \cong 5 frascos[tex]
| Indústria | Volume | Preço unitário | Custo total |
|---|---|---|---|
| I | 1L = 4 × 250mL | R$ 23,00 | 4 × 23,00 = R$ 92,00 |
| II | 5 frascos | R$ 18,50 | 5 × 18,50 = R$ 92,50 |
| III | 1L | R$ 23,00 | R$ 93,00 |
Sendo assim, é melhor comprar o produto na indústria I.
Portanto, alternativa "A".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Para aumentar a arrecadação de seu restaurante que cobra por quilograma, o proprietário contratou um cantor e passou a cobrar dos clientes um valor fixo de couvert artístico, além do valor da comida. Depois, analisando as planilhas do restaurante, verificou-se em um dia que 30 clientes consumiram um total de 10 kg de comida em um período de 1 hora, sendo que dois desses clientes pagaram R$ 50,00 e R$ 34,00 e consumiram 500 g e 300 g, respectivamente.
Qual foi a arrecadação obtida pelo restaurante nesse período de 1 hora, em real?
Vamos equacionar o problema:
x = preço do couvert
y = preço do kg de comida
[tex] \begin{cases} x + 0,5y = 50 \\ x + 0,3y = 34 ×(-1)\end{cases} [tex]
+[tex]\underline{ \begin{cases} x + 0,5y = 50 \\ -x - 0,3y = -34 \end{cases} }[tex]
[tex]0,2y = 17 [tex]
[tex]y = \frac{16}{0,2} = R \$\ 80,00 [tex]
e
[tex]x + 0,5y = 50 [tex]
[tex]x + 0,5 \cdot 80 = 50 [tex]
[tex]x + 40 = 50 [tex]
[tex]x = 50\ -\ 40 = R \$\ 10,00 [tex]
Logo, o restaurante cobra R$ 80,00 por kg de comida e R$ 10,00 por cliente devido ao couvert Artístico.
Do enunciado: "...em um dia que 30 clientes consumiram um total de 10 kg de comida em um período de 1 hora...”.
Portanto, a arrecadação obtida pelo restaurante nesse período de 1 hora, em real, é de:
| Couvert | 30 × R$ 10,00 | R$ 300,00 |
| Alimentação | 30 × R$ 80,00 | R$ 800,00 |
| TOTAL | ------- | R$ 1 100,00 |
Portanto, alternativa "D".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Querendo reduzir custos na limpeza da área de estacionamento de um prédio, o síndico resolveu comprar uma lavadora de alta pressão. Sabe-se que, na utilização desse equipamento, o consumo de água é menor, entretanto, existe o gasto com energia elétrica. O síndico coletou os dados de cinco modelos de lavadora com mesmo preço, e cujos consumos de água e de energia são os fornecidos no quadro.
| Modelo de lavadora | Gasto médio de água (L/h) | Consumo de energia em 1 hora (kWh) |
|---|---|---|
| I | 350 | 1,3 |
| II | 264 | 2,0 |
| III | 320 | 1,5 |
| IV | 300 | 1,7 |
| V | 276 | 1,8 |
As tarifas de água e de energia elétrica são, respectivamente, R$ 0,0025 por litro de água e R$ 0,30 por quilowatt-hora.
O modelo de lavadora que o síndico deve adquirir para gastar menos com a limpeza do estacionamento é
Observe a tabela a seguir:
O modelo de lavadora que o síndico deve adquirir para gastar menos com a limpeza do estacionamento é:
= 0,0025 ∙ 350 + 1,3 ∙ 0,30 = 0,875 + 0,39 = R$ 1,265
= 0,0025 ∙ 264 + 2,0 ∙ 0,30 = 0,66 + 0,60 = R$ 1,26
= 0,0025 ∙ 320 + 1,5 ∙ 0,30 = 0,80 + 0,45 = R$ 1,25
= 0,0025 ∙ 300 + 1,7 ∙ 0,30 = 0,75 + 0,51 = R$ 1,26
= 0,0025 ∙ 276 + 1,8 ∙ 0,30 = 0,69 + 0,54 = R$ 1,23
Logo, o modelo de lavadora que o síndico deve adquirir para gastar menos com a limpeza do estacionamento é o V.
Portanto, alternativa "E".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Embora a civilização maia já estivesse em declínio na época da chegada dos espanhóis à América, seu desenvolvimento em vários campos da ciência, em especial, na matemática e na astronomia, era notável. Eles possuíam um sistema numérico avançado e diferente do sistema decimal utilizado pelas sociedades modernas.
A imagem representa o sistema de numeração maia, que consistia em 20 símbolos representando os números de 0 a 19.

IMENES, L. M. P. Os números na história da civilização. São Paulo: Editora Scipione, 2003.
O zero era representado por uma espécie de tigela e todo número inteiro entre 19 e 360 era escrito em uma coluna vertical com duas figuras, na qual a superior representava a quantidade de grupos de 20 unidades e a inferior, a quantidade de unidades. O número era lido de cima para baixo e obtido somando-se as quantidades representadas. Por exemplo:

O número 359 é representado, no sistema de numeração maia, como

Observe que o sistema numeral Maia é vigesimal. Logo:
a) [tex]17 × 20^{1} + 19 × 20^{0} = 340 + 19 = \color{Red}{359} [tex]
b) [tex]= 3 × 20^{2} + 5 × 20^{1} + 9 × 20^{0} [tex]
[tex]= 1200 + 100 + 9 = 1\ 309 [tex]
c) [tex] 1 × 20^{2} + 15 × 20^{1} + 9 × 20^{0} [tex]
[tex] = 400 + 300 + 9 = 709 [tex]
d) [tex]= 3 × 20^{2} + 2 × 20^{1} + 19 × 20^{0} [tex]
[tex] = 1\ 200 + 40 + 19 = 1\ 259 [tex]
e) [tex] 15 × 20^{2} + 2 × 20^{1} + 19 × 20^{0} [tex]
[tex] = 6\ 000 + 40 + 19 = 6\ 059 [tex]
Portanto, alternativa "A".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Um piscicultor cria uma espécie de peixe em um tanque cilíndrico. Devido às características dessa espécie, o tanque deve ter, exatamente, 2 metros de profundidade e ser dimensionado de forma a comportar 5 peixes para cada metro cúbico de água. Atualmente, o tanque comporta um total de 750 peixes. O piscicultor deseja aumentar a capacidade do tanque para que ele comporte 900 peixes, mas sem alterar a sua profundidade.
Considere 3 como aproximação para π.
O aumento da medida do raio do tanque, em metro, deve ser de
O tanque atual possui 2 metros de profundidade e comporta 5 peixes por m³ de água.
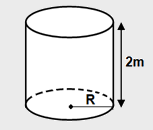
Vamos primeiro encontrar o volume do tanque original, sabendo que ele comporta 750 peixes.
5 peixes --------- 1 m³
750 peixes ----- x m³
[tex] 5x = 750 [tex]
[tex] x = \frac{750}{5} = 150\ m^{3} [tex]
Agora, é possível encontrar o raio do tanque original.
[tex] V = área\ da\ base × altura [tex]
[tex] V = π R^{2} × h [tex]
[tex] 150 = 3 R^{2} × 2 [tex]
[tex] 150 = 6 R^{2} [tex]
[tex] \frac{150}{6} = R^{2} [tex]
[tex] 25 = R^{2} [tex]
[tex] R = \sqrt{25} [tex]
[tex] R = 5\ m [tex]
Agora, encontrar o volume do novo tanque.
5 peixes --------- 1 m³
900 peixes ----- x m³
[tex] 5x = 900 [tex]
[tex] x = \frac{900}{5} = 180\ m^{3} [tex]
Também, encontrar o raio do novo tanque.
[tex] V = área\ da\ base × altura [tex]
[tex] V = π R^{2} × h [tex]
[tex] 180 = 3 R^{2} × 2 [tex]
[tex] 180 = 6 R^{2} [tex]
[tex] \frac{180}{6} = R^{2} [tex]
[tex] 30 = R^{2} [tex]
[tex] R = \sqrt{30}\ m [tex]
Então, o aumento da medida do raio do tanque, em metro, deve ser de:
[tex]\sqrt{30} - 5 [tex]
Portanto, alternativa "A".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Um imposto é dito cumulativo se incide em duas ou mais etapas da circulação de mercadorias, sem que na etapa posterior possa ser abatido o montante pago na etapa anterior. PIS e Cofins são exemplos de impostos cumulativos e correspondem a um percentual total de 3,65%, que incide em cada etapa da comercialização de um produto.
Considere um produto com preço inicial C. Suponha que ele é revendido para uma loja pelo preço inicial acrescido dos impostos descritos. Em seguida, o produto é revendido por essa loja ao consumidor pelo valor pago acrescido novamente dos mesmos impostos.
Disponível em: www.centraltributaria.com.br. Acesso em: 15 jul. 2015 (adaptado).
Qual a expressão algébrica que corresponde ao valor pago em impostos pelo consumidor?
Considere “[tex]C[tex]”, o preço inicial do produto e “[tex]i = 3,65 \%\ = 0,0365[tex]”, a taxa percentual total que incide sobre o produto.
• Valor pago pela loja:
[tex]M = C + C × i [tex]
[tex]M = C + Ci[tex]
• Valor pago pelo consumidor:
[tex] M = C + Ci + (C + Ci)i [tex]
[tex] M = C + Ci + Ci + Ci² [tex]
[tex] M = C + \color{Red}{2Ci + Ci² } [tex]
Obs. A parte em vermelho representa a parcela de impostos paga pelo consumidor.
Agora, substituindo o valor a taxa percentual “[tex]i = 0,0365[tex]“:
[tex]= 2Ci + Ci² [tex]
[tex]= 2C × 0,0365 + C × 0,0365² [tex]
[tex] = 2C × 0,0365 + C + C × 0,0365² [tex]
Portanto, alternativa "E".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Um determinado campeonato de futebol, composto por 20 times, é disputado no sistema de pontos corridos. Nesse sistema, cada time joga contra todos os demais times em dois turnos, isto é, cada time joga duas partidas com cada um dos outros times, sendo que cada jogo pode terminar empatado ou haver um vencedor.
Sabendo-se que, nesse campeonato, ocorreram 126 empates, o número de jogos em que houve ganhador é igual a
Como esse campeonato de futebol é composto por 20 times no sistema de pontos corridos com turno e returno. Como o time não joga consigo mesmo. Então, são 19 partidas no turno e mais 19 no returno.
Total de partidas de um time = 19 + 19 = 38
Em uma rodada, são 10 partidas pois são 20 times.
N° de partidas = 10 jogos × total de partidas de um time
N° de partidas = 10 × 38
N° de partidas = 380
Como ocorreram 126 empates, então o número de partidas onde houve ganhador foi de:
[tex]380\ –\ 126 = 254 [tex]
Portanto, alternativa "C".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Os alunos do curso de matemática de uma universidade desejam fazer uma placa de formatura, no formato de um triângulo equilátero, em que os seus nomes aparecerão dentro de uma região quadrada, inscrita na placa, conforme a figura.

Considerando que a área do quadrado, em que aparecerão os nomes dos formandos, mede 1 m², qual é aproximadamente a medida, em metro, de cada lado do triângulo que representa a placa?
(Utilize 1,7 como valor aproximado para [tex] \sqrt{3}[tex]).
Como o quadrado tem área de 1 m². Então, cada lado do quadrado vale 1m.
Observe a figura a seguir:

Primeiro encontrar o valor de x.
[tex] tg\ 60° = \frac{cateto\ oposto}{cateto\ adjacente} [tex]
[tex] \sqrt{3} = \frac{1}{x} [tex]
[tex]x = \frac{1}{\sqrt{3}} [tex]
[tex]x \cong \frac{1}{1,7} \cong 0,59 [tex]
Agora, encontrar a medida do lado do triângulo eqüilátero.
[tex]L = x + 1 + x [tex]
[tex]L = 0,59 + 1 + 0,59 [tex]
[tex]L = 2,18 [tex]
Portanto, alternativa "B".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Um motorista fez uma viagem de 100 km partindo da cidade A até a cidade B. Nos primeiros 30 km, a velocidade média na qual esse motorista viajou foi de 90 km/h. No segundo trecho, de 40 km, a velocidade média foi de 80 km/h. Suponha que a viagem foi realizada em 1 h 30 min.
A velocidade média do motorista, em quilômetro por hora, no último trecho da viagem foi de
Observe o esquema a seguir:

Calcular o tempo no primeiro trecho:
[tex] v_{m} = \frac{Δs}{Δt} [tex]
[tex] 90 = \frac{30}{Δt} [tex]
[tex] Δt = \frac{30}{90} = \frac{1}{3} h = 20 min[tex]
Também, calcular o tempo no segundo trecho:
[tex] v_{m} = \frac{Δs}{Δt} [tex]
[tex] 80 = \frac{40}{Δt} [tex]
[tex] Δt = \frac{40}{80} = \frac{1}{2} h = 30 min[tex]
Agora, o tempo no terceiro trecho:
[tex] 20 min + 30 min + t = 1h30min [tex]
[tex]t = 90 min - 50min [tex]
[tex]t = 40 min = \frac{40}{60}h = \frac{2}{3}h[tex]
Por último encontrar a velocidade média no último trecho.
[tex] v_{m} = \frac{Δs}{Δt} [tex]
[tex] v_{m} = \frac{30km}{\frac{2}{3}h} = 30 \cdot \frac{3}{2}\frac{km}{h} [tex]
[tex] v_{m} = \frac{90km}{2h} = 45\ km/h [tex]
Portanto, alternativa "A".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
A taxa de mortalidade infantil vem decaindo a cada ano no Brasil. O gráfico, gerado a partir de dados do IBGE, apresenta a evolução da taxa de mortalidade infantil (número de óbitos para cada 1 000 nascidos vivos) de crianças com até 5 anos, no Brasil, no período de 2000 a 2011.

Considere que, para os próximos anos, o decréscimo anual médio do número de óbitos para cada 1 000 nascidos vivos registrado, no período de 2009 a 2011, será mantido.
A partir das informações fornecidas, a taxa de mortalidade infantil de crianças com até 5 anos tornar-se-á inferior a 10 no período de
(ENEM 2020 - 2ª Aplicação).
Um estudante, morador da cidade de Contagem, ouviu dizer que nessa cidade existem ruas que formam um hexágono regular. Ao pesquisar em um sítio de mapas, verificou que o fato é verídico, como mostra a figura.

Disponível em: www.google.com. Acesso em: 7 dez. 2017 (adaptado).
Ele observou que o mapa apresentado na tela do computador estava na escala 1 : 20 000. Nesse instante, mediu o comprimento de um dos segmentos que formam os lados desse hexágono, encontrando 5 cm.
Se esse estudante resolver dar uma volta completa pelas ruas que formam esse hexágono, ele percorrerá, em quilômetro,
Vamos encontrar o comprimento de uma rua, que faz parte do hexágono regular, sabendo que no mapa tem 5 cm e que a escala adotada é de 1: 20 000. Logo:
mapa real
[tex]1\ cm ----\ 20\ 000\ cm = 200\ m[tex]
[tex]5\ cm ---- \ x\ m[tex]
[tex]x = 5 \cdot 200 [tex]
[tex]x = 1\ 000\ m = 1\ km [tex]
Agora, encontrar o valor de uma volta neste hexágono:
[tex]1\ volta = 6 × 1\ km = 6\ km [tex]
Portanto, alternativa "C".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
A prefeitura de uma cidade está renovando os canteiros de flores de suas praças. Entre as possíveis variedades que poderiam ser plantadas, foram escolhidas cinco: amor-perfeito, cravina, petúnia, margarida e lírio. Em cada um dos canteiros, todos com composições diferentes, serão utilizadas somente três variedades distintas, não importando como elas serão dispostas.
Um funcionário deve determinar os trios de variedades de flores que irão compor cada canteiro.
De acordo com o disposto, a quantidade de trios possíveis é dada por
Como tem 5 variedades de flores e que as 3 que irão ser plantadas em cada canteiro não importando como elas serão dispostas. Isso caracteriza uma combinação simples. Sendo assim,
[tex]p = 5[tex] variedades de flores
[tex]n = 3[tex] variedades que irá compor cada canteiro.
[tex] \frac{5!}{(5\ -3)!\ 3!} [tex]
Portanto, alternativa "E".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Uma formiga move-se sobre um castiçal de vidro transparente, do ponto A para B em linha reta, percorre o arco circular BCD, sendo C localizado na parte da frente do castiçal, e desce o arco DE, como representado na figura.

Os pontos A, B, D e E estão sobre um mesmo plano perpendicular à mesa sobre a qual se encontra o castiçal.
A projeção ortogonal, sobre o plano da mesa, do trajeto percorrido pela formiga, do ponto A até o ponto E, é melhor representada por

(ENEM 2020 - 2ª Aplicação).
Um reservatório de água é abastecido por uma torneira ao mesmo tempo que, por um ralo, escoa água de seu interior. Os gráficos representam as vazões Q, em litro por minuto, da torneira e do ralo, em função do tempo t, em minuto.
Nos primeiros 25 minutos, o(s) intervalo(s) de tempo em que o volume de água nesse reservatório decresce é(são)
O volume de água vai decrescer quando o volume de água que sair do ralo foi maior que o volume de água que entra pela torneira.
E isso é constatado no intervalo de 15 min até 25 min.
Portanto, alternativa "B".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Dois atletas partem de pontos, respectivamente [tex]P_{1}[tex] e [tex]P_{2}[tex], em duas pistas planas distintas, conforme a figura, deslocando-se no sentido anti-horário até a linha de chegada, percorrendo, desta forma, a mesma distância (L). Os trechos retos dos finais das curvas até a linha de chegada desse percurso têm o mesmo comprimento (l) nas duas pistas e são tangentes aos trechos curvos, que são semicírculos de centro C. O raio do semicírculo maior é [tex]R_{1}[tex] e o raio do semicírculo menor é [tex]R_{2}[tex].

Sabe-se que o comprimento de um arco circular é dado pelo produto do seu raio pelo ângulo, medido em radiano, subentendido pelo arco.
Nas condições apresentadas, a razão da medida do ângulo [tex]P_{2} \hat{C}P_{1} [tex] pela diferença [tex]L\ −\ l[tex] é dada por
Vamos ilustrar os arcos [tex]S_{1}[tex] e [tex]S_{2}[tex] do percurso (L) de cada corredor:

Como os atletas percorrem a mesma distância L, então temos que:
[tex] L = I + S_{1} e L = I + S_{2} [tex]
Logo:
[tex]S_{1} = S_{2}[tex]
Sendo assim:
[tex] α \cdot R_{1} = (α + θ) \cdot R_{2} [tex]
[tex] α R_{1} = αR_{2} + θR_{2} [tex]
[tex] α R_{1}\ -\ αR_{2} = θR_{2} [tex]
[tex] \frac{αR_{1}\ -\ αR_{2}}{R_{2}} = θ [tex]
Como o objetivo da questão é calcular:
[tex] \frac{θ}{L\ -\ I} [tex]
A expressão [tex](L\ –\ I)[tex] vale [tex]S_{1}[tex], veja:
[tex]L = I + S_{1} → L\ –\ I = S1[tex]
Finalmente basta dividir:
[tex] =\frac{θ}{S_{1}} [tex]
[tex]=\frac{\frac{αR_{1}\ -\ αR_{2}}{R_{2}}}{α\ \cdot\ R_{1}} [tex]
[tex]= \frac{αR_{1}\ -\ αR_{2}}{R_{2}}\ \cdot\ \frac{1}{α\ \cdot\ R_{1}} [tex]
[tex]= \frac{αR_{1}\ -\ αR_{2}}{R_{2}\ \cdot\ α\ \cdot R_{1}} [tex]
[tex]= \frac{α(R_{1}\ -\ R_{2})}{R_{2}\ \cdot\ α\ \cdot R_{1}} [tex]
[tex]= \frac{R_{1}\ -\ R_{2}}{R_{2}\ \cdot\ R_{1}} [tex]
[tex]= \frac{R_{1}}{R_{2}\ \cdot\ R_{1}} - \frac{R_{2}}{R_{2}\ \cdot\ R_{1}} [tex]
[tex]= \frac{1}{R_{2}} - \frac{1}{R_{1}} [tex]
Portanto, alternativa "C".
(Fonte da resolução: ∑exercícios resolvidos.)
(ENEM 2020 - 2ª Aplicação).
Foi feita uma pesquisa sobre a escolaridade dos funcionários de uma empresa. Verificou-se que [tex] \frac{1}{4}[tex] dos homens que ali trabalham têm o ensino médio completo, enquanto [tex] \frac{2}{3}[tex] das mulheres que trabalham na empresa têm o ensino médio completo. Constatou-se, também, que entre todos os que têm o ensino médio completo, metade são homens.
A fração que representa o número de funcionários homens em relação ao total de funcionários dessa empresa é
De acordo com o enunciado vamos considerar:
• [tex]X[tex] = quantidade de funcionários (sexo masculino);
• [tex] Y[tex] = quantidade de funcionárias (sexo feminino);
• [tex]X\ +\ Y[tex] = quantidade de funcionários no total (ambos os sexos);
• [tex] \frac{1}{4}[tex] são homens com Ensino Médio.
• [tex] \frac{2}{3}[tex] são mulheres com Ensino Médio.
• Queremos encontrar: [tex] \frac{X}{X\ +\ Y}[tex].
De acordo com o enunciado, todos que tem ensino médio completo, metade são homens. Isso significa que o restante são mulheres.
Então, podemos concluir que:
[tex] \frac{1}{4} \cdot X = \frac{2}{3} \cdot Y [tex]
[tex] X = \frac{\frac{2}{3}}{\frac{1}{4}} \cdot Y [tex]
[tex] X = \frac{2}{3} \cdot \frac{4}{1} \cdot Y [tex]
[tex] X = \frac{8}{3} \cdot Y [tex]
Por último, basta calcular o objetivo do problema:
[tex]= \frac{X}{X\ +\ Y}[tex]
[tex]= \frac{\frac{8}{3} \cdot Y}{\frac{8}{3} \cdot Y\ +\ Y}[tex]
[tex]= \frac{\frac{8}{3} \cdot Y}{Y (\frac{8}{3} + 1)}[tex]
[tex]= \frac{\frac{8}{3}}{\frac{8}{3}\ +\ 1} [tex]
[tex]= \frac{\frac{8}{3}}{\frac{8}{3}\ +\ \frac{3}{3}} [tex]
[tex]= \frac{\frac{8}{3}}{\frac{11}{3}} [tex]
[tex]= \frac{8}{3} \cdot \frac{3}{11} [tex]
[tex]= \frac{8}{11} [tex]
Portanto, alternativa "E".
(Fonte da resolução: ∑exercícios resolvidos.)
(ENEM 2020 - 2ª Aplicação).
Para um docente estrangeiro trabalhar no Brasil, ele necessita validar o seu diploma junto ao Ministério da Educação. Num determinado ano, somente para estrangeiros que trabalharão em universidades dos estados de São Paulo e Rio de Janeiro, foram validados os diplomas de 402 docentes estrangeiros. Na tabela, está representada a distribuição desses docentes estrangeiros, por países de origem, para cada um dos dois estados.
| São Paulo | Rio de Janeiro | Total | |
|---|---|---|---|
| Argentina | 112 | 29 | 141 |
| Espanha | 60 | 40 | 100 |
| Cuba | 28 | 46 | 74 |
| Portugal | 9 | 36 | 45 |
| Venezuela | 30 | 12 | 42 |
| Total de docentes | 239 | 163 | 402 |
A probabilidade de se escolher, aleatoriamente, um docente espanhol, sabendo-se que ele trabalha em uma universidade do estado de São Paulo é
A probabilidade de se escolher, aleatoriamente, um docente espanhol, sabendo-se que ele trabalha em uma universidade do estado de São Paulo é de:
[tex] P = \frac{Evento}{Espaço\ amostral} [tex]
[tex] P = \frac{Quant.\ de\ Espanhol\ que\ trabalha\ em\ SP}{Total\ de\ docentes\ em\ SP} [tex]
[tex] P = \frac{60}{239} [tex]
Portanto, alternativa "B".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Um vidraceiro precisa construir tampos de vidro com formatos diferentes, porém com medidas de áreas iguais. Para isso, pede a um amigo que o ajude a determinar uma fórmula para o cálculo do raio R de um tampo de vidro circular com área equivalente à de um tampo de vidro quadrado de lado L.

A fórmula correta é
(ENEM 2020 - 2ª Aplicação).
Um professor pediu aos seus alunos que esboçassem um gráfico representando a relação entre metro cúbico e litro, utilizando um software. Pediu ainda que representassem graficamente os pontos correspondentes às transformações de 0 m³, 2 m³ e 4 m³ em litro.
O professor recebeu de cinco alunos os seguintes gráficos:
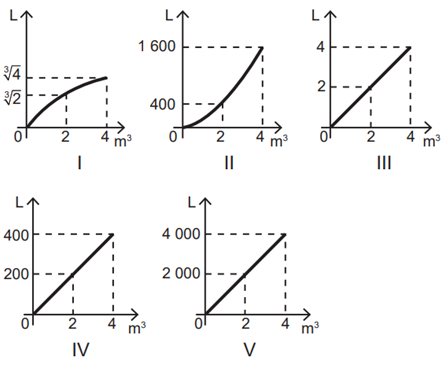
O gráfico que melhor representa o esboço da transformação de metro cúbico para litro é o do aluno
Como [tex]1\ m³ = 1\ 000\ litros[tex]. Logo, o aluno que construiu o gráfico V fez corretamente. Pois:
[tex]2\ m³ = 2\ 000\ Litros [tex]
[tex] 4\ m³ = 4\ 000\ Litros [tex]
Portanto, alternativa "E".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
O nanofio é um feixe de metais semicondutores usualmente utilizado na fabricação de fibra óptica. A imagem ilustra, sem escala, as representações das medidas dos diâmetros de um nanofio e de um fio de cabelo, possibilitando comparar suas espessuras e constatar o avanço das novas tecnologias.

O número que expressa a razão existente entre o comprimento do diâmetro de um fio de cabelo e o de um nanofio é
A razão existente entre o comprimento do diâmetro de um fio de cabelo e o de um nanofio é:
[tex]razão = \frac{diâmetro\ do\ fio\ de\ cabelo}{diâmetro\ do\ nanofio} [tex]
[tex]razão = \frac{6\ ×\ 10^{-5}}{10^{-9}} [tex]
[tex]razão = 6 × 10^{-5-(-9)} [tex]
[tex]razão = 6 × 10^{-5+9} [tex]
[tex]razão = 6 × 10^{4} [tex]
Portanto, alternativa "D".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Projetado pelo arquiteto Oscar Niemeyer, o Museu de Arte Contemporânea (MAC) tornou-se um dos cartões-postais da cidade de Niterói (Figura 1).

Figura 1
Considere que a forma da cúpula do MAC seja a de um tronco de cone circular reto (Figura 2), cujo diâmetro da base maior mede 50 m e 12 m é a distância entre as duas bases. A administração do museu deseja fazer uma reforma revitalizando o piso de seu pátio e, para isso, precisa estimar a sua área.
(Utilize 1,7 como valor aproximado para [tex]\sqrt{3} [tex] e 3 para π).

Figura 2
A medida da área do pátio do museu a ser revitalizada, em metro quadrado, está no intervalo
Observe a figura a seguir:

Agora, encontrar o Raio do piso do pátio (R).
[tex]tg\ 60º = \frac{cateto\ oposto}{cateto\ adjacente}[tex]
[tex]\sqrt{3} = \frac{12}{x}[tex]
[tex]x = \frac{12}{\sqrt{3}}[tex]
[tex]x \cong \frac{12}{1,7}[tex]
[tex] x \cong 7\ m [tex]
Sabendo que [tex]R = 25\ -\ x [tex], temos:
[tex]R = 25\ -\ x [tex]
[tex]R = 25\ -\ 7 [tex]
[tex]R = 18\ m [tex]
Como o piso do pático é circular. Logo, a área é:
[tex] Área = π\ R^{2} [tex]
[tex] Área = 3 \cdot 18^{2} [tex]
[tex] Área = 3 \cdot 324 [tex]
[tex] Área = 972\ m^{2} [tex]
Portanto, alternativa "D".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Se a tartaruga, a lesma e o caramujo apostassem uma corrida, a lesma chegaria em último lugar, o penúltimo colocado seria o caramujo e a primeira seria a tartaruga. Segundo o biólogo americano Branley Allan Branson, a velocidade “recorde” já registrada em pesquisas, por uma lesma, é de 16,5 centímetros por minuto.
Disponível em: http://mundoestranho.abril.com.br. Acesso em: 6 jul. 2015.
Para uma reportagem, dispondo das velocidades recordes da tartaruga e do caramujo em metro por segundo, se faz necessário saber o fator de conversão da velocidade recorde da lesma para metro por segundo para divulgar uma comparação.
Com base nas informações, o fator de conversão da velocidade recorde da lesma para metro por segundo é
Como a velocidade “recorde” da lesma, é de 16,5 centímetros por minuto. Essa velocidade em metros por segundo é:
[tex] V = 16,5\ {\color{Red}{\frac{cm}{min}}} [tex]
[tex] V = 16,5\ \frac{{\color{Red}{10^{-2}}}\ m}{{\color{Red}{60}}\ s} [tex]
[tex] V = 16,5\ \frac{{\color{Red}{10^{-2}}}}{{\color{Red}{60}}}\ \cdot\ m/s [tex]
[tex] V = 16,5\ \cdot ({\color{Red}{10^{-2} × 60^{-1}}})\ \cdot\ m/s [tex]
Portanto, alternativa "B".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Um síndico precisa pintar os muros, portões e calçamento de um edifício. Os pintores solicitaram três galões de tinta T1 para os muros, um galão de tinta T2 para os portões e dois galões de tinta T3 para o calçamento. Ele pesquisou o preço das tintas em cinco lojas diferentes, obtendo os seguintes valores, em real.
| Loja | T1 | T2 | T3 |
|---|---|---|---|
| 1 | 82,00 | 134,00 | 202,00 |
| 2 | 80,00 | 122,00 | 214,00 |
| 3 | 85,00 | 115,00 | 209,00 |
| 4 | 88,00 | 132,00 | 199,00 |
| 5 | 90,00 | 116,00 | 202,00 |
O síndico irá comprar as tintas numa única loja, escolhendo aquela em que o valor total da compra resulte no menor preço médio por galão.
Com base nessas informações, a loja escolhida será
Observe a tabela a seguir:
| Loja | Total |
|---|---|
| 1 | = 82 ∙ 3 + 134 ∙ 1 + 202 ∙ 2 = 246 + 134 + 404 = 784,00 |
| 2 | = 80 ∙ 3 + 122 ∙ 1 + 214 ∙ 2 = 240 + 122 + 428 = 790,00 |
| 3 | = 85 ∙ 3 + 115 ∙ 1 + 209 ∙ 2 = 255 + 115 + 418 = 788,00 |
| 4 | = 88 ∙ 3 + 132 ∙ 1 + 199 ∙ 2 = 264 + 132 + 398 = 794,00 |
| 5 | = 90 ∙ 3 + 116 ∙ 1 + 202 ∙ 2 = 270 + 116 + 404 = 790,00 |
Portanto, alternativa "A".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
A fim de reforçar o orçamento familiar, uma dona de casa começou a produzir doces para revender. Cada receita é composta de [tex] \frac{4}{5} [tex] de quilograma de amendoim e [tex] \frac{1}{5} [tex] de quilograma de açúcar.
O quilograma de amendoim custa R$ 10,00 e o do açúcar, R$ 2,00. Porém, o açúcar teve um aumento e o quilograma passou a custar R$ 2,20. Para manter o mesmo custo com a produção de uma receita, essa dona de casa terá que negociar um desconto com o fornecedor de amendoim.
Nas condições estabelecidas, o novo valor do quilograma de amendoim deverá ser igual a
Vamos equacionar o problema:
Primeiro iremos encontrar o preço inicial da receita (R).
[tex] R = \frac{4}{5} \cdot 10,00 + \frac{1}{5} \cdot 2,00 [tex]
[tex] R = \frac{40,00}{5} + \frac{2,00}{5} [tex]
[tex] R = \frac{42,00}{5} = R \$\ 8,40 [tex]
Agora, considerando que houve um aumento do preço do quilograma do açúcar para R$ 2,20. Então, precisamos encontrar o novo preço do quilograma de amendoim, de modo a manter o preço de R$ 8,40.
[tex] 8,40 = \frac{4}{5} \cdot y + \frac{1}{5} \cdot 2,20 [tex]
[tex] 8,40 = \frac{4y}{5} + \frac{2,20}{5} [tex]
[tex] 8,40 = \frac{4y\ +\ 2,20}{5} [tex]
[tex] 4y + 2,20 = 8,40 \cdot 5 [tex]
[tex] 4y = 42,00 - 2,20 [tex]
[tex] 4y = 39,80[tex]
[tex] y = \frac{39,80}{4} [tex]
[tex] y = R \$\ 9,95 [tex]
Portanto, alternativa "E".
(Fonte da resolução: Prof. Warles.)
(ENEM 2020 - 2ª Aplicação).
Uma pesquisa de mercado sobre produtos de higiene e limpeza apresentou o comparativo entre duas marcas, A e B. Esses produtos são concentrados e, para sua utilização, é necessária sua diluição em água. O quadro apresenta a comparação em relação ao preço dos produtos de cada marca e ao rendimento de cada produto em litro.
| Produtos | Preço Marca (A) | Preço Marca (B) | Rendimento Marca (A) | Rendimento Marca (B) |
|---|---|---|---|---|
| Sabão líquido concentrado (1L) | R$ 6,00 | R$ 5,10 | 3 L | 2,5 L |
| Alvejante concentrado (1L) | R$ 4,50 | R$ 3,00 | 12 L | 9 L |
| Amaciante concentrado (1L) | R$ 4,50 | R$ 5,00 | 7 L | 6 L |
| Detergente concentrado (1L) | R$ 1,60 | R$ 2,20 | 3 L | 4 L |
Um consumidor pretende comprar um litro de cada produto e para isso escolherá a marca com o menor custo em relação ao rendimento.
Nessas condições, as marcas dos quatro produtos adquiridos pelo consumidor, na ordem apresentada na tabela, são
Observe as tabelas a seguir:
| Sabão líquido concentrado (1L) | Menor preço | |
|---|---|---|
| Marca A | [tex]\frac{Preço}{Rendimento} = \frac{6,00}{3\ L} = 2,00\ R \$\ /L [tex] | Marca "A" |
| Marca B | [tex]\frac{Preço}{Rendimento} = \frac{5,10}{2,5\ L} = 2,04\ R \$\ /L [tex] | |
| Alvejante concentrado (1L) | Menor preço | |
|---|---|---|
| Marca A | [tex]\frac{Preço}{Rendimento} = \frac{4,50}{12\ L} = 0,38\ R \$\ /L [tex] | Marca "B" |
| Marca B | [tex]\frac{Preço}{Rendimento} = \frac{3,00}{9\ L} = 0,33\ R \$\ /L [tex] | |
| Amaciante concentrado (1L) | Menor preço | |
|---|---|---|
| Marca A | [tex]\frac{Preço}{Rendimento} = \frac{4,50}{7\ L} = 0,64\ R \$\ /L [tex] | Marca "A" |
| Marca B | [tex]\frac{Preço}{Rendimento} = \frac{5,00}{6\ L} = 0,83\ R \$\ /L [tex] | |
| Detergente concentrado (1L) | Menor preço | |
|---|---|---|
| Marca A | [tex]\frac{Preço}{Rendimento} = \frac{1,60}{3\ L} = 0,53\ R \$\ /L [tex] | Marca "A" |
| Marca B | [tex]\frac{Preço}{Rendimento} = \frac{2,20}{4\ L} = 0,55\ R \$\ /L [tex] | |
Logo, as marcas dos quatro produtos adquiridos pelo consumidor, na ordem apresentada na tabela, são: A, B, A, A.
Portanto, alternativa "B".
(Fonte da resolução: Prof. Warles.)

Nenhum comentário:
Postar um comentário