(ENEM 2018 - 2ª Aplicação).
De acordo com a Organização Mundial de Saúde (OMS), o limite de ruído suportável para o ouvido humano é de 65 decibéis. Ruídos com intensidade superior a este valor começam a incomodar e causar danos ao ouvido. Em razão disto, toda vez que os ruídos oriundos do processo de fabricação de peças em uma fábrica ultrapassam este valor, é disparado um alarme sonoro, indicando que os funcionários devem colocar proteção nos ouvidos. O gráfico fornece a intensidade sonora registrada no último turno de trabalho dessa fábrica. Nele, a variável t indica o tempo (medido em hora), e I indica a intensidade sonora (medida em decibel).

Disponível em: www.cmariocovas.sp.gov.br. Acesso em: 24 abr. 2015 (adaptado)
De acordo com o gráfico, quantas vezes foi necessário colocar a proteção de ouvidos no último turno de trabalho?
Pelo gráfico, constatamos 3 vezes a necessidade de utilizar os fones de ouvidos.

(ENEM 2018 - 2ª Aplicação).
Usando a capacidade máxima de carga do caminhão de uma loja de materiais de construção, é possível levar 60 sacos de cimento, ou 90 sacos de cal, ou 120 latas de areia. No pedido de um cliente, foi solicitada a entrega de 15 sacos de cimento, 30 sacos de cal e a maior quantidade de latas de areia que fosse possível transportar, atingindo a capacidade máxima de carga do caminhão.
Nessas condições, qual a quantidade máxima de latas de areia que poderão ser enviadas ao cliente
Encontrando a razão entre a quantidade de cimento e cal em relação a quantidade de latas de areia. Logo,
[tex] \frac{60\ sacos\ de\ cimento}{120\ latas\ de\ areia} = \frac{90\ sacos\ de\ cal}{120\ latas\ de\ areia} [tex]
ou
[tex] \frac{1\ saco\ de\ cimento}{2\ latas\ de\ areia} = \frac{3\ sacos\ de\ cal}{4\ latas\ de\ areia} [tex]
Portanto,
[tex] \frac{1\ saco\ de\ cimento}{2\ latas\ de\ areia} = \frac{15\ sacos\ de\ cal}{30\ latas\ de\ areia} [tex]
e
[tex] \frac{3\ sacos\ de\ cimento}{4\ latas\ de\ areia} = \frac{30\ sacos\ de\ cal}{40\ latas\ de\ areia} [tex]
Sendo assim,
30 + 40 = 70 latas
Como no caminhão transporta no máximo 120 latas de areia.
Logo, 120 - 70 = 50 latas de areia.
(ENEM 2018 - 2ª Aplicação).
Ao acessar uma página da internet, que trata da pesquisa de assuntos de interesse juvenil, encontramos a figura:

Sabe-se que nesse tipo de comunicação visual, comum em páginas da internet, o tamanho das letras está diretamente associado ao número de vezes que o assunto ou termo foi pesquisado ou lido naquela página. Dessa forma, quanto maior o tamanho das letras de cada palavra, maior será o número de vezes que esse tema foi pesquisado.
De acordo com a figura, quais são, em ordem decrescente, os três assuntos que mais interessaram às pessoas que acessaram a página citada?
Como o tamanho das letras está diretamente associado ao número de vezes que o assunto ou termo foi pesquisado ou lido naquela página. Logo, ordem decrescente, os assuntos são:
AMOR - BALADAS E MÚSICA

(ENEM 2018 - 2ª Aplicação).
Uma empresa de construção comprou um terreno de formato retangular por R$ 700 000,00. O terreno tem 90 m de comprimento e 240 m de largura. O engenheiro da empresa elaborou três projetos diferentes para serem avaliados pela direção da construção, da seguinte maneira:
Projeto 1: dividir o terreno em lotes iguais de 45 m x 10 m, sem ruas entre os lotes, e vender cada lote por R$ 23 000,00;
Projeto 2: dividir o terreno em lotes iguais de 20 m x 30 m, deixando entre lotes ruas de 10 m de largura e 240 m de comprimento, e vender cada lote por R$ 35 000,00;
Projeto 3: dividir o terreno em lotes iguais de 35 m x 20 m, deixando entre lotes ruas de 20 m de largura e 240 m de comprimento, e vender cada lote por R$ 45 000,00.
A direção da empresa decidiu dividir o terreno e utilizar o projeto que permitirá o maior lucro, sendo que este será igual ao valor obtido pela venda dos lotes, menos o valor da compra do terreno.
Nesse caso, o lucro da construtora, em real, será de
O terreno retangular tem área igual a:
área = comp. × largura = 90 × 240 = 21 600 m²
[tex] Lucro:\ \frac{21600}{(45\ \cdot 10)}\ \cdot 23\ 000,00\ =\ \frac{21\ 600}{450}\ \cdot 23\ 000,00\ [tex]
[tex] = 48\ \cdot 23\ 000,00 = R \$\ 1\ 104\ 000,00 [tex]
Portanto, R$ 1 104 000 - R$ 700 000 = R$ 404 000,00
Projeto 2: Como as ruas tem 10 m de largura. Logo, em 90 m terá 3 ruas de 10 m e 3 quadras de 20 m de comprimento.
[tex] Lucro:\ \frac{3(20\ \cdot 240)}{(20\ \cdot 30)}\ \cdot 35\ 000,00\ =\ \frac{14\ 400}{600}\ \cdot 35\ 000,00\ [tex]
[tex] = 24\ \cdot 35\ 000,00 = R \$\ 840\ 000,00 [tex]
Portanto, R$ 840 000 - R$ 700 000 = R$ 140 000,00
Projeto 3: Como as ruas tem 20 m de largura. Logo, em 90 m terá 1 rua de 20 m e 2 quadras de 35 m.
[tex] Lucro:\ \frac{2(35\ \cdot 240)}{(35\ \cdot 20)}\ \cdot 45\ 000,00\ =\ \frac{16\ 800}{700}\ \cdot 45\ 000,00\ [tex]
[tex] = 24\ \cdot 45\ 000,00 = R \$\ 1\ 080\ 000,00 [tex]
Portanto, R$ 1 080 000 - R$ 700 000 = R$ 380 000,00
Logo, o maior lucro será de R$ 404 000,00
(ENEM 2018 - 2ª Aplicação).
Uma torneira do tipo 1/4 de volta é mais econômica, já que seu registro abre e fecha bem mais rapidamente do que o de uma torneira comum. A figura de uma torneira do tipo 1/4 de volta tem um ponto preto marcado na extremidade da haste de seu registro, que se encontra na posição fechado, e, para abri-lo completamente, é necessário girar a haste 1/4 de volta no sentido anti-horário. Considere que a haste esteja paralela ao plano da parede.
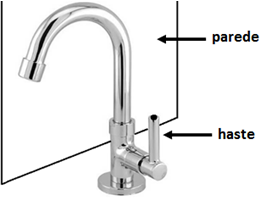
Disponível em: www.furkin.com.br. Acesso em: 13 nov. 2014
Qual das imagens representa a projeção ortogonal, na parede, da trajetória traçada pelo ponto preto quando o registro é aberto complemente

Como a abertura da torneira é de 1/4 de volta. Logo, a projeção será o arco de 90°. Portanto, opção A.
(ENEM 2018 - 2ª Aplicação).
Um torrefador comprou uma saca de 60 kg de café especial cru (antes de torrar) por R$ 400,00. Devido à perda de umidade durante o processo de torrefação, são perdidos 10 kg de café por saca.
O torrefador irá vender o café torrado em embalagens de um quilograma e tem por objetivo obter um lucro de 200%, em relação ao valor pago, por unidade vendida.
Que preço de venda, por unidade, este torrefador deverá estabelecer para atingir o seu objetivo?
Cálculo do preço do kg do café torrado:
[tex] \frac{R\$\ 400,00}{50\ kg} = R \$\ 8,00 [tex]
Como deve ter um lucro de 200% = 2, logo:
R$ 8,00 x 200% = 8,00 x 2 = R$ 16,00
Logo, o preço de venda é:
Preço de venda = Custo de produção + Lucro
Preço de venda = 8,00 + 16,00 = R$ 24,00
(ENEM 2018 - 2ª Aplicação).
Na intenção de ampliar suas fatias de mercado, as operadoras de telefonia apresentam diferentes planos e promoções. Uma operadora oferece três diferentes planos baseados na quantidade de minutos utilizados mensalmente, apresentados no gráfico. Um casal foi à loja dessa operadora para comprar dois celulares, um para a esposa e outro para o marido. Ela utiliza o telefone, em média, 30 minutos por mês, enquanto ele, em média, utiliza 90 minutos por mês.

Com base nas informações do gráfico, qual é o plano de menor custo mensal para cada um deles?

Pelo gráfico, obtemos que o melhor plano para a esposa (30 min) é o C e para o marido que utiliza em média 90 min por mês é o plano B.
(ENEM 2018 - 2ª Aplicação).
No quadro estão representados as quantidades de certos tipos de vinho vendidos durante um ano e o lucro por unidade vendida de cada um desses tipos. Para repor seu estoque, o proprietário escolherá apenas os tipos de vinho em que o lucro total com sua venda foi maior do que a média entre os lucros obtidos com a venda de todos os tipos.

Conforme condições estabelecidas, os tipos de vinho escolhidos serão
Calculando a média do lucro de cada vinho:
Vinho I: Lucro total= 120∙6= R$ 720,00
Vinho II: Lucro total= 50∙12= R$ 600,00
Vinho III: Lucro total= 71∙10= R$ 710,00
Vinho IV: Lucro total= 47∙20= R$ 940,00
Vinho V: Lucro total= 70∙5= R$ 350,00
Vinho VI: Lucro total= 90∙12= R$ 1 080,00
Calculando a média do lucro total:
[tex] média = \frac{720+600+710+940+350+1080}{6} = \frac{4400}{6} \cong 733,33 [tex]
Portanto, os tipos de vinho escolhidos serão os IV e VI.
(ENEM 2018 - 2ª Aplicação).
Para pintar um automóvel, cuja cor é personalizada, a oficina encarregada de fazer o serviço terá de, por meio de uma mistura adequada de tintas, compor tons de azul e de branco. O tom azul representa 40% dessa mistura.
Sabe-se, ainda, que a oficina deverá adquirir somente a tinta de tom azul, pois já possui, em seus estoques, 6 litros da tinta de tom branco, que serão totalmente utilizados na referida composição.
A quantidade, em litro, de tinta de tom azul que a oficina deverá adquirir para compor essa mistura, sem que haja sobras, é
Como a quantidade de tinta branca corresponde a 60% e que isso corresponde a 6 litros. Portanto, a quantidade de tintas azul que deve ser comprada é de 40%, ou seja, 4 litros.
(ENEM 2018 - 2ª Aplicação).
Uma pessoa possui um terreno em forma de um pentágono, como ilustrado na figura.

Sabe-se que a diagonal AD mede 50 m e é paralela ao lado BC, que mede 29 m. A distância do ponto B a AD é de 8 m e a distância do ponto E a AD é de 20 m.
A área, em metro quadrado, deste terreno é igual a

A área do terreno é dado por:
[tex] Área\ do\ terreno = A_{trapézio}\ +\ A_{triângulo} [tex]
[tex] Área\ do\ terreno = \frac{(B\ +\ b)h}{2}\ +\ \frac{b \ \cdot\ h}{2} [tex]
[tex] Área\ do\ terreno = \frac{(50\ +\ 29)8}{2}\ +\ \frac{50 \ \cdot\ 20}{2} [tex]
[tex] Área\ do\ terreno = 79\ \cdot 4 +\ 50\ \cdot\ 10 [tex]
[tex] Área\ do\ terreno = 316\ +\ 500 [tex]
[tex] Área\ do\ terreno = 816\ m^{2} [tex]
(ENEM 2018 - 2ª Aplicação).
A Lei da Gravitação, de Isaac Newton, estabelece a intensidade da força entre dois objetos. Ela é dada pela equação [tex] F = g\ \cdot \frac{m_{1}\ \cdot\ m_{2}}{d^{2}} [tex], sendo [tex] m_{1}[tex] e [tex] m_{2}[tex] as massas dos objetos, d a distância entre eles, g a constante universal da gravitação e F a intensidade da força gravitacional que um objeto exerce sobre o outro.
Considere um esquema que represente cinco satélites de mesma massa orbitando a Terra. Denote os satélites por A, B, C, D e E, sendo esta a ordem decrescente da distância da Terra (A o mais distante e E o mais próximo da Terra).
De acordo com a Lei de Gravitação Universal, a Terra exerce maior força sobre o satélite
Pela Lei da Gravitação, de Isaac Newton, [tex] F = g\ \cdot \frac{m_{1}\ \cdot\ m_{2}}{d^{2}} [tex] , temos as massas, [tex]m_{1}[tex] e [tex]m_{2}[tex] são diretamente proporcionais e a distância inversamente proporcional.
Logo, quanto menor a distância entre a Terra e o satélite, maior a força de interação.
(ENEM 2018 - 2ª Aplicação).
A inclinação de um telhado depende do tipo e da marca das telhas escolhidas. A figura é o esboço do telhado da casa de um específico proprietário. As telhas serão apoiadas sobre a superfície quadrada plana ABCD, sendo BOC um triângulo retângulo em O. Sabe-se que h é a altura do telhado em relação ao forro da casa (a figura plana ABOE), b = 10 é o comprimento do segmento OB, e d é a largura do telhado (segmento AB), todas as medidas dadas em metro.

Disponível em: www.toptelha.com.br. Acesso em: 31 jul. 2012.
Sabe-se que, em função do tipo de telha escolhida pelo proprietário, a porcentagem i de inclinação ideal do telhado, descrita por meio da relação [tex]i\ = \frac{h\ \cdot\ 100}{b}[tex] , é de 40%, e que a expressão que determina o número N de telhas necessárias na cobertura é dada por [tex] N\ =\ d^{2}\ \cdot\ 10,5[tex] . Além disso, essas telhas são vendidas somente em milheiros.
O proprietário avalia ser fundamental respeitar a inclinação ideal informada pelo fabricante, por isso argumenta ser necessário adquirir a quantidade mínima de telhas correspondente a
Encontrando a altura h, sendo a inclinação é 40%.
[tex] i\ = \frac{h\ \cdot\ 100}{b}[tex]
[tex] 40\ = \frac{h\ \cdot\ 100}{10}[tex]
[tex] 100h\ =\ 400 [tex]
[tex]h\ = 4\ m [tex]
Encontrando a largura (BC) do telhado, utilizando o teorema de Pitágoras.
[tex] (BC)^{2} = b^{2} + h^{2} [tex]
[tex] (BC)^{2} = 10^{2} + 4^{2} [tex]
[tex] (BC)^{2} = 116 [tex]
[tex] (BC) = \sqrt{116} [tex]
Como o telhado é quadrado. Logo, AB = d = BC = [tex]\sqrt{116}[tex].
Por último a quantidade de telhas é:
[tex] N\ =\ d^{2}\ \cdot\ 10,5\ = (\sqrt{116})^{2}\ \cdot\ 10,5 = 116\ \cdot\ 10,5 = 1\ 218 [tex]
Logo, serão necessários dois milheiros de telhas.
(ENEM 2018 - 2ª Aplicação).
Dois amigos abriram um restaurante. No primeiro ano, o custo total com as despesas do restaurante chegou a 250 mil reais. A receita neste ano foi de 325 mil reais, obtendo assim um lucro de 75 mil reais (diferença entre a receita e o custo total). A tabela representa o custo total e a receita nos cinco primeiros anos.
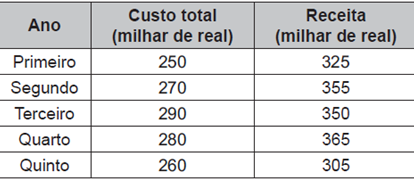
De acordo com a tabela, a média anual do lucro, em milhar de real, ao longo dos cinco anos é
Encontrando o lucro de cada ano:
1° ano: 325 - 250 = 75
2° ano: 355 - 270 = 85
3° ano: 350 - 290 = 60
4° ano: 365 - 280 = 85
5° ano: 305 - 260 = 45
Agora, calculando a média:
[tex] Média = \frac{75 + 85 + 60 + 85 + 45 }{5} = \frac{350}{5} = 70 [tex]
(ENEM 2018 - 2ª Aplicação).
A água comercializada em garrafões pode ser classificada como muito ácida, ácida, neutra, alcalina ou muito alcalina, dependendo de seu pH, dado pela expressão
[tex] pH = log_{10}\frac{1}{H} [tex]
com que H é a concentração de íons de hidrogênio, em mol por decímetro cúbico. A classificação da água de acordo com seu pH é mostrada no quadro.

Para o cálculo da concentração H, uma distribuidora mede dois parâmetros A e B, em cada fonte, e adota H como sendo o quociente de A por B. Em análise realizada em uma fonte, obteve [tex] A = 10^{-7}[tex] e a água dessa fonte foi classificada como neutra.
O parâmetro B, então, encontrava-se no intervalo
Como a água neutra tem pH no intervalo 6 ≤ pH < 7,5 e parâmetro [tex] A = 10^{-7}[tex]. Então,
Parâmetro B para pH = 6.
[tex] H = \frac{A}{B} \Longrightarrow B = \frac{A}{H} = \frac{10^{-7}}{10^{-6}} = 10^{-1} [tex]
Parâmetro B para pH = 7,5.
[tex] H = \frac{A}{B} \Longrightarrow B = \frac{A}{H} = \frac{10^{-7}}{10^{-7,5}} = 10^{0,5} [tex]
Logo, o parâmetro está o intervalo [tex] [10^{-1},\ 10^{\frac{1}{2}})[tex].
(ENEM 2018 - 2ª Aplicação).
Alguns modelos de rádios automotivos estão protegidos por um código de segurança. Para ativar o sistema de áudio, deve-se digitar o código secreto composto por quatro algarismos. No primeiro caso de erro na digitação, a pessoa deve esperar 60 segundos para digitar o código novamente. O tempo de espera duplica, em relação ao tempo de espera anterior, a cada digitação errada. Uma pessoa conseguiu ativar o rádio somente na quarta tentativa, sendo de 30 segundos o tempo gasto para digitação do código secreto a cada tentativa. Nos casos da digitação incorreta, ela iniciou a nova tentativa imediatamente após a liberação do sistema de espera.
O tempo total, em segundo, gasto por essa pessoa para ativar o rádio foi igual a
Como o código de segurança tem 4 algarismos e a pessoa só conseguiu ativar o rádio somente na 4ª tentativa. Logo,
── ── ── ──
1ª tentativa: 60s + 30s de espera = 90s
2ª tentativa: 120s + 30s de espera = 150s
3ª tentativa: 240s + 30s de espera = 270s
4ª tentativa: 30s de espera + código correto.
Portanto, o tempo total é:
90 + 150 + 270 + 30 = 540 s
(ENEM 2018 - 2ª Aplicação).
Uma fábrica comercializa chocolates em uma caixa de madeira, como na figura.

A caixa de madeira tem a forma de um paralelepípedo reto-retângulo cujas dimensões externas, em centímetros, estão indicadas na figura. Sabe-se também que a espessura da madeira, em todas as suas faces, é de 0,5 cm.
Qual é o volume de madeira utilizado, em centímetro cúbico, na construção de uma caixa de madeira como a descrita para embalar os chocolates?
Cálculo do volume de madeira utilizado:
Volume(caixa) = Dimensão(externa) – Dimensão(interna)
V(caixa) = (C × L × H) – (c × l × h)
V(caixa) = (20 × 20 × 8) – (19 × 19 × 7)
V(caixa) = 3 200 – 2 527
V(caixa) = 673 cm³
(ENEM 2018 - 2ª Aplicação).
A quantidade x de peças, em milhar, produzidas e o faturamento y, em milhar de real, de uma empresa estão representados nos gráficos, ambos em função do número t de horas trabalhadas por seus funcionários.

O número de peças que devem ser produzidas para se obter um faturamento de R$ 10 000,00 é
Função quantidade de peças:
[tex] f(t) = \frac{(Δy)t}{(Δx)} + b = \frac{(20-0)t}{1-0}+ 0 = 20t [tex]
Função faturamento:
[tex] g(t) = \frac{(Δy)t}{(Δx)} + b = \frac{(4-0)t}{1-0}+ 0 = 4t [tex]
Encontrando a quantidade peças para ter um faturamento de R$ 10 000,00.
[tex] g(t) = 4t [tex]
[tex] 10 = 4t [tex]
[tex] t = 2,5\ horas [tex]
Logo,
[tex] f(t) = 20t = 20\ \cdot\ 2,5 = 50 [tex]
Portanto, serão produzidas 50 000 peças
(ENEM 2018 - 2ª Aplicação).
Uma pessoa tem massa corporal de 167 kg. Sob orientação de um nutricionista, submeteu-se a um regime alimentar, em que se projeta que a perda de quilos mensais seja inferior a 5 kg. Após iniciar o regime, observou-se, nos três primeiros meses, uma perda de 4 kg por mês, e nos quatro meses seguintes, uma perda mensal de 3 kg. Daí em diante, segundo as recomendações do nutricionista, deveria haver uma perda mensal fixa em cada um dos meses subsequentes, objetivando alcançar a massa corporal de 71 kg ao final do regime.
Segundo as projeções e recomendações do nutricionista, para alcançar seu objetivo, a duração mínima, em mês, que essa pessoa deverá manter o seu regime será de
Seguindo as recomendações do nutricionista, temos:
Nos 3 primeiros meses: 3 × 4kg = 12 kg
Nos 4 meses seguintes: 4 × 3kg = 12 kg
Totalizando 12 + 12 = 24 kg
Tendo que perder ainda:
167 – 71 = 72 kg
Como a perda é fixa e menor que 5kg nos meses subsequentes, logo:
[tex] \frac{72}{5} =\ 14,4\ meses [tex]
Sendo assim, a duração mínima, em mês, que essa pessoa deverá manter o seu regime será de:
[tex] 14,4 \ +\ 7\ = 21,4\ meses\ \cong\ 22\ meses [tex]
(ENEM 2018 - 2ª Aplicação).
Em 2012, o PNUD Brasil, o Ipea e a Fundação João Pinheiro assumiram o desafio de adaptar a metodologia do Índice de Desenvolvimento Humano (IDH) global para calcular o Índice de Desenvolvimento Humano Municipal (IDHM) dos 5 565 municípios brasileiros com base nos dados do Censo Demográfico de 2010. Também se recalculou o IDHM, pela metodologia adotada, para os anos de 1990 e 2000, para permitir a comparabilidade temporal e espacial entre os municípios.
No quadro são apresentados os dados de cinco cidades brasileiras.

Disponível em: http://atlasbrasil.org.br. Acesso em: 26 abr. (adaptado).
Uma ONG decide fazer um trabalho de acompanhamento com a cidade que teve a menor média aritmética dos IDHM das três últimas décadas dentre as cinco cidades analisadas.
Com base nos dados fornecidos, qual foi o município escolhido pela ONG?
Calculando a média aritmética de cada município.
São Caetano do Sul: [tex] \overline{X} = \frac{0,77+0,77+0,92}{3} = \frac{2,46}{3} = 0,82 [tex]
Águas de São Pedro: [tex] \overline{X} = \frac{0,67 + 0,76 + 0,85}{3} = \frac{2,28}{3} = 0,76 [tex]
Florianópolis: [tex] \overline{X} = \frac{0,65 + 0,80+ 0,80}{3} = \frac{2,25}{3} = 0,75 [tex]
Balneário Camboriú: [tex] \overline{X} = \frac{0,79 + 0,79 + 0,79}{3} = \frac{2,37}{3} = 0,79 [tex]
Vitória: [tex] \overline{X} = \frac{0,73 + 0,78 + 0,77}{3} = \frac{2,28}{3} = 0,76 [tex]
Portanto, o município a ser escolhido é Florianópolis.
(ENEM 2018 - 2ª Aplicação).
No final de uma matéria sobre sorte e azar publicada em uma revista, o leitor tem a opção de realizar um teste no qual ele deve responder a dez perguntas sobre cinco temas, sendo cinco sobre sorte e cinco sobre azar. Para cada pergunta, o leitor marca apenas uma alternativa dentre as seis opções de respostas, sendo que a alternativa escolhida está associada a uma nota entre os valores 1, 3, 5, 7, 8 e 9.
Um leitor respondeu ao teste, obtendo as notas de sorte e de azar para as perguntas e representou-as no Quadro 1.

O resultado do teste x é calculado como sendo a diferença entre as médias aritméticas das notas de sorte e de azar, nessa ordem. A classificação desse resultado é dada de acordo com o Quadro 2.

SANTI,A.; KIST, C. Sorte: manual de instruções. Superinteressante. ago. 2012 (adaptado).
De acordo com os dados apresentados, a classificação do resultado do teste desse leitor é
Calculando diferença entre as médias aritméticas das notas de sorte e de azar, nessa ordem
[tex] \overline{X} = \frac{(1-8)+(3-5)+(9-5)+(7-5)+(7-9)}{5} [tex]
[tex] = \frac{-7 -2 +4 + 2 - 2 }{5} = \frac{-5}{5} = -1 [tex]
Logo, você está na média.
(ENEM 2018 - 2ª Aplicação).
Uma empresa especializada em embalagem de papelão recebeu uma encomenda para fabricar caixas para um determinado modelo de televisor, como o da figura.

A embalagem deve deixar uma folga de 5 cm em cada uma das dimensões. Esta folga será utilizada para proteger a televisão com isopor. O papelão utilizado na confecção das caixas possui uma espessura de 0,5 cm.
A empresa possui 5 protótipos de caixa de papelão, na forma de um paralelepípedo reto-retângulo, cujas medidas externas: comprimento, altura e largura, em centímetro, são respectivamente iguais a:
Caixa 1: 68,00 × 50,0 × 18,5
Caixa 2: 68,5 × 50,5 × 19,0
Caixa 3: 72,5 × 54,5 × 23,0
Caixa 4: 73,0 × 55,0 × 23,5
Caixa 5: 73,5 × 55,5 × 24,0
O modelo de caixa de papelão que atende exatamente as medidas das dimensões especificadas é a
Atendendo as especificações da caixa devemos ter:
Comprimento: 5cm + 67,5cm + 0,5 + 0,5 = 73,5 cm
Altura: 5cm + 49,5cm + 0,5 + 0,5 = 55,5 cm
Largura: 5cm + 18cm + 0,5 + 0,5 = 24 cm
Portanto, a caixa que satisfaz a exigências é a caixa 5.
(ENEM 2018 - 2ª Aplicação).
As Artes Marciais Mistas, tradução do inglês: MMA – mixed martial arts, são realizadas num octógono regular. De acordo com a figura, em certo momento os dois lutadores estão respectivamente nas posições G e F, e o juiz está na posição I. O triângulo IGH é equilátero e GÎF é o ângulo formado pelas semirretas com origem na posição do juiz, respectivamente passando pelas posições de cada um dos lutadores.

A medida do ângulo GÎF é

Calculo do ângulo G (octógono regular):
[tex] \hat{G} = \frac{180°\ \cdot\ 6}{8} = \frac{1080°}{8} = 135°[tex]
Logo, o ângulo [tex] I\hat{G}F = 135° - 60° = 75° [tex]
Como o triângulo ΔFGI é isósceles. Logo,
75° + α + α = 180°
2α = 180° – 75°
2α = 105°
α = 52,5°
(ENEM 2018 - 2ª Aplicação).
O presidente de uma empresa, com o objetivo de renovar sua frota de automóveis, solicitou uma pesquisa medindo o consumo de combustível de 5 modelos de carro que usam o mesmo tipo de combustível. O resultado foi:
• Carro I: deslocamento de 195 km consumindo 20 litros de combustível.
• Carro II: deslocamento de 96 km consumindo 12 litros de combustível.
• Carro III: deslocamento de 145 km consumindo 16 litros de combustível.
• Carro IV: deslocamento de 225 km consumindo 24 litros de combustível.
• Carro V: deslocamento de 65 km consumindo 8 litros de combustível.
Para renovar a frota com o modelo mais econômico, em relação à razão quilômetro rodado por litro, devem ser comprados carros do modelo
Encontrando a razão quilômetro rodado por litro para cada carro:
Carro I: [tex] Razão = \frac{195}{20} = 9,75\ km/L [tex]
Carro II: [tex] Razão = \frac{96}{12} = 8\ km/L [tex]
Carro III: [tex] Razão = \frac{145}{16} = 9,06\ km/L [tex]
Carro IV: [tex] Razão = \frac{225}{24} = 9,375\ km/L [tex]
Carro V: [tex] Razão = \frac{65}{8} = 8,125\ km/L [tex]
Logo, o carro mais econômico é o carro que percorre maior distância com 1 litro de combustível. Portanto, deve-se escolher o carro I.
(ENEM 2018 - 2ª Aplicação).
Para garantir segurança ao dirigir, alguns motoristas instalam dispositivos em seus carros que alertam quando uma certa velocidade máxima [tex](V_{máx})[tex], pré-programada pelo usuário de acordo com a velocidade máxima da via de tráfego, é ultrapassada. O gráfico exibido pelo dispositivo no painel do carro após o final de uma viagem fornece a velocidade (km/h) do carro em função do tempo (h).

De acordo com o gráfico, quantas vezes o dispositivo alertou o motorista no percurso da viagem?

Logo, o dispositivo alertou o motorista no percurso da viagem 2 vezes.
(ENEM 2018 - 2ª Aplicação).
Um rapaz possui um carro usado e deseja utilizá-lo como parte do pagamento na compra de um carro novo. Ele sabe que, mesmo assim, terá que financiar parte do valor da compra.
Depois de escolher o modelo desejado, o rapaz faz uma pesquisa sobre as condições de compra em três lojas diferentes. Em cada uma, é informado sobre o valor que a loja pagaria por seu carro usado, no caso de a compra ser feita na própria loja. Nas três lojas são cobrados juros simples sobre o valor a ser financiado, e a duração do financiamento é de um ano. O rapaz escolherá a loja em que o total , em real, a ser desembolsado será menor.
O quadro resume o resultado da pesquisa.
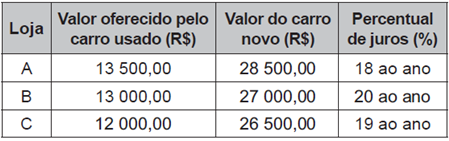
A quantia a ser desembolsada pelo rapaz, em real, será
Loja A: 28 500 – 13 500 = R$ 15 000,00 (valor a ser financiado)
[tex] M = C(1 +it) = 15\ 000(1 + 0,18\ \cdot\ 1) [tex]
[tex] = 15\ 000\ \cdot 1,18 = 17\ 700,00 [tex]
Loja B: 27 000 – 13 000 = R$ 14 000,00 (valor a ser financiado)
[tex] M = C(1 +it) = 14\ 000(1 + 0,2\ \cdot\ 1) [tex]
[tex] = 14\ 000\ \cdot 1,2 = 16\ 800,00 [tex]
Loja C: 26 500 – 12 000 = R$ 14 500,00 (valor a ser financiado)
[tex] M = C(1 +it) = 14\ 500(1 + 0,19\ \cdot\ 1) [tex]
[tex] = 14\ 500\ \cdot 1,19 = 17\ 255,00 [tex]
Logo, a quantia a ser desembolsada pelo rapaz, em real, será de R$ 16 800,00.
(ENEM 2018 - 2ª Aplicação).
Um comerciante abrirá um supermercado, no mês de outubro, e precisa distribuir 5 produtos de limpeza em uma gôndola de cinco prateleiras que estão dispostas uma acima da outra (um tipo de produto por prateleira). Ele sabe que a terceira prateleira oferece uma melhor visibilidade dos produtos aos clientes.
Ele fez uma pesquisa sobre o número de vendas desses produtos, nos meses de agosto e setembro, em uma loja da concorrência (mostrada a seguir), e pretende incrementar suas vendas, em relação a seu concorrente, colocando na terceira prateleira de seu supermercado o produto que teve o maior índice de aumento nas vendas no mês de setembro em relação ao mês de agosto, na loja concorrente.

O comerciante deve colocar na terceira prateleira o produto número
Calculando o índice de aumento de cada produto:
Produto I: [tex] i = \frac{450 }{400} = 1,125 [tex]
Produto II: [tex] i = \frac{295}{210} = 1,404 \cdots [tex]
Produto III: [tex] i = \frac{220}{200} = 1,1 [tex]
Produto IV: [tex] i = \frac{390}{300} = 1,3 [tex]
Produto V: [tex] i = \frac{240}{180} = 1,33\ \cdots [tex]
Logo, o produto que teve o maior índice de aumento nas vendas no mês de setembro em relação ao mês de agosto foi produto II.
(ENEM 2018 - 2ª Aplicação).
A figura a seguir representa parte da planta de um loteamento, em que foi usada a escala 1 : 1 000. No centro da planta uma área circular, com diâmetro de 8 cm, foi destinada para a construção de uma praça.

O diâmetro real dessa praça, em metro, é:
Como a escala é de 1 : 1000. Logo,
1 cm ------ 1000 cm
8 cm ------ x cm
x = 8 000 cm = 80 m
(ENEM 2018 - 2ª Aplicação).
O gerente de uma empresa sabe que 70% de seus funcionários são do sexo masculino e foi informado de que a porcentagem de empregados fumantes nessa empresa é de 5% dos homens e de 5% das mulheres. Selecionando, ao acaso, a ficha de cadastro de um dos funcionários, verificou tratar-se de um fumante.
Qual a probabilidade de esse funcionário ser do sexo feminino?
Pelas informações do enunciado, temos:
masculino: 70% e feminino = 30%
Fumantes: masculino = 5% e feminino = 5%
Logo, a probabilidade é
[tex]P = \frac{30 \%\ \cdot\ 5 \%}{5 \%} = \frac{150 \%}{5 \%} = 30 \%[tex]
(ENEM 2018 - 2ª Aplicação).
O quadro apresenta os dados da pescaria de uma espécie de peixe realizada ao final de um dia de pesca, em lagos diferentes.

Considere que a medida do esforço de pesca (E) seja dada pela função [tex] E = 2 \cdot\ 10^{–7} \cdot\ B \cdot\ H[tex]. A captura (quantidade pescada C) e a população de peixes P(L) dessa espécie no lago L, no início desse dia de pescaria, relacionam-se pela fórmula [tex]C = E \cdot\ P(L)[tex].
Em qual lago a população de peixes dessa espécie era maior no início do dia?
Dados:
E = esforço de pesca
C = quantidade de pescado
P(L) = população de peixes no início do dia de pescaria
L = lago
Calculando a quantidade de peixes em cada lago:
[tex] C = E\ \cdot\ P(L) \Longrightarrow C = 2\ \cdot\ 10^{-7}\ \cdot\ B\ \cdot\ H\ \cdot\ P(L) [tex]
[tex]\Longrightarrow P(L) = \frac{C}{2\ \cdot\ 10^{-7}\ \cdot\ B\ \cdot\ H } [tex]
Logo,
Lago I: [tex] P(L) = \frac{250}{2\ \cdot\ 10^{-7}\ \cdot\ 5\ \cdot\ 5} = \frac{250}{50\ \cdot\ 10^{-7}} = 5\ \cdot\ 10^{7}\ peixes [tex]
Lago II: [tex] P(L) = \frac{300}{2\ \cdot\ 10^{-7}\ \cdot\ 6\ \cdot\ 10} = \frac{300}{120\ \cdot\ 10^{-7}} = 2,5\ \cdot\ 10^{7}\ peixes [tex]
Lago III: [tex] P(L) = \frac{180}{2\ \cdot\ 10^{-7}\ \cdot\ 4\ \cdot\ 5} = \frac{180}{120\ \cdot\ 10^{-7}} = 1,5\ \cdot\ 10^{7}\ peixes [tex]
Lago IV: [tex] P(L) = \frac{215}{2\ \cdot\ 10^{-7}\ \cdot\ 3\ \cdot\ 7} = \frac{215}{42\ \cdot\ 10^{-7}} = 5,1\ \cdot\ 10^{7}\ peixes [tex]
Lago V: [tex] P(L) = \frac{220}{2\ \cdot\ 10^{-7}\ \cdot\ 3\ \cdot\ 10} = \frac{220}{60\ \cdot\ 10^{-7}} = 3,6\ \cdot\ 10^{7}\ peixes [tex]
Portanto, o Lago IV tem maior quantidade peixes no início do dia.
(ENEM 2018 - 2ª Aplicação).
Em uma corrida de dez voltas disputada por dois carros antigos, A e B, o carro A completou as dez voltas antes que o carro B completasse a oitava volta. Sabe-se que durante toda a corrida os dois carros mantiveram velocidades constantes iguais a 18 m/s e 14 m/s. Sabe-se também que o carro B gastaria 288 segundos para completar oito voltas.
A distância, em metro, que o carro B percorreu do início da corrida até o momento em que o carro A completou a décima volta foi mais próxima de
Dados:
• [tex]V_{A}\ =\ 18 m/s [tex] (carro mais rápido)
• [tex]V_{B}\ =\ 14 m/s [tex] (carro mais lento)
• Carro B gasta 288 para completar 8 voltas
Calcular a distância percorrida por 8 voltas do carro B:
[tex] V_{B} = \frac{D}{∆t} \Longrightarrow D = 14\ \cdot\ 288 = 14\ 288\ m [tex]
Agora, encontrar a distância percorrida por 1 volta do carro B:
[tex] D = \frac{14\ 288}{8} = 504\ m [tex]
Em seguida, calcular a distância do carro A (10 voltas):
[tex] D =10\ \cdot\ 504 = 5\ 040\ m [tex]
O próximo passo encontrar o tempo necessário que carro A gastou para completar 10 voltas.
[tex] V_{A} = \frac{D}{∆t} \Longrightarrow ∆t = \frac{5040}{18} = 280\ s [tex]
Por último, encontrar a distância, em metro, que o carro B percorreu do início da corrida até o momento em que o carro A completou a 10ª volta é:
[tex] V_{B} = \frac{∆S}{∆t} \Longrightarrow 14 = \frac{∆S}{280} [tex]
[tex] \Longrightarrow ∆S = 14\ \cdot\ 280 = 3\ 920\ m [tex]
(ENEM 2018 - 2ª Aplicação).
Visando atingir metas econômicas previamente estabelecidas, é comum no final do mês algumas lojas colocarem certos produtos em promoção. Uma determinada loja de departamentos colocou em oferta os seguintes produtos: televisão, sofá e estante. Na compra da televisão mais o sofá, o cliente pagaria R$ 3 800,00. Se ele levasse o sofá mais a estante, pagaria R$ 3 400,00. A televisão mais a estante sairiam por R$ 4 200,00. Um cliente resolveu levar duas televisões e um sofá que estavam na promoção, conseguindo ainda mais 5% de desconto pelo pagamento à vista.
O valor total, em real, pago pelo cliente foi de
Equacionando o problema:
Televisão = T
sofá = S
estante = E
[tex] \begin{cases} T\ +\ S\ = 3\ 800 (I) \\ S\ +\ E\ = 3\ 400 (II) \\ T\ +\ E\ = 4\ 200 (III) \end{cases} [tex]
Subtraindo as equações (I) – (II).
T + S – S – E = 3 800 – 3 400
T – E = 400 (IV)
Somando as equações (III) e (IV):
T – E + T + E = 400 + 4 200
2T = 4 600
T = 2 300
Também, encontrar o valor do Sofá (S):
T + S = 3 800
2 300 – S = 3 800
S = 3 800 – 2 300
S = 1 500
Como o cliente levou duas televisões e um sofá que estavam na promoção, conseguindo ainda mais 5% de desconto pelo pagamento à vista. Logo,
Valor = (2T + S) × 95%
Valor = (2 × 2 300 + 1 500) × 0,95
Valor = (4 600 + 1 500) × 0,95
Valor = 6 100 × 0,95
Valor = R$ 5 795,00
(ENEM 2018 - 2ª Aplicação).
Uma senhora acaba de fazer uma ultrassonografia e descobre que está grávida de quadrigêmeos.
Qual é a probabilidade de nascerem dois meninos e duas meninas?
A probabilidade de ser mulher de cada filho é:
[tex]\frac{1}{2}\ \cdot\ \frac{1}{2}\ \cdot\ \frac{1}{2}\ \cdot\ \frac{1}{2}\ = \frac{1}{16}[tex]
Mas devemos considerar as 6 possibilidades:
HHMM - HMHM - HMMH - MHMH - MMHH - MHHM
Com isso podemos concluir:
[tex] P = 6\ \cdot\ \frac{1}{16}\ = \frac{6}{16}\ = \frac{3}{8} [tex]
(ENEM 2018 - 2ª Aplicação).
Em um jogo de tabuleiro, a pontuação é marcada com fichas coloridas. Cada ficha vermelha vale um ponto. Três fichas vermelhas podem ser trocadas por uma azul, três fichas azuis podem ser trocadas por uma branca, e três fichas brancas podem ser trocadas por uma verde. Ao final do jogo, os jogadores A, B e C terminaram, cada um, com as quantidades de fichas, conforme a tabela seguinte:

De acordo com essa tabela, as classificações em primeiro, segundo e terceiro lugares ficaram, respectivamente, para os jogadores
Pelas informações, obtemos as relações:
•Vermelha = 1 ponto
• Azul = 3 × vermelho = 3 × 1 = 3 pontos
• Branca = 3 × azul = 3 × 3 = 9 pontos
• Verde = 3 × branca = 3 × 9 = 27 pontos
Logo,
Jogador A = 3 Verde + 1 branca + 1 azul + 4 vermelhas = 3 × 27 + 1 × 9 + 1 × 3 + 4 × 1 = 81 + 9 +3 + 4 = 97
Jogador B = 2 Verde + 4 branca + 0 azul + 9 vermelhas = 2 × 27 + 4 × 9 + 0 × 3 + 9 × 1 = 54 + 36 + 9 = 99
Jogador C = 1 Verde + 5 branca + 8 azul + 2 vermelhas = 1 × 27 + 5 × 9 + 8 × 3 + 2 × 1 = 27 + 45 + 24 + 2 = 98
Portanto, o 1° é o jogador B, 2° jogador C e 3° jogador A.
(ENEM 2018 - 2ª Aplicação).
Em março de 2011, um terremoto de 9,0 graus de magnitude na escala Richter atingiu o Japão matando milhares de pessoas e causando grande destruição. Em janeiro daquele ano, um terremoto de 7,0 graus na escala Richter atingiu a cidade de Santiago Del Estero, na Argentino. A magnitude de um terremoto, medida pela escala Richter, é [tex] R = log(\frac{A}{A_{0}})[tex], em que A é a amplitude do movimento vertical do solo, informado em um sismógrafo, A0 é uma amplitude de referência e log representa o logaritmo na base 10.
Disponível em: http://earthquake.usgs.gov.
A razão entre as amplitudes dos movimentos verticais dos terremotos do Japão e da Argentina é
Dados:
A = amplitude do movimento vertical do solo
[tex]A_{0}[tex] = amplitude de referência
Isolando a amplitude do movimento vertical do solo (A):
[tex] R = log(\frac{A}{A_{0}}) \Longrightarrow 10^{R} = \frac{A}{A_{0}} [tex]
[tex] \Longrightarrow A = A_{0}\ \cdot\ 10^{R} [tex]
Agora, calculando a razão:
[tex] Razão: \frac{A_{(Japão)}}{A_{(Argentina)}} = \frac{{A_{0}\ \cdot\ 10^{9}}}{{A_{0}\ \cdot\ 10^{7}}} = 10^{2} = 100 [tex]
(ENEM 2018 - 2ª Aplicação).
A figura mostra uma anticlepsidra, que é um sólido geométrico obtido ao se retirar dois cones opostos pelos vértices de um cilindro equilátero, cujas bases coincidam com as bases desse cilindro. A anticlepsidra pode ser considerada, também, como o sólido resultante da rotação de uma figura plana em torno de um eixo.

Disponível em: www.klickeducacao.com.br. Acesso em: 12 dez. 2012 (adaptado).
A figura plana cuja rotação em torno do eixo indicado gera uma anticlepsidra como a da figura acima é

(ENEM 2018 - 2ª Aplicação).
Um projétil é lançado por um canhão e atinge o solo a uma distância de 150 metros do ponto de partida. Ele percorre uma trajetória parabólica, e a altura máxima que atinge em relação ao solo é de 25 metros.

Admita um sistema de coordenadas xy em que no eixo vertical y está representada a altura e no eixo horizontal x está representada a distância, ambas em metro. Considere que o canhão está no ponto (150; 0) e que o projétil atinge o solo no ponto (0; 0) do plano xy.
A equação da parábola que representa a trajetória descrita pelo projétil é

Do sistema cartesiano obtemos os pontos: (0, 0), (75, 25) e (150, 0).
A função quadrática é do tipo [tex] y = ax² + bx + c [tex].
• Substituindo o ponto (0, 0).
[tex] y = ax² + bx + c [tex]
[tex] 0 = a\ \cdot 0² + b\ \cdot 0 + c [tex]
[tex] c = 0 [tex]
• Agora, substituindo o ponto (75, 25).
[tex] 25 = (75)^{2}a + 75b [tex] (: 75)
[tex] \frac{25}{75} = \frac{75^{2}a}{75}+ \frac{75b}{75} [tex]
[tex] \frac{1}{3} = 75a + b [tex] (I)
• Também, substituindo para o ponto (150, 0).
[tex] 0 = 150^{2}a + 150b+0 [tex] (: 150)
[tex] \frac{0}{150} = \frac{150^{2}}{150} + \frac{150b}{150} [tex]
[tex] 0 = 150a + b [tex] (II)
Agora, resolvendo o sistema das equações (I) e (II).
[tex] \begin{cases} \frac{1}{3} = 75a + b \\ 0 = 150a + b \end{cases} [tex]
[tex] \begin{cases} \frac{1}{3} = 75a + b \\ -150a = b \end{cases} [tex]
Logo,
[tex] \frac{1}{3} = 75a - 150a [tex]
[tex] \frac{1}{3} = - 75a [tex]
[tex] a = - \frac{1}{225} [tex]
e
[tex] 0 = 150\ \cdot \frac{-1}{225} + b [tex]
[tex] 0 = - \frac{150}{225}+ b [tex]
[tex] b = \frac{2}{3} [tex]
Logo, a equação é:
[tex] y = - \frac{1}{225}x^{2}\ +\ \frac{2}{3}x\ +\ 0 [tex]
[tex] \frac{225y\ =\ -x^{2}\ +\ 150x}{225} [tex]
[tex] 225y\ =\ -x^{2}\ +\ 150x [tex]
(ENEM 2018 - 2ª Aplicação).
Um brinquedo chamado pula-pula, quando visto de cima, consiste de uma cama elástica com contorno em formato de um hexágono regular.

Se a área do círculo inscrito no hexágono é 3π metros quadrados, então a área do hexágono, em metro quadrado, é
Cálculo do raio do círculo:
[tex] A_{(círculo)} = πR^{2} [tex]
[tex] 3π = πR^{2} [tex]
[tex] 3 = R^{2} [tex]
Calcular o Lado (L) do hexágono utilizando o teorema de Pitágoras:
[tex]OB^{2} = R^{2} + (\frac{L}{2})^{2} [tex]
[tex] L^{2} = 3 + (\frac{L}{2})^{2} [tex]
[tex] L^{2} = 3 + \frac{L^{2}}{4} [tex]
[tex] L^{2} - \frac{L^{2}}{4} = 3 [tex]
[tex] \frac{4 L^{2} - L^{2} }{4} = 3[tex]
[tex] 3L^{2} = 12 [tex]
[tex] L^{2} = 4 [tex]
[tex] L = 2 [tex]
Agora, a área do hexágono:
[tex] A_{(hexágono)} = 6\ \cdot \frac{L^{2}\sqrt{3}}{4} [tex]
[tex] A_{(hexágono)} = 6\ \cdot \frac{2^{2}\sqrt{3}}{4} [tex]
[tex] A_{(hexágono)} = 6\ \sqrt{3} [tex]
(ENEM 2018 - 2ª Aplicação).
Em certa página de um livro foi anotada uma senha. Para se descobrir qual é a página, dispõe da informação de que a soma dos quadrados dos três números correspondentes à página da senha, à página anterior e à página posterior é igual a um certo número k que será informado posteriormente.
Denotando por n o número da página da senha, qual é a expressão que relaciona n e k?
Equacionando o problema, temos:
• página anterior: [tex]n – 1[tex]
• página atual: [tex]n[tex]
• página posterior: [tex]n + 1[tex]
[tex](n -1)^{2} + n^{2} + (n + 1)^{2} = k [tex]
[tex] n^{2} - 2n + 1 + n^{2} + n^{2}+ 2n + 1 = k [tex]
[tex] 3n^{2} = k - 2 [tex]
(ENEM 2018 - 2ª Aplicação).
Um automóvel pode ser abastecido com os combustíveis A ou B e tem capacidade para armazenar T litro. O quadro indica os preços e mostra o rendimento desse automóvel, por litro, quando abastecido com esses combustíveis.

O dono desse automóvel estabelece duas estratégias de viagem. Em ambas ele irá abastecer duas vezes. O primeiro abastecimento é feito a partir do tanque vazio e o reabastecimento é feito quando o tanque esvaziar novamente.
1ª estratégia de viagem: abastecer meio tanque com o combustível A e depois abastecer um quarto de tanque com o combustível B.
2ª Estratégia de viagem: abastecer meio tanque com o combustível B e depois abastecer um quarto de tanque com combustível A.
O custo (C) da estratégia que possibilita percorrer a maior distância é
Dados:
T = capacidade do tanque em litros
[tex]P_{A}[tex] = preço do combustível A
[tex]P_{B}[tex] = preço do combustível B
Logo, o custo (C) da estratégia que possibilita percorrer a maior distância é
[tex] C = (\frac{T}{2}) \cdot P_{A} + (\frac{T}{4}) \cdot\ P_{B} [tex]
(ENEM 2018 - 2ª Aplicação).
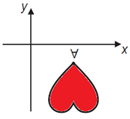
Isometria é uma transformação geométrica que, aplicada a uma figura, mantém as distâncias entre pontos. Duas das transformações isométricas são a reflexão e a rotação. A reflexão ocorre por meio de uma reta chamada eixo. Esse eixo funciona como um espelho, a imagem refletida é o resultado da transformação. A rotação é o "giro" de uma figura ao redor de um ponto chamado centro de rotação. A figura sofreu cinco transformações isométricas, nesse ordem:
1ª) Reflexão no eixo x;
2ª) Rotação de 90 graus no sentido anti-horário, com centro de rotação no ponto A;
3ª) Reflexão no eixo y;
4ª) Rotação de 45 graus no sentido horário, com centro de rotação no ponto A;
5ª) Reflexão no eixo x.
Disponível em: www.pucsp.br. Acesso em: 2 ago. 2012.
Qual a posição final da figura?
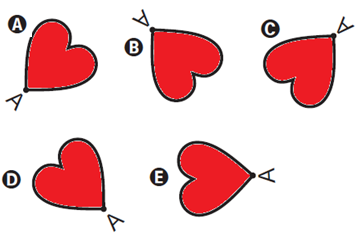
Vamos seguir as etapas:
1ª) Reflexão no eixo x;
2ª) Rotação de 90 graus no sentido anti-horário, com centro de rotação no ponto A;

3ª) Reflexão no eixo y;

4ª) Rotação de 45 graus no sentido horário, com centro de rotação no ponto A;

Por último, 5ª) Reflexão no eixo x.

(ENEM 2018 - 2ª Aplicação).
Um vaso decorativo quebrou e os donos vão encomendar outro para ser pintado com as mesmas características. Eles enviam uma foto do vaso na escala 1 : 5 (em relação ao objeto original) para um artista. Para ver melhor os detalhes do vaso o artista solicita uma cópia impressa da foto com dimensões triplicadas em relação ás dimensões da foto original. Na cópia impressa, o vaso quebrado tem uma altura de 30 centímetros.
Qual é a altura real, em centímetros, do vaso quebrado?
Escala adotada: 1 : 5
cópia impressa da altura: 30 cm (triplicada)
Logo,
1 cm ------- 5 cm (real)
30 cm ----- ---- x cm
x = 150 cm
Como a foto foi triplicado, logo, a altura é [tex] \frac{150}{3} = 50\ cm. [tex]
(ENEM 2018 - 2ª Aplicação).
A resistência elétrica R de um condutor homogêneo é inversamente proporcional à área S de sua seção transversal.

Disponível em: http://efisica.if.usp.br. Acesso em: 2 ago. 2012.
O gráfico que representa a variação da resistência R do condutor em função da área S de sua seção transversal é

Como a resistência elétrica R de um condutor homogêneo é inversamente proporcional à área S de sua seção transversal. Logo,
[tex] R = ρ \frac{L}{A} [tex]
[tex] R = ρ \frac{L}{R^{2}} [tex]
Portanto, aumento raio a resistência diminui. Sendo uma função quadrática. Logo, opção C.
(ENEM 2018 - 2ª Aplicação).
Na música, usam-se sinais gráficos chamados figuras de duração para indicar por quanto tempo se deve emitir determinado som.
A figuras de duração usadas atualmente são: semibreve, mínima, semínima, colcheia, semicolcheia, fusa e semifusa.
Essas figuras não possuem um valor (tempo) fixo. Elas são proporcionais entre si. A duração de tempo de uma semibreve é equivalente à de duas mínimas, a duração de uma mínima é equivalente à de duas semínimas, a duração de uma semínima equivale à de duas colcheias e assim por diante, seguindo a ordem dada.
Considere que a semibreve tem a duração de tempo de uma unidade.

Disponível em: www.portaledumuscalcp2.mus.br. Acesso em: 11 nov. 2013 (adaptado).
A sequência que indica a duração de tempo de uma mínima, de uma semínima, de uma colcheia, de uma semicolcheia, de uma fusa e de uma semifusa é
Como uma semibreve tem a duração de tempo de uma unidade. Logo,
1 mínima → 2 semínimas = [tex] \frac{1}{2}[tex]
1 semínima → 2 colcheia = [tex] \frac{1}{2}\ \cdot \frac{1}{2} = \frac{1}{4} [tex]
1 colcheia → 2 semicolcheia = [tex] \frac{1}{4}\ \cdot \frac{1}{2} = \frac{1}{8} [tex]
1 semicolcheia → 2 fusa = [tex] \frac{1}{8}\ \cdot \frac{1}{2} = \frac{1}{16} [tex]
1 fusa → 2 semifusa = [tex] \frac{1}{16}\ \cdot \frac{1}{2} = \frac{1}{32} [tex]
1 semifusa = [tex] \frac{1}{32}\ \cdot \frac{1}{2} = \frac{1}{64} [tex]
(ENEM 2018 - 2ª Aplicação).
O índice de massa corporal (IMC) de uma pessoa é definido como o quociente entre a massa dessa pessoa, medida em quilograma, e o quadrado da sua altura, medida em metro. Esse índice é usado como parâmetro para verificar se o indivíduo está o não acima do peso ideal para a sua altura. Durante o ano de 2011, uma pessoa foi acompanhada por um nutricionista e passou por um processo de reeducação alimentar. O gráfico indica a variação mensal do IMC dessa pessoa, durante o nutricionista vai analisar as medidas estatísticas referentes à variação do IMC.

De acordo com o gráfico, podemos concluir que a mediana da variação mensal do IMC dessa pessoa é igual a
Ordenando os IMCs:
26,2 - 26,5 - 27,1 - 27,1 - 27,4 - 27,4 - 27,4 - 27,7 - 27,7 - 28,3 - 28,6 - 29,5
Logo,
[tex] Me = \frac{27,4 + 27,4}{2} = 27,4 [tex]
(ENEM 2018 - 2ª Aplicação).
Uma indústria automobilística está testando um novo modelo de carro. Cinquenta litros de combustível são colocados no tanque desse carro, que é dirigido em uma pista de testes até que todo o combustível tenha sido consumido. O segmento de reta no gráfico mostra o resultado desse teste, no qual a quantidade de combustível no tanque é indicada no eixo y (vertical), e a distância percorrida pelo automóvel é indicada no eixo x (horizontal).

A expressão algébrica que relaciona a quantidade de combustível no tanque e a distância percorrida pelo automóvel é
Calculando o coeficiente angular e linear da função. Logo,
• coeficiente angular
[tex] m = \frac{Δy}{Δx} = \frac{50-0}{0-500} = \frac{50}{-500}= -\frac{1}{10} [tex]
• coeficiente linear:
[tex] n = 50 [tex]
Portanto,
[tex] y = mx + n [tex]
[tex] y = (- \frac{1}{10})x\ + 50 [tex]
[tex] y = - \frac{x}{10}x\ + 50 [tex]

Nenhum comentário:
Postar um comentário