(ENEM 2014 - 3ª Aplicação).
Ao elaborar um programa de condicionamento para um atleta, um preparador físico estipula que ele deve correr 1000 metros no primeiro dia e, nos dias seguintes, 200 metros a mais do que correu no dia anterior. O treinador deseja que, ao final dos dias de treinamento, o atleta tenha percorrido, em média, 1700 m por dia.
Esse atleta deve participar desse programa por
Dados:
[tex] a_{1} = 1000m [tex]
[tex] r = 200m [tex]
[tex] S_{n} = 1700 \cdot n [tex]
[tex] a_{n} = ? [tex]
[tex] n = ? [tex]
Calcular o último termo:
[tex] S_{n} = \frac{(a_{1} + a_{n})n}{2} [tex]
[tex] 1700\ n = \frac{(1000 + a_{n})n}{2} [tex]
[tex] \frac{2\ \cdot\ 1700\ n }{n} = 1000 + a_{n} [tex]
[tex] 3400 = 1000 + a_{n} [tex]
[tex] 3400 - 1000 = a_{n} [tex]
[tex] a_{n} = 2400 [tex]
Agora, encontrar o número de dias "n".
[tex] a_{n} = a_{1} + (n - 1)r [tex]
[tex] 2400 = 1000 + (n - 1)\cdot 200 [tex]
[tex] 2400 - 1000 = 200n - 200 [tex]
[tex] 1400 + 200 = 200n [tex]
[tex] 1600 = 200n [tex]
[tex] n = 8\ dias [tex]
(ENEM 2014 - 3ª Aplicação).
Um medidor de velocidade funciona com dois sensores instalados sob o asfalto. Um microprocessador recebe os sinais elétricos emitidos pelos sensores, calculando a velocidade v em função da distãncia fixa entre os sensores e o tempo gasto durante a passagem distância do veículo, assim,

tempo Se a velocidade for maior do que a máxima permitida para a via, um sistema de vídeo é acionado para capturar a imagem do veículo infrator. Dois destes medidores estão instalados em uma avenida, onde a velocidade máxima permitida é de 60 km/h e a distância entre os sensores é de meio metro (0,5 m).
Um motorista dirige um carro, nessa avenida, com o velocímetro descalibrado. Ao passar pelo primeiro medidor ele se lembra da existência dos medidores, reduzindo em 10 km/h a velocidade do seu veículo, e passa pelo segundo medidor. Sabe-se que o microprocessador do primeiro medidor registrou que o veículo passou entre os sensores em 0,024 segundos e, pela legislação vigente, a multa é classificada em:
Média: se a velocidade do veículo é maior do que 60 km/h e menor ou igual a 72 km/h;
Grave: se a velocidade do veículo é maior do que 72 km/h e menor ou igual a 90 km/h;
Gravíssima: se a velocidade do veículo é maior do que 90 km/h.
(Para transformar a velocidade de m/s para km/h multiplica-se por 3,6).
Qual(ais) multa(s) esse infrator recebeu?
Ao passar pelo primeiro medidor, este registrou:
[tex] v = \frac{ΔS}{Δt} = \frac{0,5m}{0,024s} = \frac{500}{24}m/s [tex]
Agora, transformando em km/h, fica:
[tex] \frac{500}{24} \cdot 3,6 = 75\ km/h [tex] (grave)
Como ao passar pelo segundo, como o motorista reduziu sua velocidade em 10 km/h, o respectivo medidor deve ter registrado a velocidade de:
75 – 10 = 65 km/h (Média)
(ENEM 2014 - 3ª Aplicação).
Uma pessoa, durante sua vida, cometeu crimes, sendo, por consequência, condenada a 10 anos de cadeia. Ainda no tribunal, o juiz, interessado na recuperação dessa pessoa, lhe informou acerca da possibilidade que tinha em reduzir sua pena, caso se dispusesse a trabalhar na marcenaria da penitenciária. Informou-a que a cada 3 dias de trabalho, 1 dia seria "perdoado" em sua pena.
Imaginando não haver outras formas de progressão de pena, e considerando que a pessoa trabalhe todos os dias da semana, quanto tempo ela deverá permanecer presa?
Em 10 anos há 10 × 365 dias = 3 650 dias.
Os dias de trabalho correspondem a [tex]\frac{3}{4}[tex] dos 4 dias propostos, igualmente correspondem a [tex]\frac{3}{4}[tex] deste total de 3650 dias. Assim,
[tex] \frac{3}{4} × 3650 \cong [tex] 2737,5 dias.
Portanto, O número de anos é dado por 2737,5 ÷ 365 [tex]\cong [tex] 7,5 anos
(ENEM 2014 - 3ª Aplicação).
A direção de uma escola comprará lapiseiras para distribuir para os seus alunos. Sabe-se que x lapiseiras custam y reais. O número máximo de lapiseiras que a direção da escola conseguirá comprar com z reais é o maior inteiro menor do que, ou igual a
z reais não são, evidentemente, y reais. Por isso o número de lapiseiras que poderá ser comprado não é x. Mas, o número de lapiseiras que se pode comprar é proporcional à quantia de dinheiro em mãos (quanto mais dinheiro, mais lapiseiras)
Regra de três:
x lapiseiras ----- y reais
N lapiseiras ----- z reais
[tex] N = \frac{x\ \cdot\ z}{y} [tex]
(ENEM 2014 - 3ª Aplicação).
Uma pesquisa do Instituto de Pesquisa Econômica (Ipea) investigou qual área faz a economia crescer mais e quais os maiores responsáveis pela diminuição da desigualdade na distribuição de renda.

Considerando apenas as áreas que contribuem para o crescimento econômico mais do que o investimento em exportação, qual delas é a que mais influencia para a maior igualdade?

Analisando o eixo do crescimento, desconsideraremos todos abaixo do investimento em exportação. Dos que restaram (Construção, Saúde e Educação), o setor de Saúde é o que mais proporciona uma distribuição de renda com maior igualdade.
(ENEM 2014 - 3ª Aplicação).
Até o fim do Império, as mulheres eram tolhidas em seu acesso à escola. Já na década de 1930, o número de meninas e meninos nas instituições de ensino fica igual. Hoje, as mulheres são maioria em todos os níveis de ensino — do fundamental à pós-graduação. Veja a tabela a seguir:

Considerando os dados apresentados tem-se que, escolhida ao acaso uma brasileira com mais de 10 anos, a probabilidade de que ela possua oito anos ou mais de estudos é igual a
De 8 a 10 = 17 e 11 ou mais = 33
Agora, encontrando 8 ou mais, ou seja:
17,1 + 33,4 = 50,5%
(ENEM 2014 - 3ª Aplicação).
Um fabricante planeja colocar no mercado duas linhas de cerâmicas para revestimento de pisos. Diversas formas possíveis para as cerâmicas foram apresentadas e decidiu-se que o conjunto P de formas possíveis seria composto apenas por figuras poligonais regulares. Duas formas geométricas que fazem parte de P são
Imagine um ponto de encontro dos vértices de todos os polígonos assentados no piso. Para que não haja sobra, o ângulo interno de um polígono adequado tem que ser um divisor de 360 graus: Assim, ângulo interno de um polígono de n lados: [tex] i = \frac{180(n - 2)}{n} [tex].
Assim,
[tex] i = \frac{180(3 - 2)}{3} = 60° [tex], que é divisor de 360°; triângulo (OK)
[tex] i = \frac{180(5 - 2)}{5} = 108° [tex] , que não é divisor de 360°; pentágono (Não)
[tex] i = \frac{180(6 - 2)}{6} = 120° [tex] , que é divisor de 360°; hexágono (OK)
[tex] i = \frac{180(8 - 2)}{8} = 135° [tex] , que não é divisor de 360°; octógono (Não)
[tex] i = \frac{180(7 - 2)}{7} = 128,6° [tex] , que não é divisor de 360; heptágono (Não)
Logo, as duas formas geométricas são o triângulo e o hexágono.
(ENEM 2014 - 3ª Aplicação).
Ao alugar um carro, o locatário precisa pagar R$ 60,00 por dia, e mais R$ 1,50 por quilômetros rodado. Para facilitar, as locadoras podem fazer uma relação entre o valor a ser pago P, em reais, em função dos quilômetros rodados, representado por x. Qual das expressões abaixo representa o valor pago pelos locatários em função dos quilômetros rodados?
Função afim: parte fixa + parte variável.
Logo,
P = parte fixa + parte variável
P = 60 + 1,50x
(ENEM 2014 - 3ª Aplicação).
Estudo com funcionários que trabalham como caixas de supermercado revelou que metade deles apresentou sinais de infecção urinária. A maioria fica até 5 horas sem beber água e sem urinar. Segundo a pesquisadora Thalita Galindo, é necessário ingerir água diariamente e o ideal de consumo de água diário seria ingerir 35 mililitros de água para cada quilo de peso.
Jornal do Comércio, 22 jan. 2012 (adaptado).
Sabe-se que uma pessoa pesando 80 kg consome 6 galões de 20 litros de água em 60 dias. Para que essa pessoa atinja a ideal ingestão diária de água, a quantidade mínima de litros de água que ela deve acrescentar à sua ingestão diária média, no mesmo período de dias, deve ser de
35 mL ----- 1 kg
x -------- 80 kg
x = 2 800 mL
Assim, 20 × 6 = 120 L = 120 000 mL
[tex] \frac{120 000}{60} = 2 000\ mL [tex]
2800 - 2000 = 800 mL = 0,8 L
(ENEM 2014 - 3ª Aplicação).
A empresa E fornece linhas para telefones celulares da Companhia de Telefonia X a dois de seus funcionários. Os funcionários 1 e 2 usam, em média, 170 minutos e 195 minutos mensais, em ligações, respectivamente.
O plano das linhas desses celulares possui uma franquia de 90 minutos mensais (ou seja, 90 minutos de ligações grátis a cada mês), e custo de R$ 0,20 por minuto adicional, além de um custo fixo de R$ 30,00 mensais.
A companhia X lançou novos planos que podem baratear o custo da empresa E com esses celulares e ofereceu-lhes, com preços mostrados a seguir:

Mas, por contrato, E só pode migrar uma das contas para um novo plano, enquanto a outra precisa continuar no plano em que está.
De modo a ter o menor custo possível com os pagamentos dessas contas de celulares, qual é a melhor atitude a ser tomada pela empresa E em relação às ofertas descritas?
Plano antigo:
P(x) = 90,00 + (0,20x + 30,00)
Plano novo:
Plano Dourado: P(x) = 120,00 + (0,22x + 20,00)
Plano Parceria: P(x) = 110,00 + (0,25x +15,00)
Agora, considerando o valor máximo do tempo de ligação, ou seja, 195 minutos mensais.
Funcionário 1:
Plano Dourado: P(x) = 120,00 + (0,22 × 170 + 20,00)
P(x) = 120,00 + 37,40 + 20,00
P(x) = 177,40
Plano Parceria: P(x) = 110,00 + (0,25 × 170 +15,00)
P(x) = 110,00 + 42,50 + 15,00
P(x) = 167,50
Funcionário 2:
Plano Dourado: P(x) = 120,00 + (0,22 × 195 + 20,00)
P(x) = 120,00 + 42,90 + 20,00
P(x) = 182,90
Funcionário 2:
Plano Parceria: P(x) = 110,00 + (0,25 × 195 +15,00)
P(x) = 110,00 + 48,75 + 15,00
P(x) = 173,75
Logo, fornecer o Plano Parceria para o funcionário 1.
(ENEM 2014 - 3ª Aplicação).
Um pequeno comerciante pretende aplicar R$ 60 000,00 em ações na Bolsa de Valores. O quadro seguinte traz algumas das opções de investimento.

Dentre as opções apresentadas no quadro, a melhor aplicação para esse montante de dinheiro é
Efetuando a diferença entre o retorno e a taxa de administração, temos:
WWWW: 27,5% – 12% = 15,5%
BBBT: 24,7% – 15% = 9,2%
BGT Capital: 29,5% – 13% = 16,5%
JGPF: 25,9% – 14% = 9,4 %
IKPQ: 23,9% – 11% = 12,9%
Logo, deve-se escolher a aplicação BGT Capital.
(ENEM 2014 - 3ª Aplicação).
Uma pessoa precisa comprar creme dental. Ao entrar em um supermercado, encontra uma marca em promoção, conforme o quadro seguinte:

Pensando em economizar seu dinheiro, resolve levar a embalagem de número
Embalagem n° 1: [tex] \frac{3}{2} = 1,5 [tex]
Embalagem n° 2: [tex] \frac{4}{3} = 1,333 ... [tex]
Embalagem n° 3: [tex] \frac{5}{4} = 1,25 [tex]
Embalagem n° 4: [tex] \frac{7}{5} = 1,4 [tex]
Embalagem n° 5: [tex] \frac{10}{7} = 1,42... [tex]
Logo, é melhor a embalagem n° 1.
(ENEM 2014 - 3ª Aplicação).
Cleber precisava ir a uma papelaria. Sabia a localização do ponto de ônibus em que deveria descer.
Quando desceu do ônibus, andou 1/2 de 1 km para o Sul, depois 2 km para o Leste, em seguida 3 mil metros para o Norte e por fim 10/4 de 1 km para Oeste.
Observe a rosa dos ventos a seguir.

Considere uma malha quadriculada formada por quadrados cujos lados medem 500 m.
Se a localização inicial de Cleber é dada pelo ponto A e a localização final é dada pelo ponto B, qual malha representa as localizações inicial e final de Cleber, de acordo com a descrição?


(ENEM 2014 - 3ª Aplicação).
Muitas pessoas, de modo descuidado, armazenam em caixas plásticas restos de alimentos em locais não apropriados, criando condições para o aparecimento de formigas e roedores. Suponha que uma formiga, localizada no vértice J de uma caixa plástica que ficou destampada, avista um torrão de açúcar no vértice P da caixa, conforme ilustra a figura seguinte. Caminhando sobre a superfície da caixa (arestas e lados) ela poderá seguir várias trajetórias até ele:

Observação: Considere que R é o ponto médio da aresta NQ.
Para que o caminho percorrido pela formiga tenha o menor comprimento possível, ela deve seguir o caminho


(ENEM 2014 - 3ª Aplicação).
O governo, num programa de moradia, tem por objetivo construir 1 milhão de habitações, em parceria com estados, municípios e iniciativa privada. Um dos modelos de casa popular proposto por construtoras deve apresentar 45 m² e deve ser colocado piso de cerâmica em toda sua a área interna.
Supondo que serão construídas 100 mil casas desse tipo, desprezando-se as larguras das paredes e portas, o número de peças de cerâmica de dimensões 20 cm × 20 cm utilizadas será
Cálculo da quantidade de cerâmica em 1 casa:
45 m² = 450 000 cm² e (20 × 20) = 400 cm²
Logo,
[tex] \frac{450 000}{400} = 1 125[tex] peças de cerâmica.
Assim, em 100 mil casas temos:
100 000 × 1 125 peças = 112 500 000
(ENEM 2014 - 3ª Aplicação).
O gelo marinho no Ártico está em sua segunda menor extensão já registrada: 5,56 milhões de km2. Essa medida foi feita com o auxílio de satélites no dia 14 de agosto de 2011 e é apenas 220 mil km² maior do que a baixa recorde de 2007.
ANGELO, C. Volume de gelo no Ártico nunca foi tão baixo. Disponível em: www1.folha.uol.com.br.Acesso em: 08 nov. 2011
De acordo com esses dados, a menor extensão territorial do gelo marinho registrada no Ártico em 2007, em metros quadrados, foi
Veja que:
1 km² = 1 000 000 m² = 1 × 10⁶ m²
5,56 milhões de km² = 5,56 × 10⁶ × 10⁶ = 5,56 × 10¹² m²
220 mil de km² = 220 × 10³ × 10⁶ = 220 × 10⁹ m² ou 0,220 ×10¹² m²
Logo,
5,56 × 10¹² m² – 0,22 × 10¹² m² = 5,34 × 10¹² m²
(ENEM 2014 - 3ª Aplicação).
Todos os anos são registrados milhares de acidentes nas rodovias. Um número significativo desses acidentes ocorre no período de carnaval. De acordo com a Polícia Rodoviária Federal (PRF), o número de acidentes registrados no carnaval teve uma redução de 4 312, registrados em 2011, para 3 345 em 2012. O quadro mostra os números registrados de alguns estados brasileiros.

De acordo com o quadro apresentado, o estado que apresentou maior queda percentual no número de acidentes foi
Cálculo da maior queda percentual:
Rio de Janeiro: [tex] \frac{378 - 302}{378} = \frac{76}{378} = 0,2010 ... = 20,1 \% [tex]
Pernambuco: [tex] \frac{178 - 129}{178} = \frac{49}{178} = 0,2752 ... = 27,5 \% [tex]
Pará: [tex] \frac{107 - 78}{107} = \frac{29}{107} = 0,2710 ... = 27,1 \% [tex]
Mato Grosso: ocorreu foi aumento do percentual
Portanto, o estado do Pernambuco ocorreu a maior queda percentual com 27,5%
(ENEM 2014 - 3ª Aplicação).
Em uma cidade turística, três hotéis ofereceram promoções para o mês de abril de 2011 e compararam as taxas de ocupação nesse mês com as de abril de 2010. Os descontos praticados estão descritos a seguir:
• Hotel 1: Foi dado um desconto de 10% nas diárias, elevando a ocupação de 70% em 2010 para 80% em 2011.
• Hotel 2: Foi dado um desconto de 15% nas diárias, elevando a ocupação de 60% em 2010 para 100% em 2011.
• Hotel 3: Foi dado um desconto de 20% nas diárias, elevando a ocupação de 10% em 2010 para 60% em 2011.
• Hotel 4: Foi dado um desconto de 25% nas diárias, elevando a ocupação de 30% em 2010 para 90% em 2011.
• Hotel 5: Foi dado um desconto de 30% nas diárias, elevando a ocupação de 40% em 2010 para 60% em 2011.
Após o término de 2011, foi feita uma avaliação sobre os impactos desses descontos nos valores arrecadados pelos hotéis. O hotel que apresentou a maior diferença na taxa de arrecadação de 2010 para 2011 foi o

(ENEM 2014 - 3ª Aplicação).
Um jogo entre dois jogadores tem as seguintes regras:
• (a ) o primeiro jogador pensa em uma forma geométrica, desenha apenas uma parte da forma e fornece uma dica para que o segundo jogador termine o desenho;
• (b ) se o segundo jogador conseguir concluir o desenho, ganha um ponto; caso contrário, quem ganha um ponto é o primeiro jogador.
Dois amigos, Alberto e Dora, estão jogando o referido jogo. Alberto desenhou a figura a seguir e deu a seguinte dica a Dora: "a forma em que pensei é a planificação de um prisma reto".
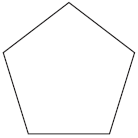
Dora completou o desenho com
Completou com um pentágono e cinco retângulos.

(ENEM 2014 - 3ª Aplicação).
Um estudo feito em cidades brasileiras aponta que apenas 15% dos diabéticos do país fazem bom controle da doença. A pesquisa, que foi feita por meio da análise dos prontuários e questionários respondidos por pacientes entre 2008 e 2010, analisou os dados de 3 580 pessoas de 20 cidades nas cinco regiões do Brasil.
Disponível em: http://noticias.uol.com.br. Acesso em: 14 nov. 2011 (adaptado).
Entre todos que participaram da pesquisa, qual é o número de pessoas que fazem um bom controle do diabetes?
3580 ------ 100%
x ------ 15%
100x = 53700
x = 537 pessoas
(ENEM 2014 - 3ª Aplicação).
A velocidade Mach (M ) de um avião é definida como a razão entre a velocidade do avião e a velocidade do som. Os aviões são classificados em categorias, de acordo com a velocidade que conseguem atingir. As categorias são: subsônica (M < 1,0), transônica ( 1,0 ≤ M < 1,2), supersônica (1,2 M ≤ 5,0) e hipersônica (1,2 ≤ M < 5,0). Considere a velocidade do som igual a 1 200 km/h.
João e Bia fizeram uma viagem de avião, que percorreu 3 600 km em 4 horas.
Bia disse que esse avião era muito rápido e, portanto, supersônico. João convenceu Bia de que ela estava errada, argumentando que, para o avião ser supersônico, o tempo de sua viagem deveria ser reduzido em, no mínimo,
Dados:
[tex] M = \frac{Vo}{Vs} [tex]
M = Mach
Vo = velocidade média relativa do objeto = 3 600km/4h = 900 km/h
Vs = velocidade média do som 1 200 km/h
[tex]M = \frac{900}{1200} = 0,75[tex] avião subsônico
(1,2 ≤ M < 5,0) = supersônico
[tex] M_{min} = \frac{Vo}{Vs} [tex]
[tex] 1,2 = \frac{Vo}{1200} [tex]
[tex] Vo = 1\ 440\ km/h [tex]
1 440 --- 1h
3 600 --- x
[tex] x = \frac{3600}{1440} = 2,5\ h [tex]
Tempo reduzido de 4h para 2,5 h.
Logo, reduziu-se 1,5 h.
(ENEM 2014 - 3ª Aplicação).
Em 2010, o mundo produziu uma quantidade de alimentos adequada para 5,5 bilhões de pessoas. A população mundial era de 6,5 bilhões e 1 bilhão de pessoas passou fome, segundo a FAO. Em 2050, estimativas indicam que a população mundial será de nove bilhões, ou seja, será preciso aumentar bastante a oferta de alimentos nos próximos 40 anos. Considere que a quantidade de alimentos produzidos em 2050 seja 40% superior à de 2010.
Disponível em: http://blogdaterra.com.br. Acesso em: 28 ago. 2011 (adaptado).
De acordo com os dados e estimativas apresentados, a quantidade de pessoas, em bilhões, que passará fome em 2050, será igual a
6,5 bilhões ------- 1 bilhão
9 bilhões ------- x
6,5 x = 9
[tex] x = \frac{9}{6,5} [tex]
x = 1,384 ....
(ENEM 2014 - 3ª Aplicação).
Em uma determinada estrada existem dois telefones instalados no acostamento: um no quilômetro 30 e outro no quilômetro 480. Entre eles serão colocados mais 8 telefones, mantendo-se entre dois telefones consecutivos sempre a mesma distância.
Qual a sequência numérica que corresponde à quilometragem em que os novos telefones serão instalados?
Dados:
[tex] a_{1} = 30 [tex]
[tex] a_{n} = 480 [tex]
n = 2 + 8 = 10
r = ?
[tex] a_{n} = a_{1} + (n - 1) r [tex]
[tex] 480 = 30 + (10 - 1) r [tex]
[tex] 480 - 30 = 9r [tex]
[tex] 450 = 9r [tex]
r = 50
Logo,
30 - 80 - 130 - 180 - 230 - 280 - 330 - 380 - 430
(ENEM 2014 - 3ª Aplicação).
Tanto na natureza, quanto na indústria, existem diversos tipos de fluidos. Fluidos Newtonianos são aqueles que apresentam crescimento linear da tensão cisalhante com relação ao gradiente de velocidade, com coeficiente angular não nulo. Apresentam ainda tensão cisalhante nula com gradiente de velocidade zero. Afigura apresenta a relação da tensão cisalhante com o gradiente de velocidade para diversos tipos de fluidos.

Dentre as curvas da figura, determine qual(is) é(são) de fluido(s) Newtoniano(s).
De acordo a definição de fluidos Newtonianos que apresenta crescimento linear da tensão cisalhante e tensão cisalhante nula com gradiente de velocidade zero é a CURVA C.
(ENEM 2014 - 3ª Aplicação).
Um indivíduo possui uma renda mensal de R$ 1 200,00 e deseja comprar um refrigerador. Na loja que ele decide fazer sua compra, o refrigerador custa R$ 1 800,00. Esse valor deverá ser pago em 12 prestações mensais iguais e sem juros.
Uma forma de representar a quantia da renda mensal do indivíduo que será usada para pagar cada prestação é
Valor de cada prestação:
[tex] \frac{ R \$ 1 800,00}{12} = R \$ 150,00 [tex]
Assim,
[tex] \frac{150}{1200} = [tex] ( dividir por 15)
[tex] = \frac{1}{8} [tex]
(ENEM 2014 - 3ª Aplicação).
O filme A corrente do bem conta a história de um jovem que crê ser possível mudar o mundo a partir da ação voluntária de cada um. A ideia é baseada em três premissas: fazer por alguém algo que este não pode fazer por si mesmo; fazer isso para três pessoas; cada pessoa ajudada deve fazer isso por outras três pessoas. Da mesma forma que temos a "corrente do bem" para 3 pessoas, podemos ter uma corrente do bem para um número qualquer de pessoas. Suponha que uma corrente do bem seja iniciada numa segunda-feira, com X pessoas sendo ajudadas, e que cada uma dessas X pessoas ajudasse outras X pessoas exatamente 24 horas após ter recebido a ação voluntária.
Disponível em: www.webcine.com.br. Acesso em: 18 fev. 2012
Para termos um total de 42 pessoas ajudadas ao término da terça-feira o número X deve ser igual a
Na 2ª feira temos x pessoas e na terça feira é passou para x² pessoas.
Trata-se da soma dos termos de uma PG com n = 2 termos, [tex]a_{1}[tex] = x, q = x.
[tex] S = a_{1} \cdot \frac{q^{n} - 1}{q - 1} [tex]
[tex] 42 = x \cdot \frac{x^{2} - 1}{x - 1} [tex]
[tex] 42 = \frac{x \cdot (x +1)(x - 1)}{x - 1} [tex]
[tex] 42 = x(x - 1) [tex]
[tex] x^{2} + x - 42 = 0 [tex]
Resolvendo a equação do 2° grau, obtemos:
x' = 6 e x" = –7 (não convém).
(ENEM 2014 - 3ª Aplicação).
Desde 2005, o Banco Central não fabrica mais a nota de 1real e, desde então, só produz dinheiro neste valor em moedas. Hoje, há pouco mais de 159 milhões de cédulas de 1 real em circulação no Brasil, contra 1,6 bilhão de moedas do mesmo valor. O Brasil chegou a ter 1 bilhão de cédulas de 1 real em circulação, mas o número só diminui com o tempo. Apesar de ser mais caro produzir uma moeda, a durabilidade do metal é 30 vezes maior que a do papel.Fabricar uma moeda de R$ 1 custa R$ 0,26, enquanto a nota custava R$ 0,17, entretanto, a cédula durava de oito a 11 meses.
Disponível em: http://noticias.r7.com. Acesso em: 26 abr. 2010.
O tempo mínimo de durabilidade da moeda é
Observe que:
8 meses × 30 vezes = 240 meses = 20 anos
(ENEM 2014 - 3ª Aplicação).
Em uma plantação de eucaliptos, um fazendeiro aplicará um fertilizante a cada 40 dias, um inseticida para combater as formigas a cada 32 dias e um pesticida a cada 28 dias. Ele iniciou aplicando os três produtos em um mesmo dia. De acordo com essas informações, depois de quantos dias, após a primeira aplicação, os três produtos serão aplicados novamente no mesmo dia?
Encontrando o mmc, temos:
40, 32, 28 | 2
20, 16, 14 | 2
10, 08, 07 | 2
05, 04, 07 | 2
05, 02, 07 | 2
05, 01, 07 | 5
01, 01, 07 | 7
01, 01, 01
Assim,
mmc = 25 × 5 × 7 = 1 120 dias
(ENEM 2014 - 3ª Aplicação).
A fim de expandir seus investimentos, um banco está avaliando os resultados financeiros de duas seguradoras de veículos de uma cidade.
O seguro de um carro custa, em média, R$ 2 000,00 na seguradora X e R$ 3 000,00 na seguradora Y; já o valor pago pela seguradora a um cliente, vítima de roubo, é de R$ 42 000,00 na seguradora X e de R$ 63 000,00 na seguradora Y.
Pesquisas revelam que, nesta cidade, a probabilidade de um veículo ser roubado é de 1%.
Sabe-se que essas duas seguradoras têm a mesma quantidade de clientes e que o banco optará pela seguradora que possuir o maior lucro médio por veículo.
A seguradora escolhida pelo banco e o lucro médio por veículo nessa escolha serão, respectivamente,
A cada 100 carros que estão numa seguradora, 1 é roubado. Assim:
A cada R$ 200 000,00 recebido, ela paga R$ 42 000,00.
R$ 200 000,00 – R$ 42 000,00 = R$ 158 000,00.
Então por mês, ela lucra R$ 158 000 no total.
O que, dividido pela quantidade de carros (100), temos:
[tex] \frac{158 000}{100} = R \$\ 1\ 580,00[tex] de lucro por carro.
Para cada R$ 300 000,00 recebido, paga-se R$ 63 000,00.
R$ 300 000,00 – R$ 63 000,00 = R$ 237 000,00
Logo, por mês, a seguradora lucra R$ 237\ 000,00 por mês.
O que, dividindo pela quantidade de carros (100), temos:
[tex] \frac{237 000}{100} = R \$\ 2 370,00[tex] de lucro por carro.
Logo, opção B.
(ENEM 2014 - 3ª Aplicação).
Um conjunto residencial será construído em um terreno que está representado no mapa a seguir na escala 1 : 1 000. O terreno está divido em lotes quadrados iguais ao indicado na figura. No local, será construído um centro comunitário, quiosques e praças de lazer e alimentação, de tal forma que a soma total dessas áreas não ultrapasse 2/5 da área total do terreno.

A área total, a ser disponibilizada para a construção do centro comunitário, dos quiosques e das praças de lazer e alimentação, não poderá ultrapassar
Área do terreno: [tex]\frac{2}{5}[tex] ∙ área total = ?
Escala: 1 : 1 000 → 1cm : 10m
1 m² = 10 000 cm²
Agora, utilizando a escala, temos:
10 × (10cm × 10cm) → 10 × (100 m × 100 m) = 100 000 m²
Portanto,
[tex]\frac{2}{5}[tex] ∙ área total = [tex]\frac{2}{5}[tex] ∙ 100\ 000 m²
[tex] = \frac{200\ 000}{5} = 40\ 000[tex] m²
(ENEM 2014 - 3ª Aplicação).
Um paciente inicia um tratamento em que deve ingerir uma dose de um determinado remédio a cada duas horas. Ao ingerir essa dose, a quantidade Q de uma substância no seu organismo aumenta instantaneamente em 2 unidades. Nas próximas duas horas, essa quantidade decresce de maneira linear até atingir a quantidade existente no momento imediatamente anterior à ingestão do remédio. Por descuido, esse paciente tomou a segunda dose do remédio uma hora depois da primeira. A partir daí, não cometeu mais esse tipo de engano, tomando o remédio a cada duas horas. Antes da primeira dose, a quantidade da substância na corrente sanguínea do paciente era de 1 unidade.
O gráfico que melhor representa a quantidade da substância no organismo do paciente nas sete primeiras horas do tratamento é

Opção A.
(ENEM 2014 - 3ª Aplicação).
O número de pessoas que morrem nas ruas e estradas brasileiras nunca foi tão alto. As últimas mudanças na legislação mostraram-se incapazes de frear o aumento dos acidentes. O número de mortes em 2004 foi de 35 100 pessoas e 38 300, em 2008. Admita que o número de mortes, no período de 2004 a 2008, tenha apresentado um crescimento anual constante.
Veja, 2 nov. 2011 (adaptado).
A expressão algébrica que fornece o número de mortes N, no ano x (com 2004 ≤ x ≤ 2008), é dada por
É função afim, pois apresenta um crescimento anual constante. Então, vamos encontrar o coeficiente angular que passa pela reta A(2 004, 35 100) e B(2 008, 38 300):
[tex] m =\frac{ Δy}{Δx} = \frac{38\ 300\ –\ 35 100}{2008\ –\ 2004} [tex]
[tex] = \frac{3200}{4} = 800 [tex]
Sendo assim, a equação da reta para m = 800 e A(2 004, 35 100).
y – yo = m (x – xo)
y – 35 100 = 800 (x – 2004)
y = 800 (x – 2004) + 35 100
(ENEM 2014 - 3ª Aplicação).
O gráfico a seguir mostra a evolução da taxa de desemprego (ou seja, a porcentagem da população economicamente ativa que está desempregada) nas seis principais regiões metropolitanas brasileiras nos meses de julho de 2006 a julho de 2011.

Suponha que a razão entre as taxas de desemprego de julho de 2010 e julho de 2011 seja igual à razão entre a taxa de desemprego de julho de 2011 e julho de 2012.
A taxa de desemprego em julho de 2012 será um número entre
[tex] razão_{(julho 2010/julho 2011)} =\ razão_{(julho 2011/julho 2012)} [tex]
[tex] \frac{6\ –\ 9,6}{2011\ –\ 2010} =\ –1,15 [tex]
Logo,
6 + (– 1,15) = 4,85
(ENEM 2014 - 3ª Aplicação).
O quadro a seguir indica a quantidade de medalhas obtidas por atletas brasileiros nos Jogos Olímpicos de 1976 a 2008.

A mediana e a média do número de medalhas obtidas pelos atletas brasileiros nos Jogos Olímpicos de 1976 a 2008 são, respectivamente, iguais a
Ordenando os dados: 2 - 3 - 4 - 6 - 8 - 10 - 12 - 15 - 15
Mediana: 2 - 3 - 4 - 6 - 8 - 10 - 12 - 15 - 15
média: [tex] \frac{2 + 3 + 4 + 6 + 8 + 10 + 12 + 15 + 15}{9} = \frac{75}{9} = 8,333.... [tex]
(ENEM 2014 - 3ª Aplicação).
A legislação brasileira estabelece vários impostos para que o Estado levante os recursos necessários para custear os investimentos e despesas de responsabilidade do setor público. A arrecadação do Brasil, nas três esferas da administração pública (municípios, estados e União), vem aumentando consideravelmente nos últimos anos. No ano de 2005, foram arrecadados cerca de 700 bilhões de reais. A evolução do crescimento da arrecadação até 2010, em porcentagem, está expressa na tabela a seguir.

De acordo com os dados apresentados, infere-se que o valor mais aproximado da arrecadação brasileira do setor público do ano de 2007 foi, em bilhões de reais, de
2005 → 700 bilhões
2006 → 700 bilhões × 1,12 = 784 bilhões
2007 → 784 bilhões × 1,12 = 878,08 bilhões
(ENEM 2014 - 3ª Aplicação).
Em Economia, costuma-se representar o consumo mensal C de uma família por uma função linear C = C₀ + (C₁Y, em que C₀ é o consumo independente da renda, (C é a chamada propensão ao consumo e Y é a renda mensal da família.
Uma determinada família possui a seguinte função consumo: C = 500 + 0,8Y. Nesse caso, ela possui um gasto de R$ 500,00, independente da renda, e propensão ao consumo de 0,8. Nessa família, a renda mensal provém somente dos salários do pai e da mãe, que são, respectivamente, R$ 3 000,00 e R$ 4 000,00
Qual o consumo mensal dessa família?
Consumo:
C = 500 + 0,8Y
C = 500 + 0,8 ∙ (3 000 + 4 000)
C = 500 + 0,8 ∙ 7 000
C = 500 + 5 600
C = 6 100,00
(ENEM 2014 - 3ª Aplicação).
O Índice Nacional de Preços ao Consumidor Amplo (IPCA) mede a variação dos custos dos gastos no período do primeiro ao último dia de cada mês de referência. O quadro a seguir mostra informações sobre o IPCA dos meses de janeiro a outubro de 2011.

De acordo com as informações dadas, a mediana e a média aritmética do IPCA, de janeiro a outubro de 2011, são, respectivamente,
Ordenando os dados: 0,15 - 0,16 - 0,37 - 0,43 - 0,47 - 0,53 - 0,77 - 0,79 - 0,80 - 0,83
Mediana = [tex] \frac{0,47\ +\ 0,53}{2} = \frac{1}{2} = 0,5 [tex]
Média:
[tex] M = \frac{0,15 + 0,16 + 0,37 + 0,43 + 0,47 + 0,53 + 0,77 + 0,79 + 0,80 + 0,83}{10} [tex]
[tex] M = \frac{ 5,3}{10} = 0,53 [tex]
(ENEM 2014 - 3ª Aplicação).
Na figura, estão indicadas as medidas reais da largura e do comprimento de uma casa.

Um arquiteto fez a planta dessa casa numa folha de papel retangular utilizando a escala 1 : 30, deixando 6 cm em cada uma das margens da folha (direita, esquerda, inferior e superior).
Quais são, respectivamente, o comprimento e a largura, em centímetros, da folha de papel utilizada?
Escala: 1 : 30 → 1cm : 30 cm
Comprimento:
[tex] C = \frac{1 500\ cm}{30} = 50 cm [tex]
→ 50 cm + 6 cm + 6 cm = 62 cm
Largura:
[tex] L = \frac{900\ cm}{30} = 30 cm [tex]
→ 30 cm + 6 cm + 6 cm = 42 cm
(ENEM 2014 - 3ª Aplicação).
Enchem-se, segundo vazões constantes e idênticas, dois reservatórios, um em forma de um cilindro circular reto e outro em forma de prisma reto de base quadrada, cujo lado da base tem a mesma medida do diâmetro da base do primeiro reservatório.

O gráfico que representa a variação das alturas dos níveis da água do reservatório cilíndrico (h₁) e do reservatório em forma de prisma (h₂) em função do volume de água contido em cada um dos reservatórios (V) estão melhor representados em

Opção B.
(ENEM 2014 - 3ª Aplicação).
No ano de 2011, o sul do país foi castigado por uma forte estiagem. Para amenizar essa situação, a prefeitura de um município dessa região utilizou um caminhão pipa, com capacidade de 32 mil litros de água para abastecer as residências de uma localidade desse município. Nessa localidade, com o caminhão pipa cheio, foram realizados 3 abastecimentos de água. No primeiro, foram distribuídos 1/4 da capacidade de água do caminhão e, no segundo 1/3 do restante.
Considerando-se que não houve desperdício de água durante o abastecimento e que o restante tenha sido utilizado totalmente, a fração da capacidade de água do caminhão pipa, distribuída no terceiro abastecimento, foi
1° abastecimento: 32 000 litros ∙ [tex]\frac{3}{4}[tex] = 24 000 litros
2° abastecimento: 24 000 litros ∙ [tex]\frac{2}{3}[tex] = 16 000 litros
3° abastecimento: [tex]\frac{16\ 000}{32\ 000}[tex] = [tex]\frac{1}{2}[tex]
(ENEM 2014 - 3ª Aplicação).
Os egípcios da Antiguidade criaram um sistema muito interessante para escrever números baseado em agrupamento.
O número 1 é representado pelo bastão |, o número 2 por dois bastões | | e assim por diante, até o número 9, representado por noves bastões em sequência | | | | | | | | | . A tabela a seguir representa alguns múltiplos de 10.

Os números de 1 a 9 999 999 na numeração egípcia derivam dos símbolos da tabela, respeitando as devidas quantidades e posições (símbolos que representam números maiores são colocados à esquerda e de maneira decrescente, são colocados os demais símbolos à direita, até a soma deles chegar ao número desejado).
Por exemplo, o numero 321 é descrito por
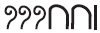
pois, 100 + 100 + 100 + 10 + 10 + 1 é igual a 321.
O número egípcio

equivale ao número
1 000 000 + 2 x 100 000 + 3 x 10 000 + 7 x 100 + 2 x 1 =
1 000 000 + 200 000 + 30 000 + 700 + 2 =
1 230 702
(ENEM 2014 - 3ª Aplicação).
A cada dia que passa, um aluno resolve 2 exercícios a mais do que resolveu no dia anterior. Ele completou seu 11º dia de estudo e resolveu 22 exercícios. Seu objetivo é resolver, no total, pelo menos 272 exercícios.
Mantendo seu padrão de estudo, quantos dias ele ainda precisa para atingir sua meta?
Temos uma P.A. com razão r = 2 e [tex]a_{11} = 22[tex].
[tex] a_{11} = a_{1} + 10 r [tex]
[tex] 22 = a_{1} + 10 \cdot 2 [tex]
[tex] a_{1} = 2 [tex]
Assim , o total de exercícios é:
Sn = 272
Logo,
[tex] a_{n} = a_{1} + (n - 1) 2 [tex]
[tex] a_{n} = 2 + 2n - 2 [tex]
[tex] a_{n} = 2n [tex]
Portanto:
[tex] S_{n} = (a_{1}\ +\ a_{2})\cdot{\frac{n}{2}} [tex]
[tex] 272 = (2 + 2n)\cdot{\frac{n}{2}} [tex]
[tex] n^{2} + n - 272 = 0 [tex]
Resolvendo a equação do 2° grau, temos:
x' = 16 e x" = – 17 (não convém)
Como já tinham se passado 11 dias, o tempo restante é 16 – 11 = 5
(ENEM 2014 - 3ª Aplicação).
A quantidade de certa espécie de crustáceos, medida em toneladas, presente num trecho de mangue, foi modelada pela equação

onde t representa o número de meses transcorridos após o início de estudo e w é uma constante.
O máximo e o mínimo de toneladas observados durante este estudo são, respectivamente,
Percebemos que o valor final depende do seno: +1 (valor máximo) e –1 (valor mínimo).
Valor Máximo = Quando o Seno atinge o valor mínimo.
[tex] \frac{600}{[6 + 4sen(wt)]} = \frac{ 600}{[6 + 4 \cdot (-1)]} = \frac{ 600}{6 – 4} = \frac{ 600}{2} = 300[tex]
Valor Mínimo = Quando o seno atinge o valor máximo.
[tex] \frac{600}{[6 + 4sen(wt)]} = \frac{ 600}{[6 + 4 \cdot (1)]} = \frac{ 600}{6 +4} = \frac{ 600}{10} = 60[tex]
(ENEM 2014 - 3ª Aplicação).
O Ibope entrevistou 100 pessoas que assistiram à estreia da versão 2011 do Rock in Rio, no dia 23 de setembro de 2011, sendo que os entrevistados atribuíram uma nota de 0 (zero) a 10 (dez) para o dia da estreia do evento. A média das notas dos entrevistados foi 9,3 e 64 pessoas deram nota 10 ao evento no dia de estreia.
Desta forma, a melhor aproximação para a média das demais notas (diferentes de 10) do dia de estreia foi
Seja [tex] S_{100} [tex] a soma das notas das 100 pessoas:
[tex] \frac{S_{100}}{100} = 9,3 [tex]
[tex] S_{64} = 640 [tex]
[tex] \frac{S_{64}\ +\ S_{36}}{100} = 9,3 [tex]
[tex] 640 + S_{36} = 930 [tex]
[tex] S_{36} = 290 [tex]
Média dessas 36 pessoas:
[tex] \frac{S36}{36} = \frac{290}{36} = 8,0555... [tex]
(ENEM 2014 - 3ª Aplicação).
A forma e as dimensões de um campo de jogo para o futebol são estabelecidas pelo Instituto Nacional de Metrologia (INMETRO), definindo no documento Regras do Jogo que o campo seja retangular e que possua os limites máximos e mínimos para largura e comprimento apresentados na figura a seguir. Estabelece também que o campo deve ser dividido em duas metades iguais e que o ponto central deve estar localizado no centro do campo. Qualquer campo que atenda a estes requisitos é considerado oficial.
Para a irrigação da área gramada do campo de jogo em determinada região do país são gastos, em média, 6 litros de água por metro quadrado por dia.

(Disponível em: . Acesso em: 30 jul. 2011 (adaptado).)
Qual será a economia semanal de água de irrigação, em litros, de um campo de futebol oficial que possua as dimensões mínimas de comprimento e de largura, em relação a um campo construído com as dimensões máximas?
75 m × 90 m = 6 750 m² → 7 x 6 litros × 6 750 = 283 500 litros de água
90 m × 120 m = 10 800 m² → 7 x 6 litros × 10 800 = 453 600 litros de água
Logo, a economia semanal é:
453 600 – 283 500 = 170 100 litros
