(Saresp).
Considere o lado do quadradinho como unidade de medida de comprimento.

Dentre as figuras desenhadas acima, a de maior perímetro é:
Calculando o perímetro (soma dos lados ou contorno) das figuras:
Figura A:
P = 4 + 1 + 3 + 5 + 1 + 6 = 20
Figura B:
P = 3 + (8 × 1) + (2 × 4) + 3 = 22
Figura C:
P = 1 × 20 = 20
Figura D:
P = 9 + 3 + 9 + 3 = 24
Portanto, opção "D".
(PAEBES).
Luciana utilizou uma fita adesiva para marcar no chão do pátio da escola a região que será utilizada para a apresentação de final de ano dos seus alunos. O desenho na malha quadriculada abaixo representa a região demarcada por Luciana.

Quantos metros de fita adesiva, no mínimo, Luciana utilizou para fazer essa marcação?
A quantidade de fita adesiva (perímetro) é:
P = 11 + 8 + (4 × 3) + 5 + 8
P = 11 + 8 + 12 + 5 + 8 = 44 metros
Portanto, opção "B".
(SPAECE).
Juliana e Ester estão fazendo um cartaz para apresentar um trabalho de Matemática. Elas colaram fita adesiva colorida ao redor desse cartaz. Observe abaixo a representação desse cartaz na malha quadriculada, onde o lado de cada quadradinho equivale a 5 cm.
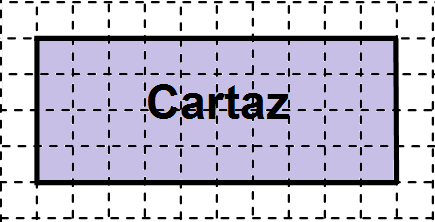
Quantos centímetros de fita, no mínimo, elas utilizaram para contornar todo esse cartaz?
A quantidade de fita adesiva (perímetro) é:
P = 5 × (10 + 4 + 10 + 4)
P = 5 × 28
P = 140 cm
Portanto, opção "C".
(SAEGO).
Para o acabamento da decoração de uma caixa de madeira, será colada uma fita de cetim em volta de sua tampa. O formato dessa tampa está representado na malha quadriculada abaixo, em que o lado de cada quadradinho equivale a 5 centímetros.

Qual deve ser o comprimento mínimo, em centímetros, dessa fita de cetim?
A quantidade mínima de fita de cetim (perímetro) é:
P = 5 × (5 + 5 + 7 + 7)
P = 5 × 24
P = 120 cm
Portanto, opção "C".
(BPW).
Uma praça de uma cidade será construída. A malha quadriculada representa o desenho da praça. Cada lado do quadradinho indica 1 metro de construção. A parte destacada está destinada ao coreto que será construído.

Quantos metros de construção serão necessários para o contorno do coreto?
O contorno do coreto (perímetro) é:
P = 3 + (7 × 1)
P = 10
Portanto, opção "D".
(PROVA BRASIL).
Uma pessoa faz caminhada em uma pista desenhada em um piso quadriculado, como a representada na figura a seguir.
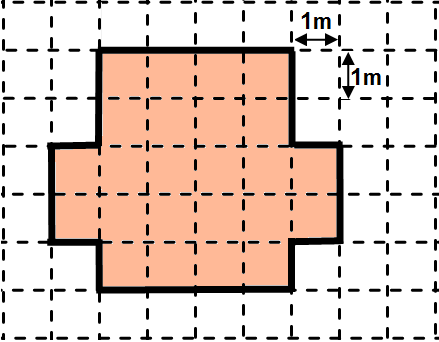
Sabendo que o lado de cada quadrado mede 1m, quantos metros essa pessoa percorre ao completar uma volta?
Uma volta nesta pista (perímetro) é:
P = (2 × 4) + (6 × 1) + (4 × 2)
P = 8 + 6 + 8
P = 22 m
Portanto, opção "C".
(SEPR).
O desenho a seguir representa o contorno do pátio de uma escola. Sabendo-se que cada quadradinho do desenho abaixo mede 2 m de lado.

Calcule quantos metros andaria uma pessoa que resolvesse contornar o pátio da escola.
Para contornar o pátio da escola (perímetro) é:
P = 2 × (2 × 12)
P = 2 × 24
P = 48 m
Portanto, opção "B".
(SARESP).
O lado de cada quadradinho da malha abaixo mede 1 cm.

Das figuras desenhadas na malha, a que possui perímetro igual a 12 cm é
Calculando o perímetro de cada figura:
A) P = 12 × 1 = 12 cm
B) P = (10 × 1) + (2 × 2) = 10 + 4 = 14 cm
C) P = (12 × 1) + 2 = 12 + 2 = 14 cm
D) P = (4 × 1) + (3 × 2) + 4 = 4 + 6 + 4 = 14 cm
Portanto, opção "A".





Nenhum comentário:
Postar um comentário