(SARESP).
Alice montou, com retalhos de tecido, um tapete como o representado a seguir. Cada quadradinho é um retalho com 10 cm de lado.

A área ocupada pelo tapete é de:
Como o lado da malha quadriculada mede 10 cm e o tapete tem (13 × 9 = 117 quadradinhos). Então:
[tex] Área = (10 × 10) × 117 [tex]
[tex] Área = 100 × 117 [tex]
[tex] Área = 11\ 700\ cm^{2} [tex]
Portanto, opção "D".
(SAERO).
Marcela fez um desenho da sua horta na malha quadriculada abaixo e pintou de amarelo. Nessa malha, o lado de cada quadradinho corresponde a 1 m.

Qual é a medida da área dessa horta?
Como o lado da malha quadriculada mede 1 cm. Então:
[tex] Área = (base × altura) [tex]
[tex] Área = 5 × 3 [tex]
[tex] Área = 15\ cm^{2} [tex]
Portanto, opção "A".
(BPW).
Observe a figura a seguir:
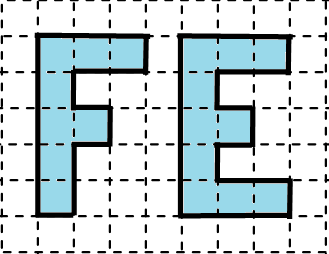
Utilizando como unidade de medida, o quadrinho do papel quadriculado, a área da palavra “FÉ” é igual a:
Como o lado da malha quadriculada mede 1 cm. Então, a área é o número de quadradinhos. Logo:
[tex] Área = (1 × 1) × 18 [tex]
[tex] Área = 18\ cm^{2} [tex]
Portanto, opção "A".
(Sobral-CE).
Observe as figuras representadas na malha quadriculada abaixo.

Qual das figuras tem a mesma área da figura representada pela letra W?
Como a área é o número de quadradinhos. Logo:
[tex] Área_{(W)} = 8\ quadradinhos [tex]
[tex] Área_{(Y)} = 8,5\ quadradinhos [tex]
[tex] Área_{(X)} = 8\ quadradinhos [tex]
[tex] Área_{(K)} = 8,5\ quadradinhos [tex]
[tex] Área_{(Z)} = 8,5\ quadradinhos [tex]
Portanto, opção "A".
(AREAL).
Observe os desenhos na malha quadriculada abaixo.

Qual desses desenhos tem a maior medida de área?
Como a área é o número de quadradinhos. Logo:
[tex] Área_{(1)} = 9\ quadradinhos [tex]
[tex] Área_{(2)} = 12\ quadradinhos [tex]
[tex] Área_{(3)} = 8\ quadradinhos [tex]
[tex] Área_{(4)} = 16\ quadradinhos [tex]
Portanto, opção "D".
(SADEAM).
Observe abaixo a figura que a professora Sandra fez em uma malha quadriculada. A medida da área de cada quadradinho dessa malha é igual a 1 cm².
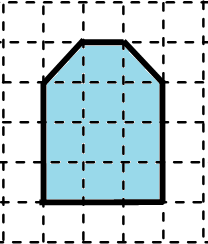
A medida da área dessa figura, em cm², é igual a
Como cada quadrinho mede 1 cm². Logo:
[tex] Área = 11\ cm^{2} [tex]
Portanto, opção "B".
(AVALIE).
Joana está tecendo um tapete de crochê que está representado na malha quadriculada abaixo.

A parte colorida de vermelho representa a parte do tapete que ela já fez. O lado do quadradinho da malha corresponde a 1 metro.
Quantos metros quadrados faltam para Joana tecer e terminar esse tapete?
Como o lado da malha quadriculada mede 1 m. Então, a área que falta é o número de quadradinhos em branco. Logo:
[tex] Área = (1 × 1) × 8 [tex]
[tex] Área = 8\ m^{2} [tex]
Portanto, opção "C".
(SPAECE).
O prefeito de uma cidade resolveu reformar a praça da igreja, construindo um jardim ao redor dessa praça. O jardim corresponde à área destacada na malha quadriculada abaixo.

Considerando que o lado de cada quadrado dessa malha corresponde a 1 m, qual é a medida da área total desse jardim?
Como o lado da malha quadriculada mede 1 m. Então, a área destinada ao jardim é o número de quadradinhos em verde. Logo:
[tex] Área = (1 × 1) × 46 [tex]
[tex] Área = 46\ m^{2} [tex]
Portanto, opção "C".
(SAEP 2013).
Cada quadradinho na malha quadriculada abaixo mede um centímetro quadrado de área.

A miniatura do campo de futebol desenhado na malha quadriculada acima é composta de
Como o lado da malha quadriculada mede 1 cm. Então, a área da miniatura do campo de futebol é:
[tex] Área = 11 × 7 [tex]
[tex] Área = 77\ cm^{2} [tex]
Portanto, opção "C".
(PAEBES).
Observe, na malha quadriculada abaixo, o desenho de uma galinha que Andréa fez na aula de Artes. O lado de cada quadradinho dessa malha quadriculada equivale a 1 cm.
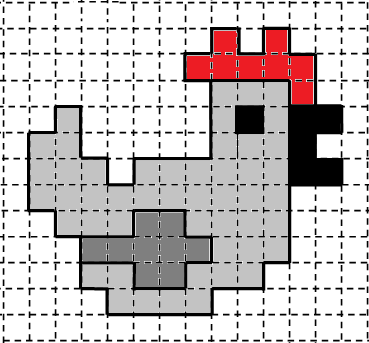
Qual é a medida da área dessa galinha que Andréa fez?
Como o lado da malha quadriculada mede 1 cm. Então, a área dessa galinha que Andréa fez é:
[tex] Área = (1 × 1) × 72 [tex]
[tex] Área = 72\ cm^{2} [tex]
Portanto, opção "D".
(SAEP 2013).
O piso da sala de Fernando está sendo coberto com cerâmica quadrada e já foram colocadas 12 peças de cerâmica.

O número de peças de cerâmicas que ainda faltam ser colocadas é
O número de peças de cerâmicas que ainda faltam ser colocadas são as cerâmicas brancas da figura. Logo:
[tex] N°\ de\ cerâmicas = 12 [tex]
Portanto, opção "C".
(SAEMI).
Veja na malha quadriculada abaixo as figuras que Carlos, Davi, Tales e Lucas desenharam.

Sabendo que cada lado do quadradinho dessa malha mede 1 cm, quem desenhou a figura de maior área?
Como o lado da malha quadriculada mede 1 cm. Então, a área é o número de quadradinhos. Logo:
Carlos: 4 quadradinhos
Davi: 4 quadradinhos
Tales: 1 quadradinho
Lucas: 10 quadradinhos
Portanto, opção "C".

Nenhum comentário:
Postar um comentário