(ENEM 2022 - 1ª Aplicação).
Em uma universidade, atuam professores que estão enquadrados funcionalmente pela sua maior titulação: mestre ou doutor. Nela há, atualmente, 60 mestres e 40 doutores. Os salários mensais dos professores mestres e dos doutores são, respectivamente, R$ 8.000,00 e R$ 12.000,00.
A diretoria da instituição pretende proporcionar um aumento salarial diferenciado para o ano seguinte, de tal forma que o salário médio mensal dos professores dessa instituição não ultrapasse R$ 12.240,00. A universidade já estabeleceu que o aumento salarial será de 25% para os mestres e precisa ainda definir o percentual de reajuste para os doutores.
Mantido o número atual de professores com suas atuais titulações, o aumento salarial, em porcentagem, a ser concedido aos doutores deverá ser de, no máximo,
Aumentando o salário dos professores mestres em 25% e aumentado, percentualmente, o salário dos professores doutores em p, temos:
[tex] \frac{60\ \cdot\ 8\ 000\ \cdot\ 1,25\ +\ 40\ \cdot\ 12\ 000\ \cdot (1\ +\ p)}{100} ≤ 12\ 240 [tex]
[tex] 600\ 000 + 480\ 000 \cdot (1\ +\ p) ≤ 12\ 240 \cdot 100 [tex]
[tex] 480\ 000 \cdot (1\ +\ p) ≤ 1\ 224\ 000\ -\ 600\ 000 [tex]
[tex] 480\ 000 \cdot (1\ +\ p) ≤ 624\ 000 [tex]
[tex] 1\ +\ p ≤ \frac{624\ 000}{480\ 000} [tex]
[tex] 1\ +\ p ≤ 1,3 [tex]
[tex] p ≤ 1,3 - 1 [tex]
[tex] p ≤ 0,3 = 30 \% [tex]
Logo, os professores doutores poderão ter um aumento salarial de no máximo 30%.
Portanto, alternativa "D".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Um borrifador de atuação automática libera, a cada acionamento, uma mesma quantidade de inseticida. O recipiente desse produto, quando cheio, contém 360 mL de inseticida, que duram 60 dias se o borrifador permanecer ligado ininterruptamente e for acionado a cada 48 minutos.
A quantidade de inseticida que é liberada a cada acionamento do borrifador, em mililitro, é
Como 60 dias tem 60 ∙ 24 ∙ 60 = 86 400 minutos, e o borrifador é acionado a cada 48 minutos, temos que a quantidade de borrifadas é dado por:
[tex] 86\ 400 ÷ 48 = 1\ 800 [tex]
Assim, sendo que o recipiente contém 360 mL, temos que a cada borrifada a quantidade de inseticida liberada é igual a:
[tex] \frac{360}{1\ 800} = 0,2\ mL [tex]
Portanto, alternativa "B".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Definem-se o dia e o ano de um planeta de um sistema solar como sendo, respectivamente, o tempo que o planeta leva para dar 1 volta completa em torno de seu próprio eixo de rotação e o tempo para dar 1 volta completa em tomo de seu Sol.
Suponha que exista um planeta Z, em algum sistema solar, onde um dia corresponda a 73 dias terrestres e que 2 de seus anos correspondam a 1 ano terrestre. Considere que 1 ano terrestre tem 365 de seus dias.
No planeta Z, seu ano corresponderia a quantos de seus dias?
I) Como 2 anos do planeta Z corresponde a 1 ano terrestre que tem 365 dias, temos então que 1 ano do planeta Z corresponde a 182,5 dias terrestres.
II) Como 1 dia do planeta Z corresponde a 73 dias terrestres, temos:
[tex] dias\ do\ planeta\ ----- Z\ dias\ terrestres[tex]
[tex]1\ ----- 73 [tex]
[tex] x\ ----- 182,5\ (1\ ano\ no\ planeta\ Z) [tex]
[tex]73x = 182,5 [tex]
[tex]x = \frac{182,5}{73} [tex]
[tex]x = 2,5\ dias [tex]
Assim, temos x = 2,5 dias.
Portanto, alternativa "A".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Em uma competição de velocidade, diz-se que há uma ultrapassagem quando um veículo que está atrás de outro passa à sua frente, com ambos se deslocando no mesmo sentido. Considere uma competição automobilística entre cinco carros em uma pista com 100 m de comprimento, onde todos largam no mesmo instante e da mesma linha. O gráfico mostra a variação da distância percorrida por cada veículo, em função do tempo, durante toda a competição.

Qual o número de ultrapassagens, após o início da competição, efetuadas pelo veículo que chegou em último lugar?
Pelo gráfico, o veículo que chegou em último colocado não ultrapassou nenhum outro veículo, porém foi ultrapassado duas vezes.

Portanto, alternativa "A".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Em uma loja, o preço promocional de uma geladeira é de R$ 1 000,00 para pagamento somente em dinheiro. Seu preço normal, fora da promoção, é 10% maior. Para pagamento feito com o cartão de crédito da loja, é dado um desconto de 2% sobre o preço normal.
Uma cliente decidiu comprar essa geladeira, optando pelo pagamento com o cartão de crédito da loja. Ela calculou que o valor a ser pago seria o preço promocional acrescido de 8%. Ao ser informada pela loja do valor a pagar, segundo sua opção, percebeu uma diferença entre seu cálculo e o valor que lhe foi apresentado.
O valor apresentado pela loja, comparado ao valor calculado pela cliente, foi
O preço normal da geladeira é 1000 ∙ 1,1 = 1100 reais. Pagando com cartão de crédito, o valor passa a ser: 1 100 ∙ 1,02 = 1078 reais.
Segundo o cálculo da cliente, pagando com o cartão de crédito, ela pagará 1000 ∙ 1,08 = 1080 reais. Dessa forma, o valor apresentado pela loja corresponde a 1080 – 1078 = 2 reais a menos que o valor calculado pela cliente.
Portanto, alternativa "A".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Uma pessoa precisa se deslocar de automóvel do ponto P para o ponto Q, indicados na figura, na qual as linhas verticais e horizontais simbolizam ruas.

Por causa do sentido de tráfego nessas ruas, o caminho poligonal destacado é a possibilidade mais curta de efetuar esse deslocamento. Para descrevê-lo, deve-se especificar qual o sentido a ser tomado em cada cruzamento de ruas, em relação à direção de deslocamento do automóvel, que se movimentará continuamente. Para isso, empregam-se as letras E, F e D para indicar “vire à esquerda”, “siga em frente” e “vire à direita”, respectivamente.
A sequência de letras que descreve o caminho poligonal destacado é
Empregando as letras E para indicar “vire à esquerda”, F para indicar “siga em frente” e D para indicar “vire à direita”, a sequência de letras que descreve o caminho poligonal é DFEFDDEEFFD.

Portanto, alternativa "C".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Uma loja comercializa cinco modelos de caixas-d’água (I, II, III, IV e V), todos em formato de cilindro reto de base circular. Os modelos II, III, IV e V têm as especificações de suas dimensões dadas em relação às dimensões do modelo I, cuja profundidade é P e área da base é [tex]A_{b} [tex], como segue:
• modelo II: o dobro da profundidade e a metade da área da base do modelo I;
• modelo III: o dobro da profundidade e a metade do raio da base do modelo I;
• modelo IV: a metade da profundidade e o dobro da área da base do modelo I;
• modelo V: a metade da profundidade e o dobro do raio da base do modelo I.
Uma pessoa pretende comprar nessa loja o modelo de caixa-d’água que ofereça a maior capacidade volumétrica. O modelo escolhido deve ser o
Seja [tex]R_{b} [tex] o raio da base do cilindro I que tem área da base [tex]A_{b} [tex] e profundidade (altura) P.
Os volumes VI , VII, VIII, VIV e VV, dos cilindros I; II; III; IV e V, respectivamente, são dados por:
[tex]V_{(I)} = A_{b} \cdot P [tex]
[tex]V_{(II)} = \frac{A_{b}}{2} \cdot 2P = A_{b} \cdot P [tex]
[tex]V_{(III)} = π \cdot (\frac{R_{b}}{2})^{2} \cdot 2P = \frac{π\ R_{b}^{2}}{4} \cdot 2P = \frac{A_{b}\ \cdot\ P}{2} [tex]
[tex]V_{(IV)} = 2 \cdot A_{b} \cdot \frac{P}{2} = A_{b} \cdot P [tex]
[tex]V_{(V)} = π \cdot (2 \cdot R_{b})^{2} \cdot \frac{P}{2} = 4π R_{b}^{2} \cdot \frac{P}{2} = 2 \cdot A_{b} \cdot P [tex]
Portanto, alternativa "E".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
No período de 2005 a 2013, o valor de venda dos imóveis em uma cidade apresentou alta, o, que resultou no aumento dos aluguéis. Os gráficos apresentam a evolução desses valores, para um mesmo imóvel, no mercado imobiliário dessa cidade.
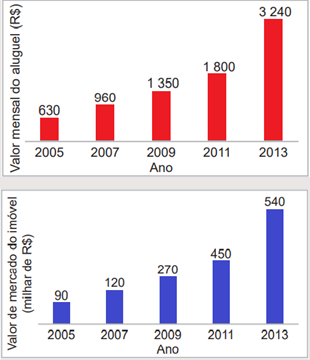
A rentabilidade do aluguel de um imóvel é calculada pela razão entre o valor mensal de aluguel e o valor de mercado desse imóvel.
Com base nos ‘dados fornecidos, em que ano a rentabilidade do aluguel foi maior?
A rentabilidade do aluguel de um imóvel é calculada pela razão:
Ano 2005: [tex] Razão = \frac{630}{90} = 7 [tex]
Ano 2007: [tex] Razão = \frac{960}{120} = 8 [tex]
Ano 2009: [tex] Razão = \frac{1\ 350}{270} = 5 [tex]
Ano 2011: [tex] Razão = \frac{1\ 800}{450} = 4 [tex]
Ano 2013: [tex] Razão = \frac{63\ 240}{540} = 6 [tex]
A rentabilidade do aluguel foi maior no ano de 2007.
Portanto, alternativa "B".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Ao escutar a notícia de que um filme recém-lançado arrecadou, no primeiro mês de lançamento, R$ 1,35 bilhão bilheteria, um estudante escreveu corretamente o número que representa essa quantia, com todos os seus algarismos.
O número escrito pelo estudante foi
O número 1,35 bilhão escrito com todos os seus algarismos é 1 350 000 000,00.
Portanto, alternativa "E".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
O governo de um estado pretende realizar uma obra de infraestrutura para auxiliar na integração e no processo de escoamento da produção agrícola de duas cidades. O projeto consiste na interligação direta das cidades, A e B com a Rodovia 003, pela construção das Rodovias 001 e 002. As duas rodovias serão construídas em linha reta e deverão se conectar a Rodovia 003 em um mesmo ponto, conforme esboço apresentado na figura, na qual estão também indicadas as posições das cidades A e B, considerando o eixo x posicionado sobre a Rodovia 003, e cinco localizações sugeridas para o ponto de conexão entre as três rodovias.

Pretende-se que a distância percorrida entre as duas cidades, pelas Rodovias 001 e 002, passando pelo ponto de conexão, seja a menor possível.
Dadas as exigências do projeto, qual das localizações sugeridas deve ser a escolhida para o ponto de conexão?
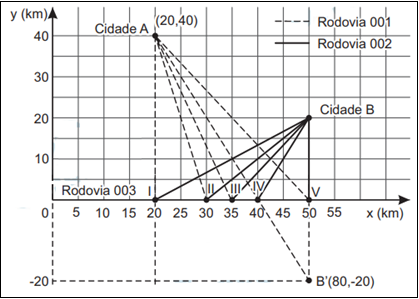
I) Sejam A(20; 40) e B(50; 20) os pontos associados as cidades A e B, respectivamente.
II) O ponto B’(50; – 20) é o simétrico de B em relação à rodovia 003.
III) O ponto P(xp; 0) de conexão pertence à rodovia 003. Assim, A, B’ e P estão alinhados. Assim,

Portanto, alternativa "D".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Uma pessoa precisa contratar um operário para fazer um serviço em sua casa. Para isso, ela postou um anúncio em uma rede social. Cinco pessoas responderam informando preços por hora trabalhada, gasto diário com transporte e tempo necessário para conclusão do serviço, conforme valores apresentados no quadro.
| Operário | Preço por hora (real) | Preço do transporte (real) | Tempo até conclusão (hora) |
|---|---|---|---|
| I | 120 | 0,00 | 8 |
| II | 180 | 0,00 | 6 |
| III | 170 | 20,00 | 6 |
| IV | 110 | 10,00 | 9 |
| V | 110 | 0,00 | 10 |
Se a pessoa pretende gastar o mínimo possível com essa contratação, irá contratar o operário
Observe a tabela a seguir:

Se a pessoa pretende gastar o mínimo possível, deverá contratar o operário I.
Portanto, alternativa "A".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Uma cozinheira produz docinhos especiais por encomenda. Usando uma receita-base de massa, ela prepara uma porção, com a qual produz 50 docinhos maciços de formato esférico, com 2 cm de diâmetro. Um cliente encomenda 150 desses docinhos, mas pede que cada um tenha formato esférico com 4 cm de diâmetro. A cozinheira pretende preparar o número exato de porções da receita-base de massa necessário para produzir os docinhos dessa encomenda.
Quantas porções da receita-base de massa ela deve preparar para atender esse cliente?
Seja V o volume, em centímetros cúbicos, de massa da receita-base para a produção de 50 docinhos de formato esférico com 2cm de diâmetro.
[tex]V_{1} = \frac{4\ \cdot\ π\ \cdot\ R^{2}}{3} \cdot\ 50 = \frac{4\ \cdot\ π\ \cdot 1^{3}}{3} \cdot\ 50 = \frac{200 π}{3} [tex]
Para a encomenda de 150 desses docinhos, com 4 cm de diâmetro, devemos ter:
[tex]V_{2} = \frac{4\ \cdot\ π\ \cdot\ R^{2}}{3} \cdot\ 150 = \frac{4\ \cdot\ π\ \cdot 2^{3}}{3} \cdot\ 150 = 1\ 600π [tex]
Agora, encontrar a quantidade de porções da receita-base:
[tex] \frac{V_{2}}{V_{1}} = \frac{1\ 600π}{\frac{200\ π}{3}} = 1\ 600π \cdot \frac{3}{200\ π} = 24 [tex]
Dessa forma a cozinheira deve preparar 24 porções da receita-base para atender esse cliente.
Portanto, alternativa "E".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Uma empresa produz e vende um tipo de chocolate, maciço, em formato de cone circular reto com as medidas do diâmetro da base e da altura iguais a 8 cm e 10 cm, respectivamente, como apresenta a figura.

Devido a um aumento de preço dos ingredientes utilizados na produção desse chocolate, a empresa decide produzir esse mesmo tipo de chocolate com um volume 19% menor, no mesmo formato de cone circular reto com altura de 10 cm.
Para isso, a empresa produzirá esses novos chocolates com medida do raio da base, em centímetro, igual a
I) Seja [tex]V_{1} [tex] o volume do chocolate, em centímetros cúbicos, do cone circular reto com raio da base e altura iguais a 4 cm e 10 cm, respectivamente.
[tex]V_{1} = \frac{π\ \cdot\ R^{2} \cdot\ h}{3} = \frac{π\ \cdot\ 4^{2} \cdot\ 10}{3} = \frac{160π}{3} [tex]
II) Sendo [tex]V_{2} [tex] o volume de chocolate, em centímetros cúbicos, do cone circular reto com raio da base e altura iguais a R cm e 10 cm, respectivamente, de acordo com o enunciado:
[tex] V_{2} = 81 \%\ \cdot V_{1} [tex]
[tex] \frac{π\ \cdot\ R^{2}\ \cdot\ h}{3} = 81 \%\ \cdot\ \frac{160π}{3} [tex]
[tex] R^{2} \cdot\ 10 = 0,81 \cdot 160 [tex]
[tex] R^{2} = \frac{129,6}{10} [tex]
[tex] R = \sqrt{12,96} [tex]
[tex] R = 3,60\ cm [tex]
Portanto, alternativa "C".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Em janeiro de 2013, foram declaradas 1 794 272 admissões e 1 765 372 desligamentos no Brasil, ou seja, foram criadas 28 900 vagas de emprego, segundo dados do Cadastro Geral de Empregados e Desempregados (Caged), divulgados pelo Ministério do Trabalho e Emprego (MTE). Segundo o Caged, o número de vagas criadas em janeiro de 2013 sofreu uma queda de 75%, quando comparado com o mesmo período de 2012.
Disponível em: http://portal.mte.gov.br. Acesso em: 23 fev. 2013 (adaptado).
De acordo com as informações dadas, o número de vagas criadas em janeiro de 2012 foi
Sendo V o número de vagas criadas em janeiro de 2012, para que o número de vagas criadas em janeiro de 2013 tenha sofrido uma queda de 75%, devemos ter:
[tex]25 \% \cdot V = 28\ 900 [tex]
[tex]0,25 \cdot V = 28\ 900 [tex]
[tex] V = \frac{28\ 900}{0,25} [tex]
[tex]V = 115\ 600[tex]
Portanto, alternativa "C".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Um prédio, com 9 andares e 8 apartamentos de 2 quartos por andar, está com todos os seus apartamentos à venda. Os apartamentos são identificados por números formados por dois algarismos, sendo que a dezena indica o andar onde se encontra o apartamento, e a unidade, um algarismo de 1 a 8, que diferencia os apartamentos de um mesmo andar. Quanto à incidência de sol nos quartos desses apartamentos, constatam-se as seguintes características, em função de seus números de identificação:
• naqueles que finalizam em 1 ou 2, ambos os quartos recebem sol apenas na parte da manhã;
• naqueles que finalizam em 3, 4, 5 ou 6, apenas um dos quartos recebe sol na parte da manhã;
• naqueles que finalizam em 7 ou 8, ambos os quartos recebem sol apenas na parte da tarde.
Uma pessoa pretende comprar 2 desses apartamentos em um mesmo andar, mas quer que, em ambos, pelo menos um dos quartos receba sol na parte da manhã.
De quantas maneiras diferentes essa pessoa poderá escolher 2 desses apartamentos para compra nas condições desejadas?
Para cada andar, o número de maneiras diferentes de escolher 2 apartamentos entre os quais, em pelo menos um dos quartos receba sol na parte da manhã é:
[tex] \frac{6!}{(6\ -\ 2)!\ × 2!}[tex]
Como o prédio possui 9 andares, o número de maneiras de escolher 2 desses apartamentos nas condições desejadas será:
[tex] 9 × \frac{6!}{(6\ -\ 2)!\ × 2!}[tex]
Portanto, alternativa "B".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Uma máquina em operação tem sua temperatura T monitorada por meio de um registro gráfico, ao longo do tempo t. Essa máquina possui um pistão cuja velocidade V varia com a temperatura T da máquina, de acordo com a expressão [tex]V = T^{2} − 4[tex]. Após a máquina funcionar durante o intervalo de tempo de 10 horas, o seu operador analisa o registro gráfico, apresentado na figura, para avaliar a necessidade de eventuais ajustes, sabendo que a máquina apresenta falhas de funcionamento quando a velocidade do pistão se anula.

Quantas vezes a velocidade do pistão se anulou durante as 10 horas de funcionamento?
A velocidade se anula para T = –2°C ou T = 2°C, pois:
[tex]V = T^{2} − 4 ⇔ T = ± 2 [tex]
A partir do gráfico a seguir, a velocidade no pistão se anulou 5 vezes durante as 10 horas de funcionamento nos pontos A, B, C, D e E.

Portanto, alternativa "E".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
A World Series é a decisão do campeonato norte-americano de beisebol. Os dois times que chegam a essa fase jogam, entre si, até sete partidas. O primeiro desses times que completar quatro vitórias é declarado campeão. Considere que, em todas as partidas, a probabilidade de qualquer um dos dois times vencer é sempre [tex] \frac{1}{2}[tex].
Qual é a probabilidade de o time campeão ser aquele que venceu a primeira partida da World Series?
Seja V a probabilidade de vencer e D a probabilidade de derrota. Assim, a probabilidade de o time campeão ser aquele que venceu a primeira partida é:
[tex] \underbrace{VVV}_{3\ últimas\\ partidas}[tex] [tex]ou[tex] [tex] \underbrace{VVDV}_{4\ últimas\\ partidas}[tex] [tex]ou[tex] [tex] \underbrace{VVDDV}_{5\ últimas\\ partidas}[tex] [tex]ou[tex] [tex] \underbrace{VVDDDV}_{6\ últimas\\ partidas}[tex]
[tex]= (\frac{1}{2})^{3} + \frac{3!}{2!} \cdot (\frac{1}{2})^{4} + \frac{4!}{2!\ \cdot\ 2!} \cdot (\frac{1}{2})^{5} + \frac{5!}{2!\ \cdot\ 3!} \cdot (\frac{1}{2})^{6} [tex]
[tex]= \frac{1}{8} + \frac{3}{16} + \frac{6}{32} + \frac{10}{64} [tex]
[tex]= \frac{42}{64} [tex]
Portanto, alternativa "C".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
O gráfico apresenta os totais de receitas e despesas de uma empresa, expressos em milhão de reais, no decorrer dos meses de um determinado ano. A empresa obtém lucro quando a diferença entre receita e despesa é positiva e tem prejuízo quando essa diferença é negativa.

Qual é a mediana, em milhão de reais, dos valores dos lucros apurados pela empresa nesse ano?
A empresa obteve lucro, em milhões de reais, nos seguintes meses.
Janeiro: 6 – 3 = 3
Março: 3 – 2 = 1
Maio: 6 – 1 = 5
Junho: 5 – 2 = 3
Julho: 6 – 4 = 2
Setembro: 7 – 3 = 4
Novembro: 8 – 7 = 1
Dezembro: 6 – 2 = 4
O rol é (ordem crescente):
1 , 1 , 2 , 3 , 3 , 4 , 4 , 5
Logo, a mediana é:
[tex] Me = \frac{3\ +\ 3}{2} = \frac{6}{2} = 3[tex]
Portanto, alternativa "D".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
O pacote básico de um jogo para smartphone, que é vendido a R$ 50,00, contém 2 000 gemas e 100 000 moedas de ouro, que são itens utilizáveis nesse jogo. A empresa que comercializa esse jogo decidiu criar um pacote especial que será vendido a R$ 100,00 e que se diferenciará do pacote básico por apresentar maiores quantidades de gemas e moedas de ouro. Para estimular as vendas desse novo pacote, a empresa decidiu inserir nele 6 000 gemas a mais, em relação ao que o cliente teria caso optasse por comprar, com a mesma quantia, dois pacotes básicos.
A quantidade de moedas de ouro que a empresa deverá inserir ao pacote especial, para que seja mantida a mesma proporção existente entre as quantidades de gemas e de moedas de ouro contidas no pacote básico, é
Se x for a quantidade de moedas de ouro que a empresa deverá inserir para manter a mesma proporção entre as gemas e as moedas de ouro contidas “em um pacote básico” então:
[tex] \frac{2\ 000}{100\ 000} = \frac{2\ \cdot\ 2\ 000\ +\ 6\ 000}{100\ 000\ +\ x} [tex]
[tex] \frac{1}{50} = \frac{10\ 000}{100\ 000\ +\ x} [tex]
[tex] 100\ 000 + x = 500\ 000 [tex]
[tex] x = 500\ 000 - 100\ 000 [tex]
[tex] x = 400\ 000 [tex]
Portanto, alternativa "E".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Um parque tem dois circuitos de tamanhos diferentes para corridas. Um corredor treina nesse parque e, no primeiro dia, inicia seu treino percorrendo 3 voltas em torno do circuito maior e 2 voltas em torno do menor, perfazendo um total de 1 800 m. Em seguida, dando continuidade a seu treino, corre mais 2 voltas em torno do circuito maior e 1 volta em torno do menor, percorrendo mais 1 100 m.
No segundo dia, ele pretende percorrer 5 000 m nos circuitos do parque, fazendo um número inteiro de voltas em torno deles e de modo que o número de voltas seja o maior possível.
A soma do número de voltas em torno dos dois circuitos, no segundo dia, será
Seja “a” o comprimento em metros da maior pista e “b” o comprimento em metros da pista menor. Assim:
[tex] \begin{cases} 3a + 2b = 1\ 800 \\ 2a + b = 1\ 100 × (-2)\end{cases} [tex]
[tex]\underline{ \begin{cases} 3a + 2b = 1\ 800 \\ -4a - 2b = - 2\ 200 \end{cases} } [tex]
[tex]-a = - 400 × (- 1) [tex]
[tex]a = 400 [tex]
Agora, encontrar b:
[tex] 2a + b = 1\ 100 [tex]
[tex] 2 \cdot 400 + b = 1\ 100 [tex]
[tex] 800 + b = 1\ 100 [tex]
[tex] b = 1\ 100 - 800 [tex]
[tex] b = 300 [tex]
No segundo dia, ele pretende percorrer 5 000 nos circuitos, fazendo x e y voltas inteiras, de modo que o número de voltas seja o maior possível, logo:
[tex] x \cdot 400 + y \cdot 300 = 5\ 000 [tex]
e assim x = 2 e y = 14, cuja soma é 2 + 14 = 16.
Portanto, alternativa "E".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Uma equipe de marketing digital foi contratada para aumentar as vendas de um produto ofertado em um site de comércio eletrônico. Para isso, elaborou um anúncio que, quando o cliente clica sobre ele, é direcionado para a página de vendas do produto. Esse anúncio foi divulgado em duas redes sociais, A e B, e foram obtidos os seguintes resultados:
• rede social A: o anúncio foi visualizado por 3 000 pessoas; 10% delas clicaram sobre o anúncio e foram redirecionadas para o site; 3% das que clicaram sobre o anúncio compraram o produto. O investimento feito para a publicação do anúncio nessa rede foi de R$ 100,00;
• rede social B: o anúncio foi visualizado por 1 000 pessoas; 30% delas clicaram sobre o anúncio e foram redirecionadas para o site; 2% das que clicaram sobre o anúncio compraram o produto. O investimento feito para a publicação do anúncio nessa rede foi de R$ 200,00.
Por experiência, o pessoal da equipe de marketing considera que a quantidade de novas pessoas que verão o anúncio é diretamente proporcional ao investimento realizado, e que a quantidade de pessoas que comprarão o produto também se manterá proporcional à quantidade de pessoas que clicarão sobre o anúncio.
O responsável pelo produto decidiu, então, investir mais R$ 300,00 em cada uma das duas redes sociais para a divulgação desse anúncio e obteve, de fato, o aumento proporcional esperado na quantidade de clientes que compraram esse produto. Para classificar o aumento obtido na quantidade (Q) de compradores desse produto, em consequência dessa segunda divulgação, em relação aos resultados observados na primeira divulgação, o responsável pelo produto adotou o seguinte critério:
• Q ≤ 60%: não satisfatório;
• 60% < Q ≤ 100%: regular;
• 100% < Q ≤ 150%: bom;
• 150% < Q ≤ 190%: muito bom;
• 190% < Q ≤ 200%: excelente.
O aumento na quantidade de compradores, em consequência dessa segunda divulgação, em relação ao que foi registrado com a primeira divulgação, foi classificado como
Na primeira divulgação houve:
(1) Rede social A (investimento de R$ 100,00)
3 000 visualizações;
[tex]10 \%\ \cdot 3\ 000 = \frac{10}{100} \cdot 3\ 000 = 300\ pessoas\ clicaram [tex]
e
[tex]3 \%\ \cdot 300 = \frac{3}{100} \cdot 300 = 9\ pessoas\ compraram [tex]
(2) Rede social B (investimento de R$ 200,00)
1 000 visualizações;
[tex]30 \%\ \cdot 1\ 000 = \frac{30}{100} \cdot 1\ 000 = 300\ pessoas\ clicaram [tex]
e
[tex]2 \%\ \cdot 300 = \frac{2}{100} \cdot 300 = 6\ pessoas\ compraram [tex]
Na segunda divulgação, considerando o aumento proporcional esperado houve:
(1) Rede social A (investimento de R$ 300,00) como o investimento foi 3 vezes maior, obteve 3 × 9 = 27 compradores.
(2) Rede social B ( investimento de R$ 300,00) como o investimento foi 1,5 vezes maior, obteve 1,5 × 6 = 9 compradores.
O aumento obtido na quantidade (Q) em consequência da segunda divulgação, em relação aos resultados observados na primeira divulgação foi:
[tex] \frac{(27\ +\ 9)\ -\ (9\ -\ 6)}{9\ +\ 6} = \frac{21}{15} = 1,40 = 140 \%[tex]
e, pelo critério adotado, classificado como bom, pois [tex]100 \% < Q ≤ 150 \%[tex].
Portanto, alternativa "C".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Uma montadora de automóveis divulgou que oferta a seus clientes mais de 1 000 configurações diferentes de carro, variando o modelo, a motorização, os opcionais e a cor do veículo. Atualmente, ela oferece 7 modelos de carros com 2 tipos de motores: 1.0 e 1.6. Já em relação aos opcionais, existem 3 escolhas possíveis: central multimídia, rodas de liga leve e bancos de couro, podendo o cliente optar por incluir um, dois, três ou nenhum dos opcionais disponíveis.
Para ser fiel à divulgação feita, a quantidade mínima de cores que a montadora deverá disponibilizar a seus clientes é
A montadora oferece 7 modelos, 2 tipos de motores e 3 opções de opcionais.
O cliente pode optar por incluir um, dois, três ou nenhum dos opcionais disponíveis. Dessa forma ele tem:
[tex]C_{3,1} + C_{3,2} + C_{3,3} + C_{3,0} = 3 + 3 + 1 + 1 = 8[tex] maneiras de fazer essa inclusão.
Seja x a quantidade mínima de cores disponíveis. Temos que:
[tex]\frac{7}{modelos} \cdot \frac{2}{motoes} \cdot \frac{8}{opcionais} \cdot \frac{x}{cores} > 1\ 000 [tex]
[tex]112x > 1\ 000 [tex]
[tex]x > \frac{1\ 000}{112} [tex]
[tex]x > 8,92 [tex]
Logo, a quantidade mínima de cores para que a montadora tenha mais de 1000 configurações diferentes é 9.
Portanto, alternativa "B".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Dentre as diversas planificações possíveis para o cubo, uma delas é a que se encontra apresentada na Figura 1.

Em um cubo, foram pintados, em três de suas faces, quadrados de cor vermelha, que ocupam um quarto dessas faces, tendo esses três quadrados um vértice em comum, conforme ilustrado na Figura 2.

A planificação do cubo da Figura 2, conforme o tipo de planificação apresentada na Figura 1, é

Ao planificarmos o cubo acima, obtemos a seguinte planificação:
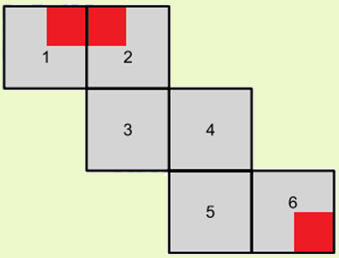
Portanto, alternativa "E".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Cada número que identifica uma agência bancária tem quatro dígitos: [tex]N_{1}[tex], [tex]N_{2}[tex], [tex]N_{3}[tex], [tex]N_{4}[tex] mais um dígito verificador [tex]N_{5}[tex].

Todos esses dígitos são números naturais pertencentes ao conjunto {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Para a determinação de N5, primeiramente multiplica-se ordenadamente os quatro primeiros dígitos do número da agência por 5, 4, 3 e 2, respectivamente, somam-se os resultados e obtém-se:
[tex] S = 5 N_{1} + 4 N_{2} + 3 N_{3} + 2 N_{4}[tex].
Posteriormente, encontra-se o resto da divisão de S por 11, denotando por R esse resto. Dessa forma, [tex]N_{5}[tex] é a diferença [tex]11 − R[tex].
Considere o número de uma agência bancária cujos quatro primeiros dígitos são 0100.
Qual é o dígito verificador [tex]N_{5}[tex] dessa agência bancária?
Multiplicamos os 4 primeiros dígitos, respectivamente, por 5, 4, 3 e 2. Fazemos a soma (S) dos resultados:
[tex] S = 5 N_{1} + 4 N_{2} + 3 N_{3} + 2 N_{4}[tex]
Considerando os quatro primeiros dígitos do número da agência, sendo 0100, teremos:
[tex] S = 5 \cdot 0 + 4 \cdot 1 + 3 \cdot 0 + 2 \cdot 0 = 4 [tex]
Sabe-se que [tex]N_{5} = 11\ –\ R[tex], onde R é o resto da divisão S por 11:

Logo, [tex]N_{5} = 11\ –\ 4 = 7[tex]
Portanto, alternativa "C".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Um casal está reformando a cozinha de casa e decidiu comprar um refrigerador novo. Observando a planta da nova cozinha, desenhada na escala de 1 : 50, notaram que o espaço destinado ao refrigerador tinha 3,8 cm de altura e 1,6 cm de largura. Eles sabem que os fabricantes de refrigeradores indicam que, para um bom funcionamento e fácil manejo na limpeza, esses eletrodomésticos devem ser colocados em espaços que permitam uma distância de, pelo menos, 10 cm de outros móveis ou paredes, tanto na parte superior quanto nas laterais. O casal comprou um refrigerador que caberia no local a ele destinado na nova cozinha, seguindo as instruções do fabricante.
Esse refrigerador tem altura e largura máximas, em metro, respectivamente, iguais a
Espaço em planta:

Espaço real levando em conta a escala 1 : 50.

Como devesse descontar pelo menos 10 cm nas laterais e 10 cm na parte superior, o refrigerador tem altura máxima de 1,80 m e largura máxima de 0,60 m.
Portanto, alternativa "A".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Foram convidadas 32 equipes para um torneio de futebol, que foram divididas em 8 grupos com 4 equipes, sendo que, dentro de um grupo, cada equipe disputa uma única partida contra cada uma das demais equipes de seu grupo. A primeira e a segunda colocadas de cada grupo seguem para realizar as 8 partidas da próxima fase do torneio, chamada oitavas de final. Os vencedores das partidas das oitavas de final seguem para jogar as 4 partidas das quartas de final. Os vencedores das quartas de final disputam as 2 partidas das semifinais, e os vencedores avançam para a grande final, que define a campeã do torneio.
Pelas regras do torneio, cada equipe deve ter um período de descanso de, no mínimo, 3 dias entre dois jogos por ela disputados, ou seja, se um time disputar uma partida, por exemplo, num domingo, só poderá disputar a partida seguinte a partir da quinta-feira da mesma semana.
O número mínimo de dias necessários para a realização desse torneio é
De acordo com o enunciado, para esta configuração do torneio, para que uma equipe chegue a final, ela fará um total de sete jogos. Como deve-se ter 3 dias de folga entre um jogo e outro, tem-se que os dias de jogos estão em progressão aritmética de razão 4 e primeiro termo 1.
Assim, o 7º jogo irá ocorrer no dia 25, pois:
[tex] a_{7} = a_{1} + (n - 1) \cdot r [tex]
[tex] a_{7} = 1 + (5 - 1) \cdot 6 [tex]
[tex] a_{7} = 1 + 4 \cdot 6 [tex]
[tex] a_{7} = 1 + 24 = 25 [tex]
Portanto, alternativa "B".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Em um jogo de bingo, as cartelas contêm 16 quadrículas dispostas em linhas e colunas. Cada quadrícula tem impresso um número, dentre os inteiros de 1 a 50, sem repetição de número. Na primeira rodada, um número é sorteado, aleatoriamente, dentre os 50 possíveis. Em todas as rodadas, o número sorteado é descartado e não participa dos sorteios das rodadas seguintes. Caso o jogador tenha em sua cartela o número sorteado, ele o assinala na cartela. Ganha o jogador que primeiro conseguir preencher quatro quadrículas que formam uma linha, uma coluna ou uma diagonal, conforme os tipos de situações ilustradas na Figura 1.

Preenchimento em linha Preenchimento em coluna Preenchimento em diagonal Figura 1 O jogo inicia e, nas quatro primeiras rodadas, foram sorteados os seguintes números: 03, 27, 07 e 48. Ao final da quarta rodada, somente Pedro possuía uma cartela que continha esses quatro números sorteados, sendo que todos os demais jogadores conseguiram assinalar, no máximo, um desses números em suas cartelas. Observe na Figura 2 o cartão de Pedro após as quatro primeiras rodadas.
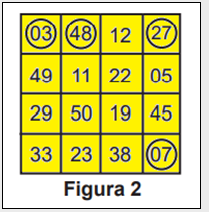
A probabilidade de Pedro ganhar o jogo em uma das duas próximas rodadas é
Pedro ganha o jogo em uma das duas próximas jogadas se conseguir preencher a linha A, na primeira ou na segunda rodada, a coluna B ou a diagonal C, como mostra a figura:

Assim, a probabilidade pedida é:
[tex] = \frac{1}{46} + \frac{45}{46} \cdot \frac{1}{45} + \frac{2}{46} \cdot \frac{1}{45} + \frac{2}{46} \cdot \frac{1}{45}[tex]
[tex] = \frac{1}{46} + \frac{49}{46 × 45} [tex]
Portanto, alternativa "E".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
O professor de artes orientou seus estudantes a realizarem a seguinte sequência de atividades:
• Dobrar uma folha de papel em formato quadrado duas vezes, em sequência, ao longo das linhas tracejadas, conforme ilustrado nas figuras 1 e 2, para obter o papel dobrado, conforme Figura 3.

• Em seguida, no papel dobrado da Figura 3, considerar o ponto R, sobre o segmento OM, sendo M o ponto médio do lado do quadrado original, de modo que [tex] OR = \frac{1}{4}OM[tex], traçar um arco de circunferência de raio medindo [tex]\frac{1}{2}OM[tex] com centro no ponto R, obtendo a Figura 4. Por último, recortar o papel ao longo do arco de circunferência e excluir a parte que contém o setor circular, obtendo o papel dobrado, conforme Figura 5.

Após desdobrado o papel que restou na Figura 5, a figura plana que os estudantes obterão será
Observe a figura a seguir:

No ΔORB temos que [tex]OB < a + 2a = 3a[tex].
Assim, [tex]OB < OA[tex].
Portanto, a figura plana que os estudantes obterão será a figura acima.
Portanto, alternativa "C".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
A esperança de vida ao nascer é o número médio de anos que um indivíduo tende a viver a partir de seu nascimento, considerando dados da população. No Brasil, esse número vem aumentando consideravelmente, como mostra o gráfico.
Esperança de vida ao nascer

Disponível em: http://cod.ibge.gov.br. Acesso em: 6 mar. 2014 (adaptado).
Pode-se observar que a esperança de vida ao nascer em 2012 foi exatamente a média das registradas nos anos de 2011 e 2013. Suponha que esse fato também ocorreu com a esperança de vida ao nascer em 2013, em relação às esperanças de vida de 2012 e de 2014.
Caso a suposição feita tenha sido confirmada, a esperança de vida ao nascer no Brasil no ano de 2014 terá sido, em ano, igual a
Seja x a esperança de vida para o ano de 2014. Assim, de acordo com o enunciado tem-se que:
[tex] \frac{x\ +\ 73,95}{2} = 74,23 [tex]
[tex] x + 73,95 = 2 \cdot 74,23 [tex]
[tex] x + 73,95 = 148,46 [tex]
[tex] x = 148,46 - 73,95 [tex]
[tex] x = 74,51 [tex]
Portanto, alternativa "B".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Na figura estão destacadas duas trajetórias sobre a superfície do globo terrestre, descritas ao se percorrer parte dos meridianos 1, 2 e da Linha do Equador, sendo que os meridianos 1 e 2 estão contidos em planos perpendiculares entre si. O plano α é paralelo ao que contém a Linha do Equador.

A vista superior da projeção ortogonal sobre o plano α dessas duas trajetórias é
Observe a figura a seguir:

As projeções ortogonais dos pontos N, A, B, S, C e D no plano α são os pontos N’, A’, B’, S’, C’ e D’ respectivamente.
Assim, a projeção ortogonal sobre o plano α das duas trajetórias é mostrada na figura.
Portanto, alternativa "E".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Nos cinco jogos finais da última temporada, com uma média de 18 pontos por jogo, um jogador foi eleito o melhor do campeonato de basquete. Na atual temporada, cinco jogadores têm a chance de igualar ou melhorar essa média. No quadro estão registradas as pontuações desses cinco jogadores nos quatro primeiros jogos das finais deste ano.
| Jogadores | Jogo 1 | Jogo 2 | Jogo 3 | Jogo 4 |
|---|---|---|---|---|
| I | 12 | 25 | 20 | 20 |
| II | 12 | 12 | 27 | 20 |
| III | 14 | 14 | 17 | 26 |
| IV | 15 | 18 | 21 | 21 |
| V | 22 | 15 | 23 | 15 |
O quinto e último jogo será realizado para decidir a equipe campeã e qual o melhor jogador da temporada.
O jogador que precisa fazer a menor quantidade de pontos no quinto jogo, para igualar a média de pontos do melhor jogador da temporada passada, é o
Sejam [tex]X_{I}[tex], [tex]X_{II}[tex], [tex]X_{III}[tex], [tex]X_{IV}[tex] e [tex]X_{V}[tex] as pontuações que os jogadores I, II, III, IV e V precisam, respectivamente. Temos:
[tex]\frac{12\ +\ 25\ +\ 20\ +\ 20\ +\ X_{I}}{5} = 18[tex]
[tex]77 + X_{I} = 5 \cdot 18[tex]
[tex] X_{I} = 90 - 77 = \color{Red}{13} [tex]
[tex]\frac{12\ +\ 12\ +\ 27\ +\ 20\ +\ X_{II}}{5} = 18[tex]
[tex]71 + X_{II} = 5 \cdot 18[tex]
[tex] X_{II} = 90 - 71 = 19[tex]
[tex]\frac{14\ +\ 14\ +\ 17\ +\ 26\ +\ X_{III}}{5} = 18[tex]
[tex]71 + X_{III} = 5 \cdot 18[tex]
[tex] X_{III} = 90 - 71 = 19[tex]
[tex]\frac{15\ +\ 18\ +\ 21\ +\ 21\ +\ X_{IV}}{5} = 18[tex]
[tex]75 + X_{IV} = 5 \cdot 18[tex]
[tex] X_{IV} = 90 - 75 = 15[tex]
[tex]\frac{22\ +\ 15\ +\ 23\ +\ 15\ +\ X_{V}}{5} = 18[tex]
[tex]75 + X_{V} = 5 \cdot 18[tex]
[tex] X_{V} = 90 - 75 = 15[tex]
Portanto, alternativa "A".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Um casal planeja construir em sua chácara uma piscina com o formato de um paralelepípedo reto retângulo com capacidade para 90 000 L de água. O casal contratou uma empresa de construções que apresentou cinco projetos com diferentes combinações nas dimensões internas de profundidade, largura e comprimento. A piscina a ser construída terá revestimento interno em suas paredes e fundo com uma mesma cerâmica, e o casal irá escolher o projeto que exija a menor área de revestimento.
As dimensões internas de profundidade, largura e comprimento, respectivamente, para cada um dos projetos, são:
• projeto I: 1,8 m, 2,0 m e 25,0 m;
• projeto II: 2,0 m, 5,0 m e 9,0 m;
• projeto III: 1,0 m, 6,0 m e 15,0 m;
• projeto IV: 1,5 m, 15,0 m e 4,0 m;
• projeto V: 2,5 m, 3,0 m e 12,0 m.
O projeto que o casal deverá escolher será o
Observe a figura a seguir:

Área a ser revestida:
[tex]A = C \cdot L + 2 \cdot L \cdot P + 2 \cdot C \cdot P [tex]
[tex]A = C \cdot L + 2 \cdot P \cdot (L + C) [tex]
Calculando a área para cada projeto:
[tex]A = C \cdot L + 2 \cdot P \cdot (L + C) [tex]
[tex]A = 2 \cdot 25 + 2 \cdot 1,8 \cdot (2 + 25) [tex]
[tex]A = 50 + 3,6 \cdot 27 = 50 + 97,2 = 147,2\ m^{2} [tex]
[tex]A = C \cdot L + 2 \cdot P \cdot (L + C) [tex]
[tex]A = 9 \cdot 5 + 2 \cdot 2 \cdot (9 + 5) [tex]
[tex]A = 45 + 4 \cdot 14 = 45 + 56 = 101\ m^{2} [tex]
[tex]A = C \cdot L + 2 \cdot P \cdot (L + C) [tex]
[tex]A = 15 \cdot 6 + 2 \cdot 1 \cdot (15 + 6) [tex]
[tex]A = 90 + 2 \cdot 21 = 90 + 42 = 132\ m^{2} [tex]
[tex]A = C \cdot L + 2 \cdot P \cdot (L + C) [tex]
[tex]A = 4 \cdot 15 + 2 \cdot 1,5 \cdot (15 + 4) [tex]
[tex]A = 60 + 3 \cdot 19 = 60 + 57 = 117\ m^{2} [tex]
[tex]A = C \cdot L + 2 \cdot P \cdot (L + C) [tex]
[tex]A = 3 \cdot 12 + 2 \cdot 2,5 \cdot (3 + 12) [tex]
[tex]A = 36 + 5 \cdot 15 = 36 + 75 = 111\ m^{2} [tex]
Dessa forma, a menor área a ser revestida é a do projeto II.
Portanto, alternativa "B".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Uma instituição de ensino superior ofereceu vagas em um processo seletivo de acesso a seus cursos. Finalizadas as inscrições, foi divulgada a relação do número de candidatos por vaga em cada um dos cursos oferecidos. Esses dados são apresentados no quadro.
| Curso | Número de vagas oferecidas | Número de candidatos por vaga |
|---|---|---|
| Administração | 30 | 6 |
| Ciências Contábeis | 40 | 6 |
| Engenharia Elétrica | 50 | 7 |
| História | 30 | 8 |
| Letras | 25 | 4 |
| Pedagogia | 25 | 5 |
Qual foi o número total de candidatos inscritos nesse processo seletivo?
Número de candidatos:
Administração: 30 ∙ 6 = 180
Engenharia Elétrica: 50 ∙ 7 = 350
História: 30 ∙ 8 = 240
Letras: 25 ∙ 4 = 100
Pedagogia: 25 ∙ 5 = 125
Total = 180 + 240 + 350 + 240 + 100 + 125 = 1 235
Portanto, alternativa "D".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Peças metálicas de aeronaves abandonadas em aeroportos serão recicladas. Uma dessas peças é maciça e tem o formato cilíndrico, com a medida do raio da base igual a 4 cm e a da altura igual a 50 cm. Ela será derretida, e o volume de metal resultante será utilizado para a fabricação de esferas maciças com diâmetro de 1 cm, a serem usadas para confeccionar rolamentos. Para estimar a quantidade de esferas que poderão ser produzidas a partir de cada uma das peças cilíndricas, admite-se que não ocorre perda de material durante o processo de derretimento.
Quantas dessas esferas poderão ser obtidas a partir de cada peça cilíndrica?
Considerando n o número de esferas obtidas:
[tex] n \cdot (volume\ da\ esfera) = Volume\ do\ cilindro [tex]
[tex] n \cdot \frac{4 π R^{3}}{3} = π R^{2} \cdot h [tex]
[tex] n \cdot \frac{4\ \cdot\ \color{Red}{π}\ \cdot\ (0,5)^{3}}{3} = \color{Red}{π} \cdot 4^{2} \cdot 50 [tex]
[tex] n \cdot \frac{\color{Red}{4}\ \cdot\ 0,125}{3} = \color{Red}{4} \cdot 4 \cdot 50 [tex]
[tex] n \cdot \frac{0,125}{3} = 4 \cdot 50 [tex]
[tex] n \cdot \frac{0,125}{3} = 200 [tex]
[tex] n = \frac{600}{0,125} [tex]
[tex] n = 4\ 800\ esferas [tex]
Portanto, alternativa "D".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Um médico faz o acompanhamento clínico de um grupo de pessoas que realizam atividades físicas diariamente. Ele observou que a perda média de massa dessas pessoas para cada hora de atividade física era de 1,5 kg. Sabendo que a massa de 1 L de água é de 1 kg, ele recomendou que ingerissem, ao longo das 3 horas seguintes ao final da atividade, uma quantidade total de água correspondente a 40% a mais do que a massa perdida na atividade física, para evitar desidratação.
Seguindo a recomendação médica, uma dessas pessoas ingeriu, certo dia, um total de 1,7 L de água após terminar seus exercícios físicos.
Para que a recomendação médica tenha efetivamente sido respeitada, a atividade física dessa pessoa, nesse dia, durou
Pelo enunciado, 1,7 L é 40% maior do que o volume de água perdido.
Sabe-se, pelo enunciado, 1,7 L tem 1,7 kg de massa.
Sendo m a massa perdida, temos, em kg:
[tex]1,7 = 140 \%\ de\ m [tex]
[tex]1,7 = \frac{140}{100} \cdot m [tex]
[tex] 170 = 140 \cdot m [tex]
[tex] m = \frac{170}{140} = \frac{17}{14} [tex]
Considerando as grandezas como diretamente proporcionais, temos:
1,5 kg –––– 1 hora = 60 min
[tex] \frac{17}{14}\ kg [tex] ––––– t minutos
[tex] 1,5t = \frac{17}{14} \cdot 60 [tex]
[tex] t = \frac{17\ \cdot\ 60}{14\ \cdot\ 1,5} [tex]
[tex] t = \frac{1\ 020}{21} = 48,57\ min = 48\ min\ +\ 34\ segundos [tex]
Portanto, alternativa "C".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Em uma sala de cinema, para garantir que os espectadores vejam toda a imagem projetada na tela, a disposição das poltronas deve obedecer à norma técnica da Associação Brasileira de Normas Técnicas (ABNT), que faz as seguintes indicações:
• Distância mínima (Dmín) entre a tela de projeção e o encosto da poltrona da primeira fileira deve ser de, pelo menos, 60% da largura (L) da tela.
• Distância máxima (Dmáx) entre a tela de projeção e o encosto da poltrona da última fileira deve ser o dobro da largura (L) da tela, sendo aceitável uma distância de até 2,9 vezes a largura (L) da tela. Para o espaçamento entre as fileiras de poltronas, é considerada a distância de 1 metro entre os encostos de poltronas em duas fileiras consecutivas.
Disponível em: www.ctav.gov.br. Acesso em: 14 nov. 2013.
Uma sala de cinema, cuja largura da tela mede 12 m, está montada em conformidade com as normas da ABNT e tem suas dimensões especificadas na figura.

Pretende-se ampliar essa sala, mantendo-se na mesma posição a tela e todas as poltronas já instaladas, ampliando-se ao máximo a sala para os fundos (área de instalação de novas poltronas), respeitando-se o limite aceitável da norma da ABNT. A intenção é aumentar, ao máximo, a quantidade de poltronas da sala, instalando-se novas unidades, iguais às já instaladas.
Quantas fileiras de poltronas a sala comportará após essa ampliação?
Para a largura da tela L = 12 m, temos:
[tex]D_{(mín)} = 0,6 \cdot 12 = 7,2\ m[tex] e
[tex]D_{(aceitável)} = 2,9 \cdot 12 = 34,8[tex].
Considerando os encostos da primeira fileira como o primeiro termo de uma PA de [tex]a_{1} = 7,2[tex] e razão [tex]r = 1[tex], temos [tex]a_{n} = 34,2[tex], pois [tex]a_{n} ≤ 34,8[tex].
Logo:
[tex] a_{n} = a_{1} + (n - 1) \cdot r [tex]
[tex] 34,2 = 7,2 + (n - 1) \cdot 1 [tex]
[tex] 34,2 - 7,2 = n - 1[tex]
[tex] 27 = n - 1[tex]
[tex] 27 + 1 = n [tex]
[tex] n = 28 [tex]
Logo, a sala comportará 28 fileiras.
Portanto, alternativa "C".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
A luminosidade L de uma estrela está relacionada com o raio R e com a temperatura T dessa estrela segundo a Lei de Stefan-Boltzmann: [tex]L = c \cdot R^{2} \cdot T^{4}[tex], em que c é uma constante igual para todas as estrelas.
Disponível em: http://ciencia.hsw.uol.com.br. Acesso em: 22 nov. 2013 (adaptado).
Considere duas estrelas E e F, sendo que a estrela E tem metade do raio da estrela F e o dobro da temperatura de F.
Indique por [tex]L_{E}[tex] e [tex]L_{F}[tex] suas respectivas luminosidades.
A relação entre as luminosidades dessas duas estrelas é dada por
Como [tex]L = c \cdot R^{2} \cdot T^{4}[tex] e [tex]L_{E}[tex] a luminosidade da estrela E e [tex]L_{F}[tex] a luminosidade da estrela F.
Temos:
[tex]L_{E} = \frac{L_{F}}{2}[tex] e [tex]L_{E} = 2 \cdot L_{F}[tex]
Logo:
[tex] \frac{L_{E}}{L_{F}} = \frac{c\ \cdot\ (\frac{R_{F}}{2})^{2} \cdot\ (2\ T_{F})^{4}}{c\ \cdot\ R^{2}_{F}\ \cdot\ T^{4}_{F}} [tex]
[tex] \frac{L_{E}}{L_{F}} = \frac{c\ \cdot\ \frac{R_{F}^{2}}{4} \cdot\ 16\ T_{F}^{4}}{c\ \cdot\ R^{2}_{F}\ \cdot\ T^{4}_{F}} [tex]
[tex] \frac{L_{E}}{L_{F}} = 4[tex]
[tex] L_{E} = 4 \cdot L_{F}[tex]
Portanto, alternativa "D".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Uma das informações que pode auxiliar no dimensionamento do número de pediatras que devem atender em uma Unidade Básica de Saúde (UBS) é o número que representa a mediana da quantidade de crianças por família existente na região sob sua responsabilidade. O quadro mostra a distribuição das frequências do número de crianças por família na região de responsabilidade de uma UBS.
| Número de crianças por família | Frequência |
|---|---|
| 0 | 100 |
| 1 | 400 |
| 2 | 200 |
| 3 | 150 |
| 4 | 100 |
| 5 | 50 |
O número que representa a mediana da quantidade de crianças por família nessa região é
A soma das frequências é igual a 1000. Sendo:

Logo, a mediana é:
[tex]Me = \frac{1\ +\ 2}{2} = \frac{3}{2} = 1,5 [tex]
Portanto, alternativa "B".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Em jogos de voleibol, um saque é invalidado se a bola atingir o teto do ginásio onde ocorre o jogo. Um jogador de uma equipe tem um saque que atinge uma grande altura. Seu recorde foi quando a batida do saque se iniciou a uma altura de 1,5 m do piso da quadra, e a trajetória da bola foi descrita pela parábola [tex]y = - \frac{x^{2}}{6} - \frac{7x}{3} + 12 [tex], em que y representa a altura da bola em relação ao eixo x (das abscissas) que está localizado a 1,5 m do piso da quadra, como representado na figura. Suponha que em todas as partidas algum saque desse jogador atinja a mesma altura do seu recorde.

A equipe desse jogador participou de um torneio de voleibol no qual jogou cinco partidas, cada uma delas em um ginásio diferente. As alturas dos tetos desses ginásios, em relação aos pisos das quadras, são:
• ginásio I: 17 m;
• ginásio II: 18 m;
• ginásio III: 19 m;
• ginásio IV: 21 m;
• ginásio V: 40 m.
O saque desse atleta foi invalidado
A altura máxima descrita pela parábola [tex]y = - \frac{x^{2}}{6} - \frac{7x}{3} + 12 [tex] é a ordenada do vértice, que é dado por: [tex]y_{(vértice)} = \frac{-Δ}{4a} [tex]. Logo:
[tex]y_{(vértice)} = \frac{-Δ}{4a} [tex]
[tex]y_{(vértice)} = \frac{-(b^{2}\ -\ 4ac)}{4a} [tex]
[tex]y_{(vértice)} = \frac{-((\frac{-7}{3})^{2}\ -\ 4\ \cdot\ (\frac{-1}{6})\ \cdot\ 12)}{4\ \cdot\ (\frac{-1}{6})} [tex]
[tex]y_{(vértice)} = \frac{-(\frac{49}{9} + 8)}{\frac{-4}{6}} [tex]
[tex]y_{(vértice)} = \frac{-(\frac{49\ +\ 72}{9})}{\frac{-4}{6}} [tex]
[tex]y_{(vértice)} = \frac{\frac{121}{9}}{\frac{4}{6}} [tex]
[tex]y_{(vértice)} = \frac{121}{9} \cdot \frac{6}{4} [tex]
[tex]y_{(vértice)} = \frac{726}{36} = 20,16 [tex]
Assim, a altura do seu recorde é [tex]20,16 + 1,5 = 21,56\ m[tex].
= 20,16 + 1,5 = 21,56\ m[tex]
Portanto, o saque desse atleta foi invalidado nos ginásios I, II, III e IV.
Portanto, alternativa "D".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
O funcionário de uma loja tem seu salário mensal formado por uma parcela fixa de 675 reais mais uma comissão que depende da quantidade de peças vendidas por ele no mês. O cálculo do valor dessa comissão é feito de acordo com estes critérios:
• até a quinquagésima peça vendida, paga-se 5 reais por peça;
• a partir da quinquagésima primeira peça vendida, o valor pago é de 7 reais por peça. Represente por q a quantidade de peças vendidas no mês por esse funcionário, e por S(q) o seu salário mensal, em real, nesse mês.
A expressão algébrica que descreve S(q) em função de q é
Até a 50ª peça vendida, temos que a lei de formação é [tex]675 + 5q[tex], uma vez que há uma taxa fixa de 675 reais e cada peça custa 5 reais.
Ao vender mais de 50 peças, a loja fatura:
[tex]\underbrace{675}_{fixo} + \underbrace{50 \cdot 5}_{dinheiro\ arrecado\\ com\ as\ 50\\ primeiras\ vendas} + \underbrace{7(1 - 50)}_{há\ (q\ -\ 50)\ peças\\ que\ custam\\ 7 reais cada} [tex]
[tex]= 675 + 50 \cdot 5 + 7(q - 50) [tex]
[tex]= 675 + 250 + 7q - 350 [tex]
[tex]= 575 + 7q [tex]
Dessa, forma a resposta é:
[tex] S(q) = \begin{cases} 675 + 5q,\ se\ q\ ≤\ 50 \\ 575 + 7q,\ se\ q\ >\ 50 \end{cases} [tex]
Portanto, alternativa "E".
(Créditos da resolução: Equipe Descomplica).
(ENEM 2022 - 1ª Aplicação).
Ao analisar os dados de uma epidemia em uma cidade, peritos obtiveram um modelo que avalia a quantidade de pessoas infectadas a cada mês, ao longo de um ano. O modelo é dado por [tex]p(t) = -t^{2} + 10t + 24 [tex], sendo t um número natural, variando de 1 a 12, que representa os meses do ano, e a quantidade de pessoas infectadas no mês t do ano. Para tentar diminuir o número de infectados no próximo ano, a Secretaria Municipal de Saúde decidiu intensificar a propaganda oficial sobre os cuidados com a epidemia. Foram apresentadas cinco propostas (I, II, III, IV e V), com diferentes períodos de intensificação das propagandas:
• I: 1 ≤ t ≤ 2;
• II: 3 ≤ t ≤ 4;
• III: 5 ≤ t ≤ 6;
• IV: 7 ≤ t ≤ 9;
• V: 10 ≤ t ≤ 12.
A sugestão dos peritos é que seja escolhida a proposta cujo período de intensificação da propaganda englobe o mês em que, segundo o modelo, há a maior quantidade de infectados. A sugestão foi aceita.
A proposta escolhida foi a
Por se tratar de uma função quadrática, o x vértice representa o mês com maior número de infectados. Logo:
[tex]t_{(vértice)} = \frac{-b}{2a} = \frac{-10}{2\ \cdot\ (-1)} = \frac{-10}{- 2} = 5 [tex]
Portanto a proposta escolhida deverá ser a III.
Portanto, alternativa "C".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Um atleta iniciou seu treinamento visando as competições de fim de ano. Seu treinamento consiste em cinco tipos diferentes de treinos: treino [tex]T_{1}[tex], treino [tex]T_{2}[tex], treino [tex]T_{3}[tex], treino [tex]T_{4}[tex] e treino [tex]T_{5}[tex]. A sequência dos treinamentos deve seguir esta ordem:

A letra R significa repouso. Após completar a sequência de treinamentos, o atleta começa novamente a sequência a partir do treino [tex]T_{1}[tex] e segue a ordem descrita. Após 24 semanas completas de treinamento, se dará o início das competições.
A sequência de treinamentos que o atleta realizará na 24ª semana de treinos é
Em 24 semanas, temos 24 ∙ 7 = 168 dias. Repetindo a sequência dos treinamentos, temos:

Nos últimos 7 dias, a sequência de treinamento é a dos dias 162 a 168, ou seja, R T3 R T4 R R T5.
Portanto, alternativa "B".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Um robô, que tem um ímã em sua base, se desloca sobre a superfície externa de um cubo metálico, ao longo de segmentos de reta cujas extremidades são pontos médios de arestas e centros de faces. Ele inicia seu deslocamento no ponto P, centro da face superior do cubo, segue para o centro da próxima face, converte à esquerda e segue para o centro da face seguinte, converte à direita e continua sua movimentação, sempre alternando entre conversões à esquerda e à direita quando alcança o centro de uma face. O robô só termina sua movimentação quando retorna ao ponto P. A figura apresenta os deslocamentos iniciais desse robô.

A projeção ortogonal do trajeto descrito por esse robô sobre o plano da base, após terminada sua movimentação, visualizada da posição em que se está enxergando esse cubo, é
Continuando a trajetória do robô, temos a seguinte figura:

A projeção ortogonal do trajeto descrito pelo robô é indicado em vermelho na figura.
Portanto, alternativa "A".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Uma empresa de engenharia projetou uma casa com a forma de um retângulo para um de seus clientes. Esse cliente solicitou a inclusão de uma varanda em forma de L. A figura apresenta a planta baixa desenhada pela empresa, já com a varanda incluída, cujas medidas, indicadas em centímetro, representam os valores das dimensões da varanda na escala de 1 : 50.

A medida real da área da varanda, em metro quadrado, é
Observe a figura a seguir:

A área [tex]S’[tex] da varanda é dada pela soma dos retângulos [tex]ABCD[tex] e [tex]DEFG[tex], deu:
[tex] S’ = 16 \cdot 5 + 4 \cdot 13,4 [tex]
[tex] S’ = 80 + 53,6 = 133,6\ cm^{2} [tex]
Chamando de [tex]S[tex] a área real da varanda, temos que:
[tex] \frac{S’}{S} = (\frac{1}{50})^{2} [tex]
[tex] \frac{133,6}{S} = \frac{1}{2\ 500} [tex]
[tex] S = 133,6 \cdot 2\ 500 [tex]
[tex] S = 334\ 000\ cm^{2} = 33,40\ m^{2} [tex]
Portanto, alternativa "A".
(Créditos da resolução: Curso Objetivo)
(ENEM 2022 - 1ª Aplicação).
Uma loja de roupas fixou uma meta de vendas de 77 000 reais para um determinado mês de 30 dias. O gráfico mostra o volume de vendas dessa loja, em real, nos dez primeiros dias do mês e entre o dia dez e o dia vinte desse mês, nos seus dois únicos setores (infantil e adulto). Suponha que a variação no volume de vendas, para o período registrado, tenha se dado de forma linear, como mostrado no gráfico, e que essa tendência se mantenha a mesma para os próximos dez dias.

Ao final do trigésimo dia, quanto faltará no volume de vendas, em real, para que a meta fixada para o mês seja alcançada?
Mantidas as tendências para os próximos dez dias, o volume de vendas dos setores adultos e infantil serão, respectivamente, 12 000 e 6 000 reais.
Assim, o volume de vendas, por setor é:
Adulto: 18 000 + 15 000 + 12 000 = 45 000 reais
Infantil: 8 000 + 7 000 + 6 000 = 21 000 reais
Total: 45 000 + 21 000 = 66 000 reais.
Para alcançar a meta de 77 000 reais faltam 11 000 reais.
Portanto, alternativa "C".
(Créditos da resolução: Curso Objetivo)
