(ENEM 2023 - 2ª Aplicação - PPL).
No ano em que uma empresa lançou seu novo modelo de celular no mercado brasileiro, investiu 45 milhões de reais no primeiro semestre em cada uma das cinco regiões do país, colocando à venda 30 mil aparelhos por região. No primeiro semestre, todos os aparelhos colocados à venda foram vendidos, gerando um lucro total de 30 milhões de reais. No segundo semestre, a empresa decidiu que faria o mesmo investimento e colocou à venda as mesmas quantidades de aparelhos por região. Por causa da demanda observada, a empresa considerou que todos os aparelhos desse modelo que fossem ofertados sejam vendidos e, além disso, planeja obter um lucro total 10% maior no segundo semestre do que o que obteve no primeiro.
Para que essa empresa alcance o lucro planejado, qual deve ser o valor de venda, em real, de um aparelho celular desse modelo, no segundo semestre desse ano?
Cálculo do total de investimento nas 5 regiões;
[tex] = R \$\ 45 000\ 000 \cdot 5 = R \$\ 22\ 000\ 000 [tex]
Como planeja obter um lucro de 10% (100% + 10% = 110% = 1,1) maior no segundo semestre, logo:
[tex] = R \$\ 30\ 000\ 000 \cdot 110 \% [tex]
[tex] = R \$\ 30\ 000\ 000 \cdot 1,1 [tex]
[tex] = R \$\ 33\ 000\ 000 [tex]
Para alcançar o lucro planejado, o valor de venda, em real, de um aparelho celular desse modelo, no segundo semestre desse ano é:
[tex]= \frac{Total\ (gasto\ +\ lucro)}{Quantidade\ de\ celulares} [tex]
[tex]= \frac{R \$\ 225\ 000\ 000\ +\ R \$\ 33\ 000\ 000}{150\ 000} [tex]
[tex]= \frac{R \$\ 258\ 00\color{Red}{0\ 000}}{15\color{Red}{0\ 000}} [tex]
[tex]= \frac{R \$\ 25\ 800}{15} [tex]
[tex]= R \$\ 1\ 720,00 [tex]
Portanto, Alternativa "B".
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
A amplitude é uma medida estatística que detecta a variabilidade dos dados de uma amostra. Ela pode ser utilizada como critério de qualidade da produção na indústria de peças, indicando, por exemplo, a necessidade do descarte de um lote defeituoso. Uma fábrica analisou cinco unidades de cada um dos cinco lotes da produção de um tipo de peça que, por projeto, devem ter comprimento igual a 10 cm. As medidas, em centímetro, dessas unidades estão distribuídas a seguir:
• lote I: 9,80; 10,30; 10,30; 10,30 e 10,30;
• lote II: 10,55; 10,58; 10,58; 10,60 e 10,60;
• lote III: 9,80; 9,80; 10,00; 10,00 e 10,20;
• lote IV: 9,90; 9,90; 9,90; 10,20 e 10,20;
• lote V: 9,30; 9,30; 9,50; 9,50 e 9,50.
Foi determinado o descarte do lote que apresentasse a maior amplitude.
De acordo com o critério adotado, a fábrica descartará o lote
Calcular a amplitude de cada lote, sabendo que a amplitude é a diferença entre o maior e o menor comprimento.
• [tex]Lote\ I:\ = 10,30 - 9,80 = \color{Red}{0,5\ cm } [tex]
• [tex]Lote\ II:\ = 10,60 - 10,55 = 0,05\ cm [tex]
• [tex]Lote\ III:\ = 10,20 - 9,80 = 0,4\ cm [tex]
• [tex]Lote\ IV:\ = 10,20 - 9,90 = 0,3\ cm [tex]
• [tex]Lote\ V:\ = 9,50 - 9,30 = 0,2\ cm [tex]
O descarte ser o lote I.
Portanto, alternativa "A".
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Em um ateliê de costura, para confeccionar 200 calças jeans, em 5 dias de trabalho, são necessários 10 funcionários. Devido a uma crise financeira no ateliê, a gerência decidiu demitir 4 funcionários visando a redução de custos. Sabe-se que a produção deverá ser mantida com o novo quadro de funcionários, ou seja, após a demissão.
Em quantos dias de trabalho o novo quadro de funcionários confeccionará a mesma quantidade de calças jeans?
A quantidade dias de trabalho no novo quadro de funcionários:
Calças dias funcionários
[tex] \color{Red}{200} 5 10 [tex]
[tex] \color{Red}{200} x 10\ –\ 4 = 6 [tex]
Como as grandezas dias e funcionários são inversamente proporcionais. Logo:
[tex] 5 6 [tex]
[tex] x 10 [tex]
[tex] 6x = 5 \cdot 10 [tex]
[tex] x = \frac{50}{6} [tex]
[tex] x \cong 8,33\ dias [tex]
Portanto, alternativa "D".
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
No espaço, a falta de gravidade faz com que o organismo produza mais cálcio e, como o mineral não é usado, o corpo o expele, fazendo com que os ossos diminuam de tamanho. Um dos ossos que sofrem essa redução é o fêmur. O gráfico apresenta a evolução linear do tamanho desse osso, ao longo de três meses, em um astronauta que, antes de ir para o espaço, tinha um fêmur de 50 cm.

DUARTE, M. O guia dos curiosos. São Paulo: Panda Books, 2015 (adaptado).
Como esse astronauta ficará cinco meses no espaço, considere que a tendência de sua evolução óssea, observada nos três primeiros meses, mantenha-se a mesma ao longo dos próximos meses.
O tamanho, em centímetro, do fêmur desse astronauta, ao completar quatro meses no espaço, será
Como o gráfico apresenta a evolução linear do tamanho desse osso, logo:
[tex]\frac{50\ cm}{0\ mês} = \frac{48,5\ cm}{2\ meses} = \frac{x\ cm}{4\ meses}[tex]
[tex]\frac{48,5\ -\ 50}{2\ -\ 0} = \frac{x\ -\ 48,5}{4\ -\ 2} [tex]
[tex]\frac{-\ 1,5}{\color{Red}{2}} = \frac{x\ -\ 48,5}{\color{Red}{2}} [tex]
[tex]-\ 1,5x = x\ -\ 48,5 [tex]
[tex]-\ 1,5x + 48,5 = x[tex]
[tex] x = 47,0[tex]
Portanto, alternativa (D).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Uma pessoa tinha um projeto para um salão de festas no formato de paralelepípedo reto retângulo. Ela comprou a quantidade exata de azulejos para cobrir as paredes laterais, incluindo as regiões destinadas a uma porta e uma janela. Os azulejos que cobririam essas regiões seriam reservados para futuras substituições. Esse projeto previa que o salão teria, como dimensões internas, 10 m de comprimento por 6 m de largura por 2,5 m de altura. Em decorrência de uma mudança no projeto, o salão ficará com 12 m de comprimento por 5 m de largura e as mesmas dimensões para porta e janela. Como a compra de azulejos já foi feita, essa pessoa ajustará a altura do salão de modo que a área lateral, incluindo as regiões da porta e da janela, seja equivalente à área lateral antes da alteração do projeto.
Qual é a medida, em metro, dessa nova altura, expressa com duas casas decimais?
Primeiro encontrar a área das paredes do projeto inicial:

[tex] Área = 2 \cdot 2,5 \cdot 6 + 2 \cdot 10 \cdot 2,5 [tex]
[tex] Área = 30 + 50 [tex]
[tex] Área = 80\ m^{2}[tex]
Agora, encontrar a área das paredes do projeto alterado:

[tex] Área = 2 \cdot h \cdot 5 + 2 \cdot 12 \cdot h [tex]
[tex] Área = 10h + 24h [tex]
[tex] Área = 34h\ m^{2}[tex]
Como o novo projeto terá área equivalente à área lateral antes da alteração do projeto. Logo, a altura será:
[tex]34h = 80 [tex]
[tex]h = \frac{80}{34} [tex]
[tex]h = 2,35\ m [tex]
Portanto, alternativa (D).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
A trajetória de um avião durante um voo entre duas cidades ocorre dentro de áreas de controle de tráfego. Durante um voo, é exigido que o avião sobrevoe pontos de controle situados no solo e demarcados entre a origem (O) e o destino (D) da aeronave. Assim, embora a trajetória do avião ocorra num espaço tridimensional, para o controlador de voo, a visualização representativa dessa trajetória é dada por uma linha poligonal plana, em que três pontos de controle sucessivos, nas representações, devem ser não colineares.
Disponível em: www.kaspersky.com.br. Acesso em: 21 out. 2019 (adaptado).
As figuras apresentam algumas possibilidades dessas representações, nas quais todos os pontos de controle estão representados.

Suponha que um avião fez um voo com origem diferente do destino final e cuja representação apresente três pontos de controle.
Nesse voo, qual das figuras apresentadas é compatível com as restrições estabelecidas?
A figura compatível com as restrições estabelecidas é a I, é a única que apresenta por uma linha poligonal plana, em que três pontos de controle sucessivos, nas representações, devem ser não colineares.

Portanto, alternativa (A).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
O Torcidômetro é uma ferramenta para se entender a dinâmica do crescimento ou encolhimento das torcidas dos times de futebol no país. O gráfico mostra a variação percentual, entre 1993 e 2007, das torcidas de cinco times numerados em: I, II, III, IV e V.

Disponível em: www.netvasco.com.br. Acesso em: 25 fev. 2009.
Os dados exibidos no gráfico indicam que a torcida que apenas cresceu, entre fevereiro de 2006 e agosto de 2007, foi a torcida do time
Fazendo uma leitura direta do gráfico constatamos que a torcida que apenas cresceu entre fevereiro de 2006 e agosto de 2007, foi a torcida do time IV.

Portanto, alternativa (D).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Um tipo de célula se reproduz constantemente por divisão celular, triplicando sua quantidade a cada duas horas, sob condições ideais de proliferação. Suponha uma quantidade inicial [tex]Q_{0}[tex] dessas células sob as condições ideais de proliferação durante um certo período.
Qual a representação algébrica da quantidade Q dessas células em função do tempo [tex]t[tex], em hora, nesse período?
Encontrar a expressão exponencial da quantidade Q dessas células em função do tempo t, em hora, nesse período, sabendo que nessa divisão, triplica a quantidade de células a cada duas horas:
[tex]Q_{t} = Q_{0} \cdot 3^{kt}[tex]
[tex]3 \cdot \color{Red}{Q_{0}} = \color{Red}{Q_{0}} \cdot 3^{kt}[tex]
[tex]3 = 3^{k \cdot 2}[tex]
[tex]3^{1} = 3^{2k}[tex]
Logo:
[tex]1 = 2k[tex]
[tex]\frac{1}{2} = k[tex]
Agora, substituir o valo de k na expressão:
[tex]Q_{t} = Q_{0} \cdot 3^{kt}[tex]
[tex]Q_{t} = Q_{0} \cdot 3^{\frac{t}{2}}[tex]
Portanto, alternativa (D).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
A proprietária de uma confecção pretende liquidar as camisas que possui em estoque, por meio de uma promoção na qual fará a venda de lotes com iguais quantidades de camisas. Para a 1ª semana, pretende anunciar a venda de cada lote de camisas por R$ 720,00. Na 2ª semana, para acelerar as vendas, planeja anunciar a venda de lotes com 3 unidades a mais do que os lotes vendidos na primeira semana, ainda por R$ 720,00 cada lote, e de forma que o preço unitário de cada peça seja R$ 20,00 mais baixo do que o valor que teria sido cobrado por peça na 1ª semana de promoção.
Quantas camisas deverão conter os lotes que serão colocados à venda na 1ª semana para que seja possível praticar essa promoção?
Equacionando o problema:
Quantidade de camisetas por lote: [tex]x [tex]
Preço de cada camiseta: [tex]y [tex]
Logo, temos:
[tex] \begin{cases} \frac{720}{x} = y \Longrightarrow 720 = xy (I) \\ \\ \frac{720}{x + 3} = y - 20 (II)\end{cases} [tex]
Desenvolvendo a equação II, temos:
[tex] \frac{720}{x + 3} = y - 20 [tex]
[tex] 720 = (x + 3)(y - 20) [tex]
[tex] 720 = xy - 20x + 3y - 60 [tex]
Substituindo [tex] 720 = xy [tex], da equação (I).
[tex] 720 = 720 -\ 20x + 3y - 60 [tex]
[tex] 720 - 720 = -\ 20x + 3y - 60 [tex]
[tex] 0 = -\ 20x + 3y - 60 [tex] (III)
Agora, substituir novamente a equação (I) em (III).
[tex] 0 = -\ 20x + 3y - 60 [tex]
[tex] 0 = -\ 20x + 3 \cdot \frac{720}{x} - 60 [tex]
[tex] 0 = -\ 20x + \frac{2\ 160}{x} - 60 (÷\ 20) [tex]
[tex] 0 = -\ x + \frac{108}{x} - 3 (×\ x) [tex]
[tex] 0 = -\ x^{2} + 108 - 3x [tex]
[tex] 0 = -\ x^{2} - 3x + 108 [tex]
Agora, resolver a equação do segundo grau:
[tex]a = -\ 1; b = -\ 3 [tex] e [tex] c = 108 [tex]
[tex] Δ = b^{2} - 4ac = (-3)^{2} - 4 \cdot (-1) \cdot 108 = 9 + 432 = 441 [tex]
[tex] x = \frac{-b\ \pm\ \sqrt{Δ}}{2a} = \frac{-\ (-\ 3)\ \pm\ \sqrt{441}}{2\ \cdot\ (-1)} = \frac{3\ \pm\ {21}}{-2} [tex]
[tex] x' = \frac{3\ +\ {21}}{-2} = \frac{24}{-\ 2} = -\ 12 (não\ convém!) [tex]
e
[tex] x'' = \frac{3\ -\ {21}}{-\ 2} = \frac{-\ 18}{-\ 2} = 9 [tex]
Portanto, alternativa (A).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Um rolo de papel higiênico tradicional é representado por um cilindro circular reto retirando-se outro cilindro circular reto interior, de mesmo eixo de simetria, mesma altura e diâmetro menor, conforme a figura.

Considere um rolo de papel higiênico com 12 cm de diâmetro externo, 4 cm de diâmetro interno e 10 cm de altura.
O volume, em centímetro cúbico, desse rolo é
O volume, em centímetro cúbico, desse rolo é
[tex]Volume = πR^{2}H\ -\ πr^{2}h [tex]
[tex]Volume = π \cdot 6^{2} \cdot 10\ -\ π \cdot 2^{2} \cdot 10 [tex]
[tex]Volume = π \cdot 36 \cdot 10\ -\ π \cdot 4 \cdot 10 [tex]
[tex]Volume = 360π -\ 40π [tex]
[tex]Volume = 320π\ cm^{2} [tex]
Portanto, alternativa (C).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Para o tratamento de uma doença específica, existem disponíveis no mercado somente quatro medicamentos, que são comercializados em versões diferentes.
• Medicamento I: caixa com 25 comprimidos, com preço de R$ 50,00.
• Medicamento II: caixa com 30 comprimidos, com preço de R$ 48,00.
• Medicamento III: caixa com 40 comprimidos, com preço de R$ 60,00.
• Medicamento IV: caixa com 60 comprimidos, com preço de R$ 100,00.
Um laboratório lançou um novo medicamento, chamado Z, para o tratamento dessa doença. Visando tornar esse medicamento competitivo economicamente, o laboratório decidiu fixar um preço que apresente o menor valor por comprimido em relação aos medicamentos já existentes.
O preço máximo, por comprimido, do medicamento Z será
Cálculo do preço de cada comprimido de cada medicamento:
• [tex]Medicamento\ I: \frac{R \$\ 50,00}{25\ comprimidos} = R \$\ 2,00 [tex]
• [tex]Medicamento\ II: \frac{R \$\ 48,00}{30\ comprimidos} = R \$\ 1,60 [tex]
• [tex]Medicamento\ III: \frac{R \$\ 60,00}{40\ comprimidos} = R \$\ 1,50 [tex]
• [tex]Medicamento\ IV: \frac{R \$\ 100,00}{60\ comprimidos} = R \$\ 1,66 [tex]
Logo, o medicamento Z, deve ser vendido com preço no máximo R$ 1,59 para ter o menor valor por comprimido em relação aos medicamentos já existentes.
Portanto, alternativa (B).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Uma costureira tem à sua disposição pelo menos duas unidades de cada um dos quatro tipos de retalhos retangulares com as estampas e os tamanhos apresentados.

Para confeccionar um tapete em formato retangular de 10 cm × 50 cm, ela utilizará os retalhos, na posição indicada na figura, costurando um lado de um a um lado do outro, sem que haja rotações desses retalhos. O modelo de tapete que pretende confeccionar deverá conter um único retalho de 10 cm × 20 cm e mais três retalhos de formato 10 cm × 10 cm, sendo que retalhos de mesma estampa não poderão ficar lado a lado.
Quantos modelos diferentes de tapetes poderão ser confeccionados?
Primeiro encontrar a quantidade de possibilidades com 4 retalhos:
[tex] P! = 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24\ tapetes[tex]
Agora, com o máximo de tapetes com 2 pedaços iguais, sabendo que deve conter um único retalho de 10 cm × 20 cm, sendo que retalhos de mesma estampa não poderão ficar lado a lado. Logo:
[tex] 3 \cdot P_{4}^{2} = 3 \cdot \frac{4!}{2!} = 3 \cdot \frac{4\ \cdot\ 3\ \cdot \ \color{Red}{2!}}{\color{Red}{2!}} = 3 \cdot 12 = 36[tex]
Logo, temos um total de:
[tex]= 24 + 36 [tex]
[tex]= 60\ tapetes [tex]
Portanto, alternativa (E).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Restaurantes geralmente se deparam com o problema de definir a quantidade de alimentos a serem preparados para cada dia. Diante desse problema, o gerente de um restaurante anotou as quantidades de clientes que almoçaram em seu restaurante durante os 10 primeiros dias do mês e registrou esses dados, obtendo este gráfico:

Ele considerou a moda da distribuição das quantidades de clientes que almoçaram em seu restaurante nesses 10 primeiros dias do mês como uma boa medida para dimensionar a quantidade de alimentos a serem preparados diariamente.
O valor da moda dessa distribuição é
A moda é a variável que mais repete. Logo, 94 repetiu 3 vezes.
Portanto, alternativa (D).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Um estudante de arquitetura projetou um prédio de 32 m de altura a ser construído em uma maquete, em papel-cartão, na escala 1 : 50.
Nesse caso, na maquete, a altura do prédio mede
Como uma escala é uma grandeza diretamente proporcional, logo:
[tex] Maquete prédio [tex]
[tex] 1\ cm 50\ cm = 0,5 m [tex]
[tex] x\ cm 32\ m [tex]
[tex] 0,5x = 32 [tex]
[tex] x = \frac{32}{0,5} [tex]
[tex] x = 64\ cm [tex] ou [tex] 0,64\ m [tex]
Portanto, alternativa (C).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Um reservatório que abastece uma região urbana está com uma quantidade V de água. Previsões meteorológicas indicam que a região passará por uma escassez de chuva e, por isso, as autoridades locais determinaram a realização de várias medições do volume de água nesse reservatório para efeito de monitoramento.
A primeira medição indicou que o volume de água reduziu-se à metade; a segunda indicou a retirada da terça parte do que restou; a terceira, a retirada da quarta parte do que restou; a quarta, a retirada da quinta parte do que restou e assim sucessivamente nas demais medições, mantendo o seguinte padrão de retirada: na n-ésima medição, a retirada da (n + 1)-ésima parte do que restou.
Considere que não houve reabastecimento de água no reservatório no período em que foram feitas as medições.
Mantendo esse padrão de retirada, as quantidades de água restantes no reservatório referentes às 7ª, 8ª e 9ª medições são iguais a, respectivamente,
Observe a sequências de medições de água do reservatório:
1ª medição: [tex] \frac{V}{2}[tex]
2ª medição: Se retirou [tex] \frac{1}{3}[tex] então deve sobrar [tex]\frac{2}{3}[tex]. Logo, [tex] \frac{V}{\color{Red}{2}} \cdot \frac{\color{Red}{2}}{3} = \frac{V}{3}[tex].
3ª medição: Se retirou [tex] \frac{1}{4}[tex] então deve sobrar [tex]\frac{3}{4}[tex]. Logo, [tex] \frac{V}{\color{Red}{3}} \cdot \frac{\color{Red}{3}}{4} = \frac{V}{4}[tex].
4ª medição: Se retirou [tex] \frac{1}{5}[tex] então deve sobrar [tex]\frac{4}{5}[tex]. Logo, [tex] \frac{V}{\color{Red}{4}} \cdot \frac{\color{Red}{4}}{5} = \frac{V}{5}[tex].
... (Existe um padrão de repetição)
5ª medição: [tex] = \frac{V}{6}[tex].
6ª medição: [tex] = \frac{V}{7}[tex].
7ª medição: [tex] = \frac{V}{8}[tex].
8ª medição: [tex] = \frac{V}{9}[tex].
9ª medição: [tex] = \frac{V}{10}[tex].
Portanto, alternativa (E).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Um equipamento monitora o volume de água que passa por uma tubulação em um período de tempo. Um técnico rascunhou cinco possibilidades de unidade de medida para a grandeza que esse equipamento monitora.
Nas imagens, [tex]cm[tex] significa centímetro, e [tex]s[tex] significa segundo.

O rascunho que expressa corretamente uma unidade de medida para a grandeza que esse equipamento monitora é o
O volume de água que passa é dado por:
[tex] Vazão = \frac{Volume}{tempo} = \frac{m^{3}}{s} [tex]
Portanto, alternativa (C).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Uma pessoa comprou uma caixa com 25 bombons por 5 reais. Resolveu revendê-los de forma avulsa a um preço único. Não resistindo à tentação, durante a venda, comeu cinco bombons. Obteve, mesmo assim, com a venda dos bombons restantes, um lucro de 20% sobre o valor pago pela caixa.
Qual foi o valor, em real, de venda de cada bombom?
Essa pessoa tinha 25 bombons, comeu 5, restou 20.
Valor da arrecadação:
[tex] = R \$\ 5,00 + 20 \%\ de\ lucro [tex]
[tex] = R \$\ 5,00 + 0,2\ de\ R \$\ 5,00 [tex]
[tex] = R \$\ 5,00 + R \$\ 1,00 [tex]
[tex] = R \$\ 6,00 [tex]
Agora, encontrar o preço de cada bombom:
[tex] = \frac{R \$\ 6,00}{20\ bombons} = R \$\ 0,30[tex]
Portanto, alternativa (C).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Especialistas do Instituto Internacional de Águas de Estocolmo estimam que cada pessoa necessita de, no mínimo, 1 000 m3 de água por ano, para consumo, higiene e cultivo de alimentos. Sabe-se também que o Rio Amazonas despeja 200 000 m3 de água no mar por segundo.
Scientific America Brasil, set. 2008.
Por quanto tempo deveríamos coletar as águas que o Rio Amazonas despeja no mar para manter a população da cidade de São Paulo, estimada em 20 milhões de pessoas, por um ano?
Observe que o consumo de água da população de São Paulo é de:
[tex]= 20\ milhões \cdot 1\ 000\ m^{3} [tex]
[tex]= 20\ 000\ 000 \cdot 1\ 000\ m^{3} [tex]
[tex]= 2 \cdot 10^{10}\ m^{3}[tex]
Agora, o tempo necessário é:
[tex] 200\ 000\ m^{3} = 2 \cdot 10^{5}\ m^{3} -----\ 1\ segundo [tex]
[tex] 2 \cdot 10^{10}\ m^{3} -----\ x\ segundo [tex]
[tex] 2\ \cdot\ 10^{5}x = 2 \cdot 10^{10} [tex]
[tex] x = \frac{2\ \cdot\ 10^{10}}{2\ \cdot\ 10^{5}} [tex]
[tex] x = 10^{5} = 100\ 000\ segundos [tex]
Agora, fazer a conversão:
[tex] = 100\ 000\ s = 1\ 666,66...\ minutos = 27,77 ... horas [tex]
[tex] = 1\ dia,\ 3\ horas,\ 46\ minutos\ e\ 40\ segundos [tex]
Portanto, alternativa (C).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Mariana não tem computador pessoal em casa e precisa fazer uma pesquisa na internet para um trabalho de escola. Então, foi até uma lan house perto de sua casa. Na porta da lan house havia esta placa:
| ACESSO À INTERNET R$ 0,12 POR MINUTOS R$ 2,00 (TAXA DE UTILIZAÇÃO) |
|---|
Assim, quantos reais Mariana pagaria para ficar uma hora e meia usando a internet nessa lan house?
O valor gasto por Mariana por uma hora e meia (90 minutos) nesta na lan house foi de:
[tex] V = 2,00 + 0,12 \cdot t [tex]
[tex] V = 2,00 + 0,12 \cdot 90 [tex]
[tex] V = 2,00 + 10,80[tex]
[tex] V = 12,80[tex]
Portanto, alternativa (E).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Uma padaria criou uma receita de bolo chamada Bolo de xícara, pois, com exceção dos ovos e do fermento, os demais ingredientes são medidos com xícaras de mesma capacidade, conforme descrito.

O modo de fazer a receita orienta colocar, primeiramente, os ovos e depois ir adicionando os ingredientes cujas quantidades foram medidas em xícara, da menor para a maior quantidade. Por último, adiciona-se o fermento.
Em qual ordem os ingredientes medidos em xícara serão adicionados na receita?
Observe as conversões:
• Farinha de trigo: [tex] \frac{9}{4} = 2,25\ xícaras [tex]
• Chocolate em pó: [tex] \frac{4}{3} = 1,33...\ xícara [tex]
• Açúcar: [tex] 1\frac{3}{4} = 1,75\ xícara [tex]
• Leite: [tex] \frac{5}{6} = 0,8333...\ xícara [tex]
Agora, é ordenar da menor para a maior quantidade:
[tex]\frac{5}{6} < \frac{4}{3} < 1 \frac{3}{4} ; < \frac{9}{4} [tex]
[tex]Leite\ <\ chocolate\ <\ açúcar\ <\ farinha\ de\ trigo [tex]
Portanto, alternativa (B).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Em um pronto-socorro, um paciente ingeriu, à meia-noite, um comprimido que continha 800 mg de uma medicação. O médico, ao liberar o paciente, informou que, caso ele voltasse a sentir dores, deveria tomar outro comprimido daquele, no máximo três vezes, nas próximas 24 horas, dependendo das recomendações da bula. Como o paciente voltou a sentir dores ao chegar em casa, ainda na madrugada, decidiu seguir a orientação do médico e leu a bula do remédio. O paciente verificou que, a cada 6 horas, a quantidade dessa medicação no organismo se reduzia à metade da quantidade anterior. Observou também a recomendação de que a pessoa deveria, preferencialmente, ingerir um novo comprimido quando a quantidade de medicação no organismo estivesse compreendida entre 200 mg e 100 mg.
Seguindo as informações e recomendações da bula, em que período(s) do dia o paciente deveria tomar novamente o remédio?
Como a cada 6 horas, a quantidade dessa medicação no organismo se reduzia à metade da quantidade anterior, ou seja, a meia-vida é de 6 horas. Também, ele tomou o primeiro comprimento à meia-noite. E deverá ingerir um novo comprimido quando a quantidade de medicação no organismo estivesse compreendida entre 200 mg e 100 mg. Logo:
[tex]00h \Longrightarrow 800\ mg [tex]
[tex]06h \Longrightarrow 400\ mg [tex]
[tex]12h \Longrightarrow 200\ mg [tex]
[tex]18h \Longrightarrow 100\ mg [tex]
Considerando que às 12h já começa à tarde. Então, o paciente deverá tomar novamente o comprimento no período vespertino.
Portanto, alternativa (D).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Uma pessoa, procurando um estacionamento, encontrou cinco opções com as seguintes formas de cobrança:
• A: R$ 6,00 por hora ou fração de hora;
• B: R$ 6,00 pelas duas primeiras horas e R$ 3,00 a cada hora ou fração de hora subsequente;
• C: R$ 6,00 por hora ou fração de hora, com tolerância de 15 minutos;
• D: R$ 6,00 pelas duas primeiras horas e R$ 3,00 a cada hora ou fração de hora subsequente, com tolerância de 15 minutos;
• E: R$ 0,10 por minuto.
Essa pessoa irá utilizar o estacionamento por 5 horas e 12 minutos.
O estacionamento que permite a essa pessoa pagar o menor valor possível é
Encontrar o estacionamento que permite que essa pessoa pague o menor valor possível, sabendo que ela irá utilizar o estacionamento por 5 horas e 12 minutos.
Estacionamento A:
[tex]= 5\ horas + 12\ minutos [tex]
[tex]= 5 \cdot R \$\ 6,00 + R \$\ 6,00 [tex]
[tex]= R \$\ 36,00 [tex]
Estacionamento B:
[tex]= 5\ horas + 12\ minutos [tex]
[tex]= 2 \cdot R \$\ 6,00 + 3 \cdot R \$\ 3,00 + R \$\ 3,00[tex]
[tex]= R \$\ 24,00 [tex]
Estacionamento C:
[tex]= 5\ horas + 12\ minutos [tex]
[tex]= 5 \cdot R \$\ 6,00 [tex]
[tex]= R \$\ 30,00 [tex]
Estacionamento D:
[tex]= 5\ horas + 12\ minutos [tex]
[tex]= 2 \cdot R \$\ 6,00 + 3 \cdot R \$\ 3,00[tex]
[tex]= \color{Red}{R \$\ 21,00}[tex]
Estacionamento E:
[tex]= 5\ horas + 12\ minutos [tex]
[tex]= 5 \cdot 60 + 12 = 312\ min [tex]
[tex]= 312 \cdot R \$\ 0,10 [tex]
[tex]= R \$\ 31,20 [tex]
Logo, o estacionamento que permite a essa pessoa pagar o menor valor possível é D.
Portanto, alternativa (D).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Estudantes de psicologia experimental estão analisando um modelo matemático que foi desenvolvido a partir de um experimento com pombos. Nesse experimento, um alimento considerado como uma recompensa reforçadora era fornecido em quantidades ([tex]Q[tex]) para as aves, com a possibilidade de atraso no tempo de entrega.
O modelo matemático que relaciona os valores reforçadores [tex]V_{1}[tex] e [tex]V_{2}[tex] de duas recompensas em função de suas respectivas quantidades [tex]Q_{1}[tex] e [tex]Q_{2}[tex] e de seus respectivos tempos de atraso [tex]T_{1}[tex] e [tex]T_{2}[tex] na disponibilização de cada uma delas é
[tex] \frac{V_{1}}{V_{2}} = \frac{Q_{1}}{Q_{2}} \cdot \frac{T_{1}}{T_{2}} [tex]
Ao analisarem o caso em que a quantidade [tex]Q_{1}[tex] é o dobro da quantidade [tex]Q_{2}[tex], cinco estudantes fizeram as seguintes afirmações sobre em que condição o valor [tex]V_{1}[tex] será maior que o valor [tex]V_{2}[tex]:
• estudante 1: sempre, pois [tex]Q_{1}[tex] é o dobro de [tex]Q_{2}[tex];
• estudante 2: apenas quando a razão entre [tex]T_{2}[tex] e [tex]T_{1}[tex] for maior que 0,5;
• estudante 3: apenas quando a razão entre [tex]T_{2}[tex] e [tex]T_{1}[tex] for menor que 0,5;
• estudante 4: apenas quando [tex]T_{1}[tex] for igual a [tex]T_{2}[tex];
• estudante 5: apenas quando a razão entre [tex]T_{2}[tex] e [tex]T_{1}[tex] for maior que 0,5 e menor que 1.
Qual estudante fez a afirmação correta?
Como a quantidade [tex]Q_{1}[tex] é o dobro da quantidade [tex]Q_{2}[tex], ou seja, [tex]Q_{1} = 2 Q_{2}[tex], logo devemos ter:
[tex] \frac{V_{1}}{V_{2}} = \frac{Q_{1}}{Q_{2}} \cdot \frac{T_{1}}{T_{2}} [tex]
[tex] \frac{V_{1}}{V_{2}} = \frac{2\color{Red}{Q_{2}}}{\color{Red}{Q_{2}}} \cdot \frac{T_{1}}{T_{2}} [tex]
[tex] \frac{V_{1}}{V_{2}} = 2 \cdot \frac{T_{1}}{T_{2}} [tex]
Agora, para termos o valor [tex]V_{1}[tex] maior que o valor [tex]V_{1}[tex], devemos teremos [tex] \frac{V_{1}}{V_{2}} > 1 [tex].
[tex] \frac{V_{1}}{V_{2}} = 2 \cdot \frac{T_{1}}{T_{2}} > 1 [tex]
[tex]2 \cdot \frac{T_{1}}{T_{2}} > 1 [tex]
[tex] \frac{T_{1}}{T_{2}} > \frac{1}{2} = 0,5 [tex]
Logo, o estudante 2 fez a afirmação correta.
Portanto, alternativa (B).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Em uma sala escura há um ponto luminoso, a mais de 3 metros de distância de uma parede, e um disco pendurado, paralelo à parede, entre ela e o ponto luminoso. O disco encontra-se a 1 metro de distância do ponto luminoso, projetando uma sombra [tex]S_{1}[tex], em formato de círculo, na parede. Esse disco é afastado mais 2 m do ponto luminoso, em direção à sombra e sem encostar na parede, projetando outra sombra [tex]S_{2}[tex], também no formato de um círculo.
Sejam [tex]A_{1}[tex] a área de [tex]S_{1}[tex] e [tex]A_{2}[tex] a área de [tex]S_{2}[tex].
O valor de [tex]\frac{A_{1}}{A_{2}}[tex] é
Observe as figuras a seguir:


Utilizando semelhança de triângulos nos dois casos temos: ([tex]R_{d}[tex]: raio disco; [tex]R_{s}[tex]: raio da sombra; [tex]r_{d}[tex]: raio disco depois e [tex]R_{S}[tex]: raio da sombra depois).
[tex] \begin{cases} \frac{R_{d}}{R_{s}} = \frac{1}{x} \Longrightarrow R_{s} = R_{d} \cdot x (I) \\ \\ \frac{R_{d}}{r_{s}} = \frac{3}{x} \Longrightarrow R_{d} \cdot x = 3 \cdot r_{s} (II) \end{cases} [tex]
Substituindo a equação (I) em (II), temos:
[tex] R_{s} = 3 \cdot r_{s} [tex]
Como [tex]A_{1}[tex] é a área de [tex]S_{1}[tex] e [tex]A_{2}[tex] a área de [tex]S_{2}[tex]. Então, o valor de [tex]\frac{A_{1}}{A_{2}}[tex] é:
[tex]\frac{A_{1}(antes)}{A_{2}(depois)} = \frac{\color{Red}{π}\ R_{s}^{2}}{\color{Red}{π}\ r_{s}^{2}} = \frac{(3\ \cdot\ r_{s})^{2})}{r_{s}^{2}} = \frac{9\ \color{Red}{r_{s}^{2}}}{\color{Red}{r_{s}^{2}}} = 9 [tex]
Portanto, alternativa (E).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Em 1953, o veterinário francês Monsier LeBeau descobriu que um cão de pequeno porte tem um ritmo de envelhecimento maior do que o de um ser humano, sendo mais acentuado nos dois primeiros anos de vida. Depois desse tempo, esse ritmo de envelhecimento diminui e obtêm-se as seguintes relações:
• um cão de um ano corresponde a um humano de 15 anos;
• um cão de 2 anos corresponde a um humano de 24 anos;
• depois de 2 anos de idade, cada ano vivido por um cão equivale a quatro anos vividos por humanos.
Disponível em: http://online.wsj.com. Acesso em: 16 nov. 2014 (adaptado).
Considere o dia em que um cão de pequeno porte completou 6 anos de idade.
Com base nessas informações, a idade humana, em ano, correspondente à idade desse cão, nesse dia, é
De acordo com as informações do texto, temos:
| Cão | Humano | |
|---|---|---|
| 1 ano | 15 anos | |
| Depois de 2 anos de idade, cada ano vivido por um cão equivale a quatro anos vividos por humanos | 2 anos | 24 anos |
| 3 anos | 28 anos | |
| 4 anos | 32 anos | |
| 5 anos | 36 anos | |
| 6 anos | 40 anos |
Portanto, alternativa (D).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Uma pessoa foi a um supermercado comprar uma caixa de sabão em pó. Lá encontrou várias marcas desse produto, disponibilizado em embalagens com diferentes capacidades e preços. No quadro são fornecidos o preço, em real, e o conteúdo, em quilograma, das embalagens de cinco diferentes marcas de sabão em pó que estão à venda nesse supermercado.
| Marca | Preço por embalagens (R$) | Conteúdo da embalagens (kg) |
|---|---|---|
| I | 18,00 | 3,0 |
| II | 10,00 | 2,5 |
| III | 8,00 | 0,5 |
| IV | 7,00 | 1,0 |
| V | 34,00 | 2,0 |
A marca cuja embalagem oferece o menor preço, em real, por quilograma de sabão em pó é
Cálculo do preço por quilograma de cada marca de sabão em pó:
Marca I:
[tex] \frac{Preço}{kg} = \frac{R \$\ 18,00}{3\ kg} = R \$\ 6,00/kg [tex]
Marca II:
[tex] \frac{Preço}{kg} = \frac{R \$\ 10,00}{2,5\ kg} = \color{Red}{R \$\ 4,00/kg} [tex]
Marca III:
[tex] \frac{Preço}{kg} = \frac{R \$\ 8,00}{0,5\ kg} = R \$\ 16,00/kg [tex]
Marca IV:
[tex] \frac{Preço}{kg} = \frac{R \$\ 7,00}{1\ kg} = R \$\ 7,00/kg [tex]
Marca V:
[tex] \frac{Preço}{kg} = \frac{R \$\ 34,00}{2\ kg} = R \$\ 17,00/kg [tex]
Logo, a marca II oferece o menor preço, em real, por quilograma de sabão em pó.
Portanto, alternativa (B).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Uma piscina de um clube tem o formato de paralelepípedo reto retângulo com 50 m de comprimento, 25 m de largura e 3 m de profundidade. O proprietário do clube construirá duas novas piscinas, de formatos diferentes, e necessita que cada uma tenha o mesmo volume da existente ou o mais próximo possível desse volume. A empresa de construção contratada disponibilizou, para a avaliação desse proprietário, uma proposta com cinco projetos de piscina: três com o formato de cilindro circular reto e duas com o formato de paralelepípedo reto retângulo:
• piscina cilíndrica I ([tex]C_{1}[tex]): 50 m de diâmetro de base e 2 m de profundidade;
• piscina cilíndrica II ([tex]C_{2}[tex]): 40 m de diâmetro de base e 3 m de profundidade;
• piscina cilíndrica III ([tex]C_{3}[tex]): 46 m de diâmetro de base e 2,5 m de profundidade;
• piscina em formato de paralelepípedo I ([tex]P_{1}[tex]): 62 m de comprimento, 24 m de largura e 2 m de profundidade;
• piscina em formato de paralelepípedo II ([tex]P_{1}[tex]): 64 m de comprimento, 30 m de largura e 2 m de profundidade.
Considere 3 como valor aproximado de [tex]π[tex].
Para atender às suas necessidades, dentre os projetos propostos, o proprietário desse clube deverá escolher as piscinas
Cálculo da capacidade da piscina atual:
[tex]V = C \cdot L \cdot h = 50 \cdot 25 \cdot 3 = 3\ 750\ m^{2} [tex]
Agora, encontrar a capacidade de cada piscina:
Piscina [tex](C_{1})[tex]:
[tex]V = π R^{2}h = 3 \cdot 25^{2} \cdot 2 = 6 \cdot 625 = 3\ 750\ m^{2} [tex]
Piscina ([tex]C_{2})[tex]:
[tex]V = π R^{2}h = 3 \cdot 20^{2} \cdot 3 = 9 \cdot 400 = 3\ 600\ m^{2} [tex]
Piscina [tex](C_{3})[tex]:
[tex]V = π R^{2}h = 3 \cdot 23^{2} \cdot 2,5 = 7,5 \cdot 529 = 3\ 967,5\ m^{2} [tex]
Piscina [tex](P_{1})[tex]:
[tex]V = C \cdot L \cdot h = 62 \cdot 24 \cdot 2 = 2\ 976\ m^{2} [tex]
Piscina [tex](P_{2})[tex]:
[tex]V = C \cdot L \cdot h = 64 \cdot 30 \cdot 2 = 3\ 840\ m^{2} [tex]
Logo, a piscina [tex](C_{1})[tex] e [tex](P_{2})[tex] tem o mesmo volume da existente ou o mais próximo possível.
Portanto, alternativa (A).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Um professor de matemática desenvolveu uma atividade educacional relacionada aos Jogos Olímpicos e confeccionou uma maquete que representa uma piscina nas dimensões olímpicas. Admitiu que a piscina olímpica deve ter capacidade mínima de 2 500 000 litros e construiu sua maquete, referente a esse valor mínimo, na forma de paralelepípedo reto retângulo com dimensões internas 2 cm, 25 cm e 50 cm, cujo volume é 2 500 cm³.
Considere que [tex]1 L = 10^{3} cm^{3}[tex].
A maquete confeccionada pelo professor foi elaborada na escala
Como [tex]1 L = 10^{3}\ cm^{3}[tex]. Logo,
Agora, encontrar a escala volumétrica:
[tex]E = \frac{Volume\ da\ maquete}{Volume\ da\ piscina} = \frac{2,5\ L (÷\ 2,5)}{2\ 500\ 000\ L (÷\ 2,5)} = \frac{1}{1\ 000\ 000}[tex]
Por último, fazer a conversão para a escala linear.
[tex] 1 : 1\ 000\ 000[tex]
[tex] \sqrt[3]{1} : \sqrt[3]{1\ 000\ 000}[tex]
[tex] 1 : 100[tex]
Logo, a escala adotada é de [tex]1 : 100[tex].
Portanto, alternativa (A).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Uma imobiliária pôs cinco apartamentos à venda em cinco prédios diferentes de uma cidade brasileira. O quadro apresenta o preço e a área de cada um desses imóveis.
| Apartamento | Área (m²) | Preço (milhares de reais) |
|---|---|---|
| I | 80 | 350 |
| II | 90 | 450 |
| III | 1200 | 480 |
| IV | 130 | 580 |
| V | 135 | 620 |
Um investidor decidiu comprar o apartamento com o menor preço por metro quadrado dentre os cinco apresentados.
Ele deverá comprar o apartamento
Encontrar o preço do m² de cada apartamento:
Apartamento I:
[tex] \frac{Preço}{área} = \frac{R \$\ 350\ 000}{80\ m^{2}} = R \$\ 4\ 375,00/m^{2} [tex]
Apartamento II:
[tex] \frac{Preço}{área} = \frac{R \$\ 450\ 000}{90\ m^{2}} = R \$\ 5\ 000,00/m^{2} [tex]
Apartamento III:
[tex] \frac{Preço}{área} = \frac{R \$\ 480\ 000}{120\ m^{2}} = \color{Red}{R \$\ 4\ 000,00/m^{2}}[tex]
Apartamento IV:
[tex] \frac{Preço}{área} = \frac{R \$\ 580\ 000}{130\ m^{2}} = R \$\ 4\ 461,53/m^{2}[tex]
Apartamento V:
[tex] \frac{Preço}{área} = \frac{R \$\ 620\ 000}{135\ m^{2}} \cong R \$\ 4\ 592,59/m^{2}[tex]
Esse investidor deve comprar o apartamento III.
Portanto, alternativa (C).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Segundo regras da Fifa, em um campo de futebol, a área penal é a região limitada pelo retângulo ABCD, indicado na figura, cujo lado AB mede, aproximadamente, 16 m. O ponto penal P, equidistante dos lados AB e CD, fica localizado a 11 m do lado AD. O arco de circunferência, exterior à região penal, tem centro em P, e o raio mede, aproximadamente, 9 m.

Disponível em: www.cbf.com.br. Acesso em: 5 ago. 2008 (adaptado).
De acordo com as medidas especificadas no texto e na figura, a distância EF entre as extremidades do arco de círculo é
Observe a figura a seguir:

Pelo Teorema de Pitágoras vamos encontrar o valor de [tex]x[tex]:
[tex]a^{2} = b^{2} + c^{2} [tex]
[tex](\overline{EP})^{2} = (\overline{EG})^{2} + (\overline{PG})^{2} [tex]
[tex]9^{2} = x^{2} + 5^{2} [tex]
[tex]81 = x^{2} + 25 [tex]
[tex]81 - 25 = x^{2} [tex]
[tex]56 = x^{2} [tex]
[tex]x = \sqrt{56} [tex]
[tex]x \cong 7,48\ m [tex]
Logo, o comprimento EF é:
[tex] (\overline{EP}) = 2x [tex]
[tex] (\overline{EP}) \cong 2 \cdot 7,48 [tex]
[tex] (\overline{EP}) \cong 14,97 [tex]
Ou seja é superior a 14 m e inferior a 19 m.
Portanto, alternativa (C).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Veja o gasto médio de calorias, por hora de atividade, quando são exercidas algumas atividades domésticas:
• varrer o chão: 200 calorias;
• passar aspirador de pó: 350 calorias;
• limpar janelas: 260 calorias.
Disponível em: www.corpoacorpo.uol.com.br. Acesso em: 4 dez. 2017 (adaptado).
Uma pessoa varreu o chão da casa, depois passou o aspirador de pó e, por fim, limpou as janelas, gastando 30 minutos em cada atividade, sem parar para descansar. Considere que o gasto de calorias em uma atividade varie proporcionalmente em relação ao tempo.
O gráfico que melhor representa o gasto acumulado de calorias dessa pessoa durante as atividades desenvolvidas é
Como o gasto de calorias entre as atividades variam proporcionalmente em relação ao tempo. Logo, temos:
• varrer o chão: 200 ou 100 calorias;
• passar aspirador de pó: 350 ou 175 calorias;
• limpar janelas: 260 ou 130 calorias.
Dessa forma, o gráfico A satisfaz a condição pedida. Ou seja:
[tex]0 + 100 = 100\ cal [tex]
[tex]100 + 175 = 275\ cal[tex]
[tex] 275 + 130 = 405\ cal [tex]

Portanto, alternativa (A).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Uma quadra oficial de futebol de salão ocupa uma área que corresponde à área de um retângulo com comprimento de 40 m e largura de 20 m. Para segurança dos atletas, as linhas demarcatórias da quadra, nas laterais e nos fundos, deverão estar a uma distância de, no mínimo, 2 m de obstáculos que não fazem parte da quadra, tais como rede de proteção, tela, grade ou parede.
Disponível em: www.cbfs.com.br. Acesso em: 20 out. 2019 (adaptado).
A gerência do Departamento de Obras de uma Prefeitura avalia adquirir um terreno e nele construir uma quadra oficial de futebol de salão. Há cinco terrenos disponíveis, e a gerência comprará o terreno que tiver menor área, desde que comporte a construção da quadra garantindo todas as demandas que ofereçam segurança aos atletas. Planeja-se ainda que a quadra seja construída de modo que o seu lado maior seja paralelo à rua. A figura ilustra os terrenos disponíveis e que estão sendo avaliados.

Qual dos cinco terrenos a gerência deve adquirir a fim de atender a todas as exigências apresentadas?
Como a quadra corresponde à área de um retângulo com comprimento de 40 m e largura de 20 m, e tem uma distância de, no mínimo, 2 m de obstáculos que não fazem parte da quadra. Sendo assim, as dimensões da quadra é:

Agora, fazer a análise dos tipos de terrenos e encontrar o ideal:
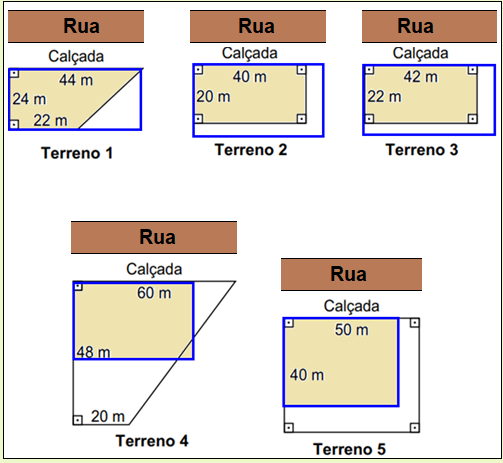
Dessa forma, o único terreno que satisfaz as condições pedidas é o 5.
Portanto, alternativa (E).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Uma empresa produziu uma bola de chocolate, em formato esférico, para utilizar na decoração de sua loja. Essa bola tem 20 cm de diâmetro externo, sendo oca por dentro, e a medida da espessura entre as superfícies interna e externa corresponde a 1 cm. Considere que, na confecção dessa bola, foi utilizado um tipo de chocolate em que 1 g equivale a 0,75 cm³.
A quantidade de chocolate, em grama, utilizado na confecção dessa bola é
Observe o esquema a seguir:

Agora, encontrar o volume de chocolate:
[tex] V_{(chocolate)} = V_{(esfera\ maior)} - V_{(esfera\ menor)} [tex]
[tex] V_{(chocolate)} = \frac{4πR^{3}}{3} - \frac{4πr^{3}}{3} [tex]
[tex] V_{(chocolate)} = \frac{4\ \cdot\ π\ \cdot\ 10^{3}}{3} - \frac{4\ \cdot\ π\ \cdot\ 9^{3}}{3} [tex]
[tex] V_{(chocolate)} = \frac{4\ \cdot\ π\ \cdot\ 1000}{3} - \frac{4\ \cdot\ π\ \cdot\ 729}{3} [tex]
[tex] V_{(chocolate)} = \frac{4\ 000π}{3} - \frac{2\ 916 π }{3} [tex]
[tex] V_{(chocolate)} = \frac{1\ 084π}{3}\ cm^{3} [tex]
Agora, encontrar a massa de chocolate sabendo que 1 g equivale a 0,75 cm³:
[tex]1\ g\ -----\ 0,75 = \frac{75}{100} = \frac{3}{4}\ cm^{3} [tex]
[tex]x\ g\ -----\ \frac{1\ 084π}{3}\ cm^{3}[tex]
[tex] \frac{3}{4} x\ =\ \frac{1\ 084π}{3}[tex]
[tex] x\ =\ \frac{1\ 084π \cdot 4}{3 \cdot 3}[tex]
[tex] x\ =\ \frac{4\ 336π}{9}[tex]
Portanto, alternativa (C).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Duas empresas do mercado de pequenos reparos domésticos determinam o valor de seus serviços a partir de um valor fixo acrescido de um valor cobrado por hora. A empresa X cobra R$ 60,00 de valor fixo mais R$ 18,00 por hora de serviço prestado. A empresa Y cobra R$ 24,00 de valor fixo e está definindo um novo valor a ser cobrado por hora. Sua estratégia de mercado prevê que, em relação à empresa X, o custo total do serviço deve ser menor ou igual para trabalhos de até duas horas de duração.
Qual é o valor máximo, em real, que a empresa Y poderá cobrar por hora de serviço prestado a fim de atender à sua estratégia de mercado?
Equacionando o problema:
Empresa X: [tex] V = fixo\ +\ variável = 60 + 18t [tex]
Empresa Y: [tex] V = fixo\ +\ variável = 24 + mt [tex]
Como a relação à empresa X, o custo total do serviço deve ser menor ou igual para trabalhos de até duas horas (2 horas) de duração. Logo:
[tex] V_{Y} ≤ V_{X} [tex]
[tex] 24 + mt ≤ 60 + 18t [tex]
[tex] 24 + m \cdot 2 ≤ 60 + 18 \cdot 2 [tex]
[tex] 24 + 2m ≤ 60 + 36 [tex]
[tex] 2m ≤ 60 + 36 - 24 [tex]
[tex] 2m ≤ 72 [tex]
[tex] m ≤ \frac{72}{2} [tex]
[tex] m ≤ 36 [tex]
Portanto, alternativa (B).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
O síndico de um condomínio contratou uma empresa para verificar a qualidade da água dos cinco reservatórios que alimentam esses edifícios. A empresa utiliza um teste que fornece o valor de um parâmetro, expresso em pontos que variam de 0 a 100, que indicam a qualidade da água, sendo o valor 0 associado à péssima qualidade e 100 associado à ótima qualidade da água. Quando esse parâmetro assume um valor a partir de 50 pontos, a água é considerada de qualidade adequada.
Para os reservatórios I, II, III e IV, esse parâmetro assumiu, respectivamente, os valores 64, 53, 63 e 64 nesse tipo de teste. Já no reservatório V, esse parâmetro foi de 20 pontos, reprovando a qualidade da água. Com isso, a água desse reservatório será tratada de modo a aumentar sua qualidade.
O síndico pretende que o parâmetro de qualidade da água do reservatório V aumente o suficiente para que a média dos parâmetros de qualidade da água dos cinco reservatórios seja, no mínimo, igual a 60 pontos.
A quantidade mínima de pontos que o parâmetro da qualidade da água do reservatório V deve aumentar é
Dados:
Reservatório I: 64
Reservatório II: 53
Reservatório III: 63
Reservatório IV: 64
Reservatório V: 20
Então, o reservatório V deve ser tratado de modo a aumentar sua qualidade. Vamos chamar de x o aumento de parâmetro. Logo:
[tex] Média = \frac{R_{(I)}\ +\ R_{(II)}\ +\ R_{(III)}\ +\ R_{(IV)}\ +\ R_{(V)}}{5} [tex]
[tex] 60 = \frac{64\ +\ 53\ +\ 63\ +\ 64\ +\ (x\ +\ 5) }{5} [tex]
[tex] 300 = 64\ +\ 53\ +\ 63\ + 64\ +\ x\ +\ 5 [tex]
[tex] 300 = 264 + x [tex]
[tex] 300 - 264 = x [tex]
[tex] x = 36 [tex]
Portanto, alternativa (A).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Após uma reforma, um clube decide comprar duchas para serem instaladas no vestiário. O tipo de ducha escolhida, segundo o fabricante, tem probabilidade igual a [tex]\frac{1}{10}[tex] de apresentar funcionamento irregular. O administrador do clube planeja adquirir uma certa quantidade dessas duchas, de forma que a probabilidade de que pelo menos uma das duchas adquiridas apresente funcionamento regular seja igual a, no mínimo, [tex]\frac{99}{100}[tex].
A quantidade mínima de duchas que deverá ser adquirida para atender ao planejamento desse administrador é
Para adquirir uma certa quantidade dessas duchas, de forma que a probabilidade de que pelo menos uma das duchas adquiridas apresente funcionamento REGULAR seja igual a, no mínimo, [tex]\frac{99}{100}[tex]. Então, para ser IRREGULAR deve ser de [tex]\frac{1}{10}[tex]. Então:
[tex]P = 1ª\ torneira\ \cdot\ 2ª\ torneira\ \cdot\ ... [tex]
[tex]P = \frac{1}{10} \cdot \frac{1}{10} [tex]
[tex]P = \frac{1}{100} [tex]
Sendo assim, 2 torneiras é a quantidade mínima de duchas que deverá ser adquirida para atender ao planejamento desse administrador.
Portanto, alternativa (A).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Na modelagem e no estudo de fenômenos periódicos, em geral, os modelos associados fazem uso de funções trigonométricas. Nesse sentido, considere um experimento, realizado em laboratório, em que uma planta foi colocada em uma estufa, onde a temperatura é controlável. O experimento consiste em observar alterações nas características dessa planta ao ser submetida a variações de temperatura. Durante 24 horas, a temperatura [tex]T(x)[tex] da estufa variou de acordo com a função [tex]T(x) = 20\ -\ 10\ sen(π\ \cdot\ \frac{x}{4})[tex], em que [tex]x[tex] é medido em hora, variando no intervalo [tex]0 ≤ x ≤ 24[tex].
Durante esse experimento, quantas vezes a temperatura na estufa atingiu o seu valor mínimo?
Analisando a função [tex]T(x) = 20\ -\ 10\ sen(π\ \cdot\ \frac{x}{4})[tex] teremos valor mínimo em [tex]\frac{π}{2} [tex], ou seja, 90°.
Dessa forma, encontrar a quantidade de vezes terá valor mínimo.
1ª volta: [tex]\frac{π}{2} [tex]
[tex]\frac{x\ \cdot\ π}{4} = \frac{π}{2} \Longrightarrow x = \frac{4\ \cdot\ \color{Red}{π}}{2\ \cdot\ \color{Red}{π}} = 2\ horas[tex] (1ª vez)
2ª volta: [tex]\frac{π}{2} + 2π = \frac{5π}{2} [tex]
[tex]\frac{x\ \cdot\ π}{4} = \frac{5π}{2} \Longrightarrow x = \frac{4\ \cdot\ \color{Red}{5π}}{2\ \cdot\ \color{Red}{π}} = 10\ horas[tex] (2ª vez)
3ª volta: [tex]\frac{5π}{2} + 2π = \frac{9π}{2} [tex]
[tex]\frac{x\ \cdot\ π}{4} = \frac{9π}{2} \Longrightarrow x = \frac{4\ \cdot\ \color{Red}{9π}}{2\ \cdot\ \color{Red}{π}} = 18\ horas[tex] (3ª vez)
4ª volta: [tex]\frac{9π}{2} + 2π = \frac{13π}{2} [tex]
[tex]\frac{x\ \cdot\ π}{4} = \frac{13π}{2} \Longrightarrow x = \frac{4\ \cdot\ \color{Red}{13π}}{2\ \cdot\ \color{Red}{π}} = 26\ horas[tex] (Não satisfaz!)
Portanto, alternativa (B).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
A nota final de um estudante em uma disciplina é dada pela mediana das notas de suas quatro provas. Cinco estudantes dessa disciplina obtiveram as notas apresentadas no quadro.
| Estudante | Prova 1 | Prova 2 | Prova 3 | Prova 4 |
|---|---|---|---|---|
| I | 85 | 45 | 90 | 45 |
| II | 80 | 70 | 70 | 75 |
| III | 75 | 75 | 75 | 55 |
| IV | 85 | 35 | 35 | 90 |
| V | 60 | 70 | 70 | 7 |
O professor dessa disciplina pediu a cada estudante que calculasse sua nota final e lhe apresentasse o resultado obtido. Os resultados informados pelos estudantes foram:
• estudante I: 77;
• estudante II: 70;
• estudante III: 70;
• estudante IV: 60;
• estudante V: 70.
Qual(is) estudante(s) acertou(aram) sua nota final?
Primeiro ordenar as notas para encontrar a mediana de cada estudante:
Estudante I:
[tex] 45 - \color{Red}{45 - 85} - 90 \Longrightarrow mediana = \frac{45\ +\ 85}{2} = \frac{130}{2} = 65 [tex]
Estudante II:
[tex] 70 - \color{Red}{70 - 75} - 80 \Longrightarrow mediana = \frac{70\ +\ 75}{2} = \frac{145}{2} = 72,5 [tex]
Estudante III:
[tex] 55 - \color{Red}{75 - 75} - 55 \Longrightarrow mediana = \frac{75\ +\ 75}{2} = \frac{150}{2} = 75 [tex]
Estudante IV:
[tex] 35 - \color{Red}{35 - 85} - 90 \Longrightarrow mediana = \frac{35\ +\ 85}{2} = \frac{120}{2} = 60 [tex]
Estudante V:
[tex] 60 - \color{Red}{70 - 70} - 75 \Longrightarrow mediana = \frac{70\ +\ 70}{2} = \frac{140}{2} = 70 [tex]
Portanto, os estudantes IV e V acertaram sua nota final.
Portanto, alternativa (E).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
A tartaruga ou tachão de trânsito é um dispositivo de sinalização horizontal utilizado para canalizar o tráfego ou garantir o afastamento do fluxo de veículos de zonas perigosas ou com grande risco de acidentes. A Figura 1 apresenta alguns deles já instalados.

Figura 1
Disponível em: www.alfasinalizacao.com.br. Acesso em: 28 nov. 2021 (adaptado).
O modelo geométrico de um tachão está representado na Figura 2. Ele é formado por duas faces retangulares paralelas e quatro faces trapezoidais. Suas arestas laterais, se prolongadas, concorrem em um mesmo ponto.

Figura 2
Qual é o sólido representado pelo modelo geométrico do tachão?
O modelo geométrico do tachão é um tronco de pirâmide quadrangular.
Portanto, alternativa (E).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Os candidatos A, B e C participaram de um concurso composto por uma prova de Matemática, uma de Português e outra de Geografia, sendo os pesos dessas três provas diferentes. As notas obtidas por esses três candidatos e os pesos atribuídos a essas provas estão representados nas tabelas:
Tabela I (Notas)
| Candidato | Matemática | Português | Geografia |
|---|---|---|---|
| A | 9 | 6 | 7 |
| B | 8 | 7 | 8 |
| C | 9 | 5 | 6 |
Tabela II (Pesos)
| Matérias | Pesos |
|---|---|
| Matemática | 3 |
| Português | 2 |
| Geografia | 1 |
As notas finais são obtidas somando-se os produtos das notas pelos respectivos pesos. As notas finais dos três candidatos podem ser obtidas multiplicando-se a matriz das notas dos três candidatos nas três provas pela matriz dos pesos das três provas.
A matriz das notas finais dos três candidatos é
Efetuando a multiplicação das matrizes:
[tex]= \begin{pmatrix} 9 & 6 & 7 \\ 8 & 7 & 8 \\ 9 & 5 & 6 \end{pmatrix} \cdot \begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix}[tex]
[tex]= \begin{pmatrix} 9 \cdot 3 + 6 \cdot 2 + 7 \cdot 1 \\ 8 \cdot 3 + 7 \cdot 2 + 8 \cdot 1 \\ 9 \cdot 3 + 5 \cdot 2 + 6 \cdot 1 \end{pmatrix} [tex]
[tex]= \begin{pmatrix} 27 + 12 + 7 \\ 24 + 14 + 8 \\ 27 + 10 + 6 \end{pmatrix} [tex]
[tex]= \begin{pmatrix}46 \\ 46 \\ 43 \end{pmatrix} [tex]
Dessa forma, a matriz das notas finais dos três candidatos é [tex]\begin{pmatrix}46 \\ 46 \\ 43 \end{pmatrix}[tex].
.Portanto, alternativa (B).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Um funcionário de uma loja de computadores misturou, por descuido, três computadores defeituosos com sete computadores perfeitos que estavam no estoque. Uma pequena empresa fez a compra de cinco computadores nessa loja, escolhendo-os aleatoriamente dentre os dez que estavam no estoque.
Qual é a probabilidade de essa empresa ter levado, em sua compra, todos os três computadores defeituosos?
Primeiro encontrar a quantidade total de combinações dos 10 computadores tomados de 5 em 5.
[tex] C_{10,\ 5} = \frac{10!}{5!\ (10\ -\ 5)!)} = \frac{10\ \cdot\ 9\ \cdot\ 8\ \cdot\ 7\ \cdot\ 6\ \cdot\ \color{Red}{5!}}{5!\ \color{Red}{5!}} = \frac{10\ \cdot\ 9\ \cdot\ 8\ \cdot\ 7\ \cdot\ 6}{5!} [tex]
[tex] C_{10,\ 5} = \frac{\color{blue}{10}\ \cdot\ 9\ \cdot\ \color{green}{8}\ \cdot\ 7\ \cdot\ \color{Red}{6}}{\color{blue}{5}\ \cdot\ \color{green}{4}\ \cdot\ \color{Red}{3\ \cdot\ 2}\ \cdot\ 1} = 2 \cdot 9 \cdot 2 \cdot 7 [tex]
Agora, encontrar a quantidade de combinações dos 7 computadores tomados de 2 em 2.
[tex] C_{7, 2} = \frac{7!}{2!\ (7\ -\ 2)!} = \frac{7\ \cdot\ \color{blue}{6}\ \cdot\ \color{Red}{5!}}{\color{blue}{2!}\ \color{Red}{\cdot\ 5!}} = 7 \cdot 3 [tex]
Agora, encontrar a probabilidade:
[tex]P = \frac{C_{7,\ 2}}{C_{10,\ 5}} = \frac{{\color{blue}{7}\ \cdot\ \color{Red}{3}}}{2\ \cdot\ \color{Red}{9}\ \cdot\ 2\ \cdot\ \color{blue}{7}} = \frac{1}{2\ \cdot\ 3\ \cdot\ 2} = \frac{1}{12} [tex]
Portanto, alternativa (B).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Uma empresa fundada em 2005, ao longo dos anos ganhou popularidade e aumentou consideravelmente sua atuação na economia do país. Os lucros anuais e seu padrão de crescimento podem ser observados na tabela.
| Ano | Lucro (em milhares de reais) |
|---|---|
| 2005 | 3 |
| 2006 | 5 |
| 2007 | 9 |
| 2008 | 17 |
| 2009 | 33 |
| ... | ... |
Supondo que se tenha mantido o padrão observado na tabela para os 5 anos seguintes, estima-se que o lucro total dessa empresa, de 2005 a 2014, em milhar de real, foi
Mantendo o padrão podemos construir uma tabela:
| Ano | Lucro (em milhares de reais) |
|---|---|
| 2005 | 3 |
| 2006 | 5 = 3 + 2 |
| 2007 | 9 = 5 + 4 |
| 2008 | 17 = 9 + 8 |
| 2009 | 33 = 17 + 16 |
| 2010 | 65 = 33 + 32 |
| 2011 | 129 = 65 + 64 |
| 2012 | 257 = 129 + 128 |
| 2013 | 513 = 257 + 256 |
| 2014 | 1 025 = 513 + 512 |
Agora, encontrar o lucro total:
[tex] L = 3 + 5 + 9 + 17 + 33 + 65 + 129 + 257 + 513 + 1\ 025 [tex]
[tex] L = 2\ 056\ mil\ reais [tex]
Portanto, alternativa (D).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
“Quanto é mil trilhões Vezes infinito?”
TOLLER, P. Oito anos. In: Paula Toller. Rio de Janeiro: Warner Music Brasil, 1998.
O trecho da canção Oito anos, de Paula Toller, foi apresentado por um professor de matemática a um grupo de cinco alunos. Em seguida, o professor solicitou que cada aluno apresentasse uma expressão matemática que traduzisse os versos citados. Cinco respostas diferentes foram dadas:
Resposta 1: [tex] 10^{9} × ∞ [tex]
Resposta 2: [tex]10^{12} × ϕ [tex]
Resposta 3: [tex]10^{12} × ∞ [tex]
Resposta 4: [tex]10^{15} × ϕ [tex]
Resposta 5: [tex]10^{15} × ∞ [tex]
A resposta que representa matematicamente o trecho da canção é a
A resposta que representa matematicamente o trecho da canção é:
[tex]= mil\ trilhões\ vezes\ infinito [tex]
[tex]= 1\ 000\ ×\ 1\ 000\ 000\ 000\ 000\ ×\ ∞ [tex]
[tex]= 10^{3}\ ×\ 10^{12}\ ×\ ∞ [tex]
[tex]= 10^{15}\ ×\ ∞ [tex]
Portanto, o aluno da resposta 5 acertou.
Portanto, alternativa (E).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Uma câmara de resfriamento de um laboratório tem um dispositivo que, ao ser ajustado, alterará a temperatura, em grau Celsius, de um líquido ao final de cada minuto. Nessa câmara, existem dois visores, o primeiro indicando o quanto a temperatura do líquido deve ser diminuída ao final de cada minuto, e o segundo indicando a temperatura do líquido na câmara naquele instante.
Foi iniciado um teste nessa câmara quando um líquido, à temperatura de 30 °C, foi colocado em seu interior. Ela estava programada no primeiro visor em 1,4 °C. No final de 5 minutos, foi alterada a temperatura, e o valor da mudança que aparecia no primeiro visor foi diminuído em 0,5 °C. Ao final de 15 minutos do início do teste, a temperatura registrada no primeiro visor foi aumentada em 0,3 °C em relação à última marcação.
Um dos objetivos desse teste é que, ao final de 30 minutos, a temperatura do líquido seja de 0 °C. Assim, após 25 minutos relativamente ao início do teste, novo ajuste deve ser feito na numeração do primeiro visor.
Que alteração deverá ser feita na numeração do primeiro visor ao final de 25 minutos do início do teste?
1ª etapa: (0 a 5 minutos)
Ao iniciar o teste a temperatura era de 30° e no primeiro visor estava marcando 1,4°C.
[tex]= 1,4°C \cdot 5\ min = 7°C [tex]
Com isso, a temperatura ficou:
[tex]= 30°C\ -\ 7°C = 23°C [tex]
2ª etapa: (5 a 15 minutos): (0 a 5 minutos)
Ao final dos primeiros 5 minutos, o valor da mudança que aparecia no primeiro visor foi diminuído em 0,5 °C. Logo:
[tex]= 1,4°C\ -\ 0,5° = 0,9°C [tex]
Logo,
[tex]= 0,9°C \cdot 10\ min = 9°C [tex]
Dessa forma,
[tex]= 23°C\ -\ 9°C = 14°C [tex]
3ª etapa: (15 a 25 minutos)
Ao final de 15 minutos do início do teste, a temperatura registrada no primeiro visor foi aumentada em 0,3 °C em relação à última marcação. Logo,
[tex]= 0,9°C\ +\ 0,3° = 1,2°C [tex]
Logo,
[tex]= 1,2°C \cdot 10\ min = 12°C [tex]
Dessa forma,
[tex]= 14°C\ -\ 12°C = 2°C [tex]
4ª etapa (final):: (25 a 30 minutos)
Como o objetivo desse teste é que, ao final de 30 minutos, a temperatura do líquido seja de 0 °C. Como está em 2°C e deve chegar a 0°C. Dessa forma:
[tex]x \cdot 5\ min = 2°C [tex]
[tex]x = \frac{2°C}{5\ min} = 0,4\ °C/min [tex]
Como a temperatura estava em 1,2°C para chegar em 0,4°C deve-se:
[tex]= 1,2°C\ -\ 0,8°C = 0,4°C [tex]
Portanto, deve-se diminuir em 0,8°C.
Portanto, alternativa (D).
(Créditos da resolução: Prof. Warles)
(ENEM 2023 - 2ª Aplicação - PPL).
Em radiometria, a potência radiante emitida por uma fonte de radiação é diretamente proporcional à quantidade de energia, em joule (J), irradiada pela fonte, e inversamente proporcional ao intervalo de tempo, em segundo (s), que a fonte necessita para emitir essa energia. Por meio de sensores adequados, localizados em diferentes distâncias da fonte, medidas em metro (m), é possível medir a potência radiante por unidade de área que chega àquela posição.
A expressão que representa a unidade de medida para a grandeza potência radiante por unidade de área é
A potência radiante por unidade de área é:
[tex]\frac{Potência}{Área} = \frac{\frac{Energia}{tempo}}{área} = \frac{\frac{Joule}{segundos}}{m^{2}} = \frac{\frac{J}{s}}{m^{2}} = \frac{J}{s} \cdot \frac{1}{m^{2}} = \frac{J}{s\ \cdot\ m^{2}} [tex]
Portanto, alternativa "E".
(Créditos da resolução: Prof. Warles)
