(ENEM 2017 - 2ª Aplicação).
Em certa loja de roupas, o lucro na venda de uma camiseta e de 25% do preço de custo da camiseta pago pela loja. Já o lucro na venda de uma bermuda é de 30% do preço de custo da bermuda, e na venda de uma calça o lucro é de 20% sobre o preço de custo da calça. Um cliente comprou nessa loja duas camisetas, cujo preço de custo foi R$ 40,00 cada uma, uma bermuda que teve preço de custo de R$ 60,00 e duas calças, ambas com mesmo preço de custo. Sabe-se que, com essa compra, o cliente proporcionou um lucro de R$ 78,00 para a loja.
Considerando essas informações, qual foi o preço de custo, em real, pago por uma calça?
Lucro de venda da camiseta: 25% = 0,25
Lucro de venda da bermuda: 30% = 0,3
Lucro de venda da calça: 20% = 0,2
2 camisetas + 1 bermuda + 2 calças = 78
2 ∙ 40 ∙ 0,25 + 60 ∙ 0,3 + 2 ∙ x ∙ 0,2 = 78
20 + 18 + 0,4x = 78
0,4x = 78 – 20 – 18
0,4 x = 40
x = 100
(ENEM 2017 - 2ª Aplicação).
Um marceneiro recebeu a encomenda de um a passarela de 14.935 m sobre um pequeno lago, conforme a Figura I. A obra será executada com tábuas de 10 cm de largura, que já estão com o comprimento necessário para instalação, deixando-se um espaçamento de 15 mm entre tábuas consecutivas. de acordo com a planta do projeto na Figura II.

Desconsiderando-se eventuais perdas com cortes durante a execução do projeto, quantas tábuas, no mínimo, o marceneiro necessitará para a execução da encomenda?
Tábua = x
espaçamento = 15 mm = 15 : 10 = 1,5 cm
largura da tábua = 10 cm
passarela = 14,935 m = 1493,5 cm
[tex] x \cdot\ (10\ +\ 1,5) = 1493,5 [tex]
[tex] x = \frac{1493,5}{10 + 1,5} =\frac{1493,5}{11,5} = 129,86\ tábuas [tex]
Logo, são necessários aproximadamente 130 tábuas.
(ENEM 2017 - 2ª Aplicação).
Estimativas do IBGE para a safra nacional de cereais, leguminosas e oleaginosas, em 2012, apontavam um a participação por região conforme indicado no gráfico.

As estimativas indicavam que as duas regiões maiores produtoras produziriam, juntas, um total de 119,9 milhões de toneladas dessas culturas, em 2012.
Disponível em: www.ibge.gov.br. Acesso em: 3 jul. 2012.
De acordo com esses dados, qual seria o valor mais próximo da produção, em milhão de tonelada, de cereais, leguminosas e oleaginosas, em 2012, na Região Sudeste do pais?
Sul + Centro-Oeste = 37,2% + 38,3% = 75,5 %
75,5 % --------- 119,9 milhões de toneladas
11,4 % ---------- x
[tex] x = \frac{11,4\ \cdot 119,9}{75,5} = \frac{1366,86}{75,5} = 18,10 [tex]%
(ENEM 2017 - 2ª Aplicação).
No próximo fim de semana, uma pessoa receberá visitas em sua casa, precisando, portanto, comprar refrigerante. Para isso, ela fez a pesquisa de preços em dois supermercados e montou esta tabela.

Ela pretende comprar apenas garrafas que tenham a mesma capacidade.
Independentemente de em qual supermercado essa pessoa fará a compra, a fim de ter o menor custo, ela deverá adquirir garrafas com que capacidade?
Para verificar vamos converter para 1 litro:
• Para 0,5 L: Super. (A): R$ 2,10 ∙ 2 = R$ 4,20 e Super. (B): R$ 2,00 ∙ 2 = R$ 4,00
• Para 1,5 L: Super. (A): R$ 2,70 ∙ 2/3 = R$ 1,80 e Super. (B): R$ 3,00 ∙ 2/3 = R$ 2,00
• Para 2,0 L: Super. (A): R$ 4,20 : 2 = R$ 2,10 e Super. (B): R$ 3,20 : 2 = R$ 1,60
• Para 2,5 L: Super. (A): R$ 6,00 ∙ 2/5 = R$ 2,40 e Super. (B): R$ 4,70 ∙ 2/5 = R$ 1,88
• Para 3,0 L: Super. (A): R$ 6,90 : 3 = R$ 2,30 e Super. (B): R$ 5,00 : 3 = R$ 1,66
Logo, o menor custo é comprar garrafas de 2L no supermercado B.
(ENEM 2017 - 2ª Aplicação).
Em uma embalagem de farinha encontra-se a receita de um bolo, sendo parte dela reproduzida a seguir:

Possuindo apenas a colher medida indicada na receita, uma dona de casa teve que fazer algumas conversões para poder medir com precisão a farinha. Considere que a farinha e o fermento possuem densidades iguais.
Cada xícara indicada na receita é equivalente a quantas colheres medidas?
Descobrindo a quantidade gramas tem uma xícara:
640g ------- 4 xícaras
x g -------1 xícara
[tex] x = \frac{640}{4} = 160\ g [tex]
Agora, encontrar a quantidade gramas tem uma colher.
16 g ------- 2 colheres
x g ------- 1 colher
[tex] x = \frac{16}{2} = 8\ g [tex]
Por último, temos:
[tex] N°\ de\ colheres = \frac{1\ xícara\ (g)}{1\ colher\ (g)} = \frac{160}{8} = 20 [tex]
(ENEM 2017 - 2ª Aplicação).
Numa tarefa escolar, um aluno precisava fazer a planta baixa de sua casa em uma escala de 1 : 40. Ele verificou que a base da casa era retangular, tendo 12 metros de comprimento e 8 metros de largura. O aluno foi a uma papelaria e lá observou que havia cinco tipos de folhas de papel, todas com diferentes dimensões. O quadro contém os cinco tipos de folhas, com seus comprimentos e larguras fornecidos em centímetro.

O aluno analisou os cinco tipos de folha e comprou a que possuía as dimensões mínimas necessárias para que ele fizesse a planta de sua casa na escala desejada, deixando exatamente 2 centímetros de margem em cada um dos quatro lados da folha.
A folha escolhida pelo aluno foi a de tipo
A base da casa é retangular com 12 m de comprimento e 8 m de largura.
Agora, analisando a escala 1 : 40.
Comprimento:
1 cm ----------- 40 cm
x cm ------------ 1200 cm = (12 m)
[tex] x = \frac{1200}{40} = 30\ cm [tex]
Largura:
1 cm ----------- 40 cm
x cm ------------ 800 cm = (8 m)
[tex] x = \frac{800}{40} = 20\ cm [tex]
Agora, analisando as condições da planta baixa, deixando 2 cm na margem da folha. Assim, temos:
comprimento: 30 cm + 2 cm + 2 cm = 34 cm
largura: 20 cm + 2 cm + 2 cm = 24 cm
Portanto, a folha que satisfaz é a IV.
(ENEM 2017 - 2ª Aplicação).
Uma escola organizou uma corrida de revezamento 4 x 400 metros, que consiste em uma prova esportiva na qual os atletas correm 400 metros cada um deles, segurando um bastão, repassando-o de um atleta para outro da mesma equipe, realizando três trocas ao longo do percurso, até o quarto atleta, que cruzará a linha de chegada com o bastão. A equipe ganhadora realizou a prova em um tempo total de 325 segundos.
O segundo corredor da equipe ganhadora correu seus 400 metros 15 segundos mais rápido do que o primeiro; já o terceiro realizou seus 400 metros 5 segundos mais rápido que o segundo corredor, e o último realizou seu percurso em 3/4 do tempo realizado pelo primeiro.
Qual foi o tempo, em segundo, em que o último atleta da equipe ganhadora realizou seu percurso de 400 metros?
1° atleta: x
2° atleta: x - 15
3° atleta: (x - 15) - 5 = x - 20
4° atleta: [tex] \frac{3x }{4} [tex]
1° atleta + 2° atleta + 3° atleta + 4° atleta = 325
[tex] x + x - 15 + x - 20 + \frac{3x }{4} = 325 [tex]
[tex] \frac{ 4x\ +\ 4x\ -\ 60\ +\ 4x\ -\ 80\ +\ 3x\ = 1300 }{4} [tex]
[tex] 4x + 4x - 60 + 4x - 80 + 3x = 1300[tex]
[tex] 15x = 1440 [tex]
[tex] x = \frac{1440 }{15} = 96\ segundos [tex]
Logo, o último atleta fez:
[tex] \frac{3x}{4} = \frac{3\ \cdot\ 96}{4} = \frac{288}{4} = 72\ segundos [tex]
(ENEM 2017 - 2ª Aplicação).
Uma fábrica de papel higiênico produz embalagens com quatro rolos de 30 m cada, cujo preço para o consumidor é R$ 3,60. Uma nova embalagem com dez rolos de 50 m cada, de mesma largura, será lançada no mercado. O preço do produto na nova embalagem deve ser equivalente ao já produzido, mas, para incentivar as vendas, inicialmente o preço de venda terá um desconto de 10%.
Para que isso aconteça, o preço de venda da nova embalagem, em real, deve ser
Embalagens (4 rolos - 30 m) → R$ 3,60
embalagens nova (10 rolos - 50 m) → R$ ???
4 x 30 m = 120 m ------------ R$ 3,60
10 x 50 m = 500 m ----------- x
[tex] x = \frac{500\ \cdot\ 3,60}{120} = \frac{1800}{120} = R$ 15,00 [tex]
Agora, tendo o desconto de 10% no preço de venda.
15,00 x 0,9 = R$ 13,50.
(ENEM 2017 - 2ª Aplicação).
O hábito cristalino é um termo utilizado por mineralogistas para descrever a aparência típica de um cristal em termos de tamanho e forma. A granada é um mineral cujo hábito cristalino é um poliedro com 30 arestas e 20 vértices. Um mineralogista construiu um modelo ilustrativo de um cristal de granada pela junção dos polígonos correspondentes às faces.
Supondo que o poliedro ilustrativo de um cristal de granada é convexo, então a quantidade de faces utilizadas na montagem do modelo ilustrativo desse cristal é igual a
Dados: A = 30 arestas, V = 20 vértices e F = ?
F + V = A + 2
F + 20 = 30 + 2
F = 32 – 20
F = 12 faces
(ENEM 2017 - 2ª Aplicação).
Um sistema de depreciação linear, estabelecendo que após 10 anos o valor monetário de um bem será zero, é usado nas declarações de imposto de renda de alguns países. O gráfico ilustra essa situação.

Uma pessoa adquiriu dois bens, A e B, pagando 1 200 e 900 dólares, respectivamente.
Considerando as informações dadas, após 8 anos, qual será a diferença entre os valores monetários, em dólar, desses bens?
Para 1200 dólares: (10, 0) e (0, 1200)
calculo do coeficiente angular:
[tex] m = \frac{y_{2} - y_{1}}{ x_{2} - x_{1}} = \frac{1200 - 0}{0 - 10} = \frac{1200}{- 10} = - 120 [tex]
Logo, (8, y)
y = – 120 ∙ 8 + 1200
y = – 960 + 1200
y = $ 240
Para 900 dólares: (10, 0) e (0, 900)
calculo do coeficiente angular:
[tex] m = \frac{y_{2} - y_{1}}{ x_{2} - x_{1}} = \frac{900 - 0}{0 - 10} = \frac{900}{- 10} = - 90 [tex]
Logo, (8, y)
y = – 90 ∙ 8 + 900
y = – 720 + 900
y = $ 180
Portanto, a diferença é:
$ 240 – $ 180 = $ 60,00
(ENEM 2017 - 2ª Aplicação).
Um programa de televisão criou um perfil em uma rede social, e a ideia era que esse perfil fosse sorteado para um dos seguidores, quando esses fossem em número de um milhão. Agora que essa quantidade de seguidores foi atingida, os organizadores perceberam que apenas 80% deles são realmente fãs do programa. Por conta disso, resolveram que todos os seguidores farão um teste, com perguntas objetivas referentes ao programa, e só poderão participar do sorteio aqueles que forem aprovados. Estatísticas revelam que, num teste dessa natureza, a taxa de aprovação é de 90% dos fãs e de 15% dos que não são fãs.
De acordo com essas informações, a razão entre a probabilidade de que um fã seja sorteado e a probabilidade de que o sorteado seja alguém que não é fã do programa é igual a
fãs do programa = 80% = 0,8 x 1 000 000 = 8 000 000
→ 8 000 000 x 0,9 = 720 000
taxa de aprovação 15% dos que não são fãs: 0,2 x 1 000 000 = 200 000
→ 200 000 x 0,15 = 30 000
Logo,
[tex] razão = \frac{Probabilidade\ de\ que\ um\ fã\ seja\ sorteado}{probabilidade\ de\ que\ o\ sorteado\ seja\ alguém\ que\ não\ é\ fá} [tex]
[tex] razão = \frac{720\ 000}{30\ 000} = 24 [tex]
(ENEM 2017 - 2ª Aplicação).
Ao abrir um negócio, um microempresário descreveu suas vendas, em milhares de reais (unidade monetária brasileira), durante os dois primeiros anos. No primeiro ano, suas vendas cresceram de modo linear. Posteriormente, ele decidiu investir em propaganda, o que fez suas vendas crescerem de modo exponencial.
Qual é o gráfico que melhor descreve as vendas em função do tempo?

Como no primeiro ano, as vendas cresceram de modo linear. E, posteriormente, as vendas cresceram de modo exponencial. Logo, gráfico D.
(ENEM 2017 - 2ª Aplicação).
Em alguns países anglo-saxões, a unidade de volume utilizada para indicar o conteúdo de alguns recipientes é a onça fluida britânica. O volume de uma onça fluida britânica corresponde a 28,4130625 ml.
A título de simplificação, considere uma onça fluida britânica correspondendo a 28 ml.
Nessas condições, o volume de um recipiente com capacidade de 400 onças fluidas britânicas, em cm³, é igual a
1 onça fluida ---------- 28 ml
400 onças ------------- x
x = 400 ∙ 28
x = 11 200
(ENEM 2017 - 2ª Aplicação).
Uma aluna estuda numa turma de 40 alunos. Em um dia, essa turma foi dividida em três salas, A, B e C, de acordo com a capacidade das salas. Na sala A ficaram 1 O alunos, na B, outros 12 alunos e na C, 18 alunos. Será feito um sorteio no qual, primeiro, será sorteada uma sala e, posteriormente, será sorteado um aluno dessa sala.
Qual é a probabilidade de aquela aluna específica ser sorteada, sabendo que ela está na sala C?
[tex] P_{(aluna)} = P_{(sala)} \cdot\ P_{(alunos\ da\ sala\ C)} [tex]
[tex] P_{(aluna)} = \frac{1}{3} \cdot\ \frac{1}{18} [tex]
[tex] P_{(aluna)} = \frac{1}{54} [tex]
(ENEM 2017 - 2ª Aplicação).
Os computadores operam com dados em formato binário (com dois valores possíveis apenas para cada dígito), utilizando potências de 2 para representar quantidades. Assim, tem-se, por exemplo: 1 kB = 210 Bytes, 1 MB = 210 kB e 1 GB = 210 MB, sendo que 210 = 1 024. Nesse caso, tem-se que kB significa quilobyte, MB significa megabyte e GB significa gigabyte. Entretanto, a maioria dos fabricantes de discos rígidos, pendrives ou similares adotam preferencialmente o significado usual desses prefixos, em base 10. Assim, nos produtos desses fabricantes, 1GB = 103 MB = 106 kB = 109 Bytes. Como a maioria dos programas de computadores utilizam as unidades baseadas em potências de 2, um disco informado pelo fabricante como sendo de 80 GB aparecerá aos usuários como possuindo, aproximadamente, 75 GB.
Um disco rígido está sendo vendido como possuindo 500 gigabytes, considerando unidades em potências de 10.
Qual dos valores esta mais próximo do valor informado por um programa que utilize medidas baseadas em potências de 2?
80 GB ---------------- 75 GB
500 GB ---------------- x
[tex] x = \frac{500\ \cdot\ 75}{80} = \frac{37\ 500}{80} = 468,5\ GB [tex]
(ENEM 2017 - 2ª Aplicação).
Chegando ao destino de uma mesma viagem, os turistas X e Y alugarão, cada um deles, um carro. Fizeram, previamente, cotações com as mesmas três locadoras de automóveis da região. Os valores dos aluguéis estão representados pelas expressões dadas no quadro, sendo K o número de quilômetros percorridos, e N o número de diárias pagas pelo aluguel.

O turista X alugará um carro em uma mesma locadora por três dias e percorrerá 250 km. Já a pessoa Y usará o carro por apenas um dia e percorrerá 120 km.
Com o intuito de economizarem com as locações dos carros, e mediante as informações, os turistas X e Y alugarão os carros, respectivamente, nas empresas
Turista X:
Empresa I: P(k) = 100 N + 0,8 k = 100 ∙ 3 + 0,8 ∙ 250 = 300 + 200 = R$ 500,00
Empresa II: P(k) = 70 N + 1,2 k = 70 ∙ 3 + 1,2 ∙ 250 = 210 + 300 = R$ 510,00
Empresa III: P(k) = 120 N + 0,6 k = 120 ∙ 3 + 0,6 ∙ 250 = 360 + 150 = R$ 510,00
Turista Y:
Empresa I: P(k) = 100 N + 0,8 k = 100 ∙ 1 + 0,8 ∙ 120 = 100 + 96 = R$ 196,00
Empresa II: P(k) = 70 N + 1,2 k = 70 ∙ 1 + 1,2 ∙ 120 = 70 + 144 = R$ 214,00
Empresa III: P(k) = 120 N + 0,6 k = 120 ∙ 1 + 0,6 ∙ 120 = 120 + 72 = R$ 192,00
Logo, os turistas X e Y deverão alugar os carros nas empresas I e III, respectivamente.
(ENEM 2017 - 2ª Aplicação).
O governo decidiu reduzir de 25% para 20% o teor de álcool anidro misturado à gasolina vendida nos postos do país. Considere que a média de desempenho, ou seja, a quantidade de quilômetros (km) que um carro anda com 1 litro de combustível, é diretamente proporcional à porcentagem de gasolina presente no combustível, e que a média de desempenho de um carro antes da decisão do governo era de 13,5 km/L.
Nas condições do texto, qual será a estimativa da média de desempenho após a redução de álcool anidro no combustível?
Composição do combustível: 25% álcool anidro + 75 gasolina
Composição do combustível: 20% álcool anidro + 80 gasolina
Como a média é diretamente proporcional a porcentagem de gasolina, temos:
75 % gasolina ------------------- 13,5 km/L
80 % gasolina ---------------- x
[tex] x = \frac{80\ \cdot\ 13,5}{75} = \frac{1080}{75} = 14,4\ km/L [tex]
(ENEM 2017 - 2ª Aplicação).
Numa turma de inclusão de jovens e adultos na educação formal profissional (Proeja), a média aritmética das idades dos seus dez alunos é de 32 anos. Em determinado dia, o aluno mais velho da turma faltou e, com isso, a média aritmética das idades dos nove alunos presentes foi de 30 anos.
Qual é a idade do aluno que faltou naquela turma?
[tex] m = \frac{x_{1}\ +\ ...\ +\ x_{n}}{n} [tex]
[tex] 32 = \frac{x_{1}\ +\ ...\ +\ x_{10}}{10} [tex]
[tex] 320 = x_{1} + ...+x_{10} [tex] (I)
Agora, na falta do aluno mais velho temos:
[tex] 30 = \frac{x_{1}\ +\ ...\ +\ x_{9}}{9} [tex]
[tex] 270 = x_{1}\ +\ ...\ +\ x_{9} [tex] (II)
Por final, subtraindo (I) – (II):
[tex] 320 = x_{1} + ...\ +\ x_{9} +\ x_{10} [tex]
[tex]\underline { 270 = x_{1}\ +\ ...\ +\ x_{9} }[tex]
[tex] 50 = x_{10 }[tex]
Logo, a idade o aluno mais velhos é de 50 anos.
(ENEM 2017 - 2ª Aplicação).
Cinco regiões de um país estão buscando recursos no Governo Federal para diminuir a taxa de desemprego de sua população. Para decidir qual região receberia o recurso, foram colhidas as taxas de desemprego, em porcentagem, dos últimos três anos. Os dados estão apresentados na tabela.

Ficou decidido que a região contemplada com a maior parte do recurso seria aquela com a maior mediana das taxas de desemprego dos últimos três anos.
A região que deve receber a maior parte do recurso é a
Cálculo das medianas - (ordenando as taxas):
Região A: 11,7 - 12,0 - 12,1 → Mediana = 12,0
Região B: 10,5 - 11,6 - 12,5 → Mediana = 11,6
Região C: 10,9 - 11,9 - 12,7 → Mediana = 11,9
Região D: 9,5 - 11,6 - 12,8 → Mediana = 11,6
Região E: 8,2 - 12,6 - 12,7 → Mediana = 12,6
Como a região contemplada será aquela que tiver maior mediana. Logo, é a região E.
(ENEM 2017 - 2ª Aplicação).
Um motorista de um carro flex (bicombustível) calcula que, abastecido com 45 litros de gasolina ou com 60 litros de etanol, o carro percorre a mesma distância.
Chamando de x o valor do litro de gasolina e de y o valor do litro de etanol, a situação em que abastecer com gasolina é economicamente mais vantajosa do que abastecer com etanol é expressa por
x = valor do litro de gasolina
y = valor do litro de álcool
Para que abastecer com gasolina ser mais vantajoso devemos ter:
[tex] 45x < 60y [tex]
[tex] \frac{x}{y} < \frac{60}{45} [tex]
[tex] \frac{x}{y} < \frac{4}{3} [tex]
(ENEM 2017 - 2ª Aplicação).
GH é a sigla que denomina o hormônio do crescimento (do inglês growth hormone), indispensável para retardar o processo de envelhecimento. À medida que envelhecemos, a liberação desse hormônio na corrente sanguínea vai diminuindo. Estudos têm demonstrado, porém, que alguns métodos de treinamento aumentam a produção de GH. Em uma pesquisa, dez homens foram submetidos a sessões de 30 minutos de corrida, em uma esteira, em diferentes intensidades: muito leve, leve, moderada e máxima. As dosagens de GH, medidas por coletas de sangue feitas antes e logo após as sessões, e também 1 hora e 2 horas após o término, são fornecidas no gráfico.

Em qual(is) medição(ões) a liberação de GH na corrente sanguínea em uma sessão de intensidade máxima foi maior que a liberação de GH ocorrida nas demais intensidades?
Nas medições feitas logo após e 1 hora após a sessão de treinamento.
(ENEM 2017 - 2ª Aplicação).
Uma empresa de entregas presta serviços para outras empresas que fabricam e vendem produtos. Os fabricantes dos produtos podem contratar um entre dois planos oferecidos pela empresa que faz as entregas. No plano A, cobra-se uma taxa fixa mensal no valor de R$ 500,00, além de uma tarifa de R$ 4,00 por cada quilograma enviado (para qualquer destino dentro da área de cobertura). No plano B, cobra-se uma taxa fixa mensal no valor de R$ 200,00, porém a tarifa por cada quilograma enviado sobe para R$ 6,00. Certo fabricante havia decidido contratar o plano A por um período de 6 meses. Contudo, ao perceber que ele precisará enviar apenas 650 quilogramas de mercadoria durante todo o período, ele resolveu contratar o plano B.
Qual alternativa avalia corretamente a decisão final do fabricante de contratar o plano B?
Plano A: P(k) = 6 ∙ 500 + 4k
Plano B: P(k) = 6 ∙ 200 + 6k
Plano A: P(k) = 6 ∙ 500 + 4 ∙ 650 = 3 000 + 2600 = R$ 5 600,00
Plano B: P(k) = 6 ∙ 200 + 6 ∙ 650 = 1200 + 3 900 = R$ 5 100,00
Logo,
R$ 5 600,00 – R$ 5 100,00 = R$ 500,00
(ENEM 2017 - 2ª Aplicação).
Duas amigas irão fazer um curso no exterior durante 60 dias e usarão a mesma marca de xampu. Uma delas gasta um frasco desse xampu em 10 dias enquanto que a outra leva 20 dias para gastar um frasco com o mesmo volume. Elas combinam de usar, conjuntamente, cada frasco de xampu que levarem.
O número mínimo de frascos de xampu que deverão levar nessa viagem é
Tempo: 60 dias
Amiga I: 10 dias
Amiga II: 20 dias
Amiga I: [tex] \frac{60}{10} = 6\ frascos [tex]
Amiga II: [tex] \frac{60}{20} = 3\ frascos [tex]
Conjuntamente: 6 + 3 frascos = 9 frascos
(ENEM 2017 - 2ª Aplicação).
No centro de uma praça será construída uma estátua que ocupará um terreno quadrado com área de 9 metros quadrados. O executor da obra percebeu que a escala do desenho na planta baixa do projeto é de 1 : 25.
Na planta baixa, a área da figura que representa esse terreno, em centímetro quadrado, é
Terreno quadrado: 9 m² → lado = 3 m
escala: 1 : 25
1 cm ----------- 25 cm
x cm ------------ 300 cm (3m)
[tex] x = \frac{300}{25} = 12\ cm [tex]
Assim, na planta baixa a área da figura é:
A = 12 x 12
A = 144 cm²
(ENEM 2017 - 2ª Aplicação).
Uma indústria tem um setor totalmente automatizado. São quatro máquinas iguais, que trabalham simultânea e ininterruptamente durante uma jornada de 6 horas. Após esse período, as máquinas são desligadas por 30 minutos para manutenção. Se alguma máquina precisar de mais manutenção, ficará parada até a próxima manutenção.
Certo dia, era necessário que as quatro máquinas produzissem um total de 9 000 itens. O trabalho começou a ser feito às 8 horas. Durante uma jornada de 6 horas, produziram 6 000 itens, mas na manutenção observou-se que uma máquina precisava ficar parada. Quando o serviço foi finalizado, as três máquinas que continuaram operando passaram por uma nova manutenção, chamada manutenção de esgotamento.
Em que horário começou a manutenção de esgotamento?
máquinas: 4
jornada: 6 horas
tempo de manutenção: 30 min = 0,5 horas
[tex] \frac{3000}{3} = 1000 [tex]início da jornada: 8:00h
Como na jornada de 6 horas produziram 6000 itens, restando: 9000 – 6 000 = 3000 itens.
Também, cada máquina produz: [tex] \frac{6000}{4} = 1500 [tex] itens por jornada → [tex] \frac{1500}{6} = 250 [tex] itens/hora
Como uma máquina teve que ficar parada. Logo, o restante
[tex] \frac{3000}{3} = 1000 [tex] itens por máquina → [tex] \frac{1000\ itens}{250} = 4\ horas [tex]
Logo, 8:00h + 6h = 14:00 + 4h
= 18:00h + 30 minutos (para iniciar a manutenção)
= 18 h 30 minutos
(ENEM 2017 - 2ª Aplicação).
Desde 1999 houve uma significativa mudança nas placas dos carros particulares em todo o Brasil. As placas, que antes eram formadas apenas por seis caracteres alfanuméricos, foram acrescidas de uma letra, passando a ser formadas por sete caracteres, sendo que os três primeiros caracteres devem ser letras (dentre as 26 letras do alfabeto) e os quatro últimos devem ser algarismos (de O a 9). Essa mudança possibilitou a criação de um cadastro nacional unificado de todos os veículos licenciados e ainda aumentou significativamente a quantidade de combinações possíveis de placas. Não são utilizadas placas em que todos os algarismos sejam iguais a zero.
Disponível em: http://gl.globo.com. Acesso em: 14 jan. 2012 (adaptado).
Nessas condições, a quantidade de placas que podem ser utilizadas é igual a
Letra: L
número: N
L L L N N N N
↓ ↓ ↓ ↓ ↓ ↓ ↓
26 26 26 10 10 10 10
Lembrando que não é considerado a placa L L L 0 0 0 0.
Logo, [tex] 26³ \cdot\ (10^{4} – 1) [tex]
(ENEM 2017 - 2ª Aplicação).
A figura traz o esboço da planta baixa de uma residência. Algumas medidas internas dos cômodos estão indicadas. A espessura de cada parede externa da casa é 0,20 m e das paredes internas, 0,10 m.

Sabe-se que, na localidade onde se encontra esse imóvel, o Imposto Predial Territorial Urbano (IPTU) é calculado conforme a área construída da residência. Nesse cálculo, são cobrados R$ 4,00 por cada metro quadrado de área construída.
O valor do IPTU desse imóvel, em real, é
Cálculo da área da planta baixa:
A = base x altura = (0,20 + 3 + 0,10 + 3 + 0,20) × (0,20 + 4 + 0,10 + 2 + 0,10 + 4,4 + 0,20)
A = 6,5 x 11,0
A = 71,5 m²
Agora, encontrar o IPTU.
1 m² ------------ R$ 4,00
71,5 m² --------- x
x = 71,5 x 4,00 = R$ 286,00
(ENEM 2017 - 2ª Aplicação).
Uma televisão pode ser posicionada de modo que se consiga enxergar os detalhes de uma imagem em alta definição. Considere que a distância ideal, com conforto visual, para se assistir à televisão de 32 polegadas é de 1,8 metro. Suponha que haja uma relação de proporcionalidade direta entre o tamanho da tela (medido em polegada) e a distância ideal. Considere que um espectador dispõe de uma televisão de 60 polegadas e que ele deseja se posicionar em frente a ela, com conforto visual.
A distância da televisão, em metro, em que o espectador deve se posicionar para que tenha conforto visual é mais próxima de
32'' ------------ 1,8 m
60'' ------------ x
[tex] x = \frac{60\ \cdot\ 1,8}{32} = \frac{108}{32} = 3,375 [tex]
(ENEM 2017 - 2ª Aplicação).
No primeiro ano do ensino médio de uma escola, é hábito os alunos dançarem quadrilha na festa junina. Neste ano, há 12 meninas e 13 meninos na turma, e para a quadrilha foram formados 12 pares distintos, com postos por uma menina e um menino. Considere que as meninas sejam os elementos que compõem o conjunto A e os meninos, o conjunto B, de modo que os pares formados representem uma função f de A em B.
Com base nessas informações, a classificação do tipo de função que está presente nessa relação é
A relação f é injetora, pois para cada menina pertencente ao conjunto A está associado um menino diferente pertencente ao conjunto B.
(ENEM 2017 - 2ª Aplicação).
Um funcionário da Secretaria de Meio Ambiente de um município resolve apresentar ao prefeito um plano de priorização para a limpeza das lagoas da cidade. Para a execução desse plano, o prefeito decide voltar suas ações, primeiramente, para aquela lagoa que tiver o maior coeficiente de impacto, o qual é definido como o produto entre o nível de contaminação médio por mercúrio em peixes e o tamanho da população ribeirinha. O quadro mostra as lagoas do município e suas correspondentes informações.

A primeira lagoa que sofrerá a intervenção planejada será a
coeficiente de impacto = (nível de contaminação médio por mercúrio em peixes) × (tamanho da população ribeirinha)
Antiga: coeficiente = 2,1 × 1522 = 3 196,2
Bela: coeficiente = 3,4 × 2508 = 8 527,2
Delícia: coeficiente = 42,9 × 2476 = 106 220,4
Salgada: coeficiente = 53,9 × 2455 = 132 324,5
Vermelha: coeficiente = 61,4 × 145 = 8 903
(ENEM 2017 - 2ª Aplicação).
Para a Olimpíada de 2012, a piscina principal do Centro Aquático de Londres, medindo 50 metros de comprimento, foi remodelada para ajudar os atletas a melhorar suas marcas. Observe duas das melhorias:

Veja, n. 2 278, jul. 2012 (adaptado).
A capacidade da piscina em destaque, em metro cúbico, é igual a
Capacidade = V = comprimento × largura × altura
V = 50m × (10 × 2,5)m × 3 m
V = 50 × 25 × 3
V = 3 750 m³
(ENEM 2017 - 2ª Aplicação).
Um fabricante recomenda que, para cada m2 do ambiente a ser climatizado, são necessários 800 BTUh, desde que haja até duas pessoas no ambiente. A esse número devem ser acrescentados 600 BTUh para cada pessoa a mais, e também para cada aparelho eletrônico emissor de calor no ambiente. A seguir encontram-se as cinco opções de aparelhos desse fabricante e suas respectivas capacidades térmicas:

O supervisor de um laboratório precisa comprar um aparelho para climatizar o ambiente. Nele ficarão duas pessoas mais uma centrífuga que emite calor. O laboratório tem forma de trapézio retângulo, com as medidas apresentadas na figura.
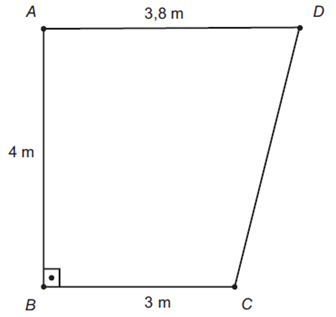
Para economizar energia, o supervisor deverá escolher o aparelho de menor capacidade térmica que atenda às necessidades do laboratório e às recomendações do fabricante.
A escolha do supervisor recairá sobre o aparelho do tipo
Área do laboratório:
A = [tex] \frac{(B\ +\ b)h}{2} = \frac{(3,8\ +\ 3)4}{2} = 6,8\ \cdot\ 2 = 13,6\ m² [tex]
Tipo I: 13,6 x 800 BTBh + 600 BTUh = 10 880 + 600 = 11 480 BTUh
Logo, deve-se escolher o aparelho III.
(ENEM 2017 - 2ª Aplicação).
Os consumidores X, Y e Z desejam trocar seus planos de internet móvel na tentativa de obterem um serviço de melhor qualidade. Após pesquisarem, escolheram uma operadora que oferece cinco planos para diferentes perfis, conforme apresentado no quadro.

Em cada plano, o consumidor paga um valor fixo (preço mensal da assinatura) pela franquia contratada e um valor variável, que depende da quantidade de MB utilizado além da franquia. Considere que a velocidade máxima de acesso seja a mesma, independentemente do plano, que os consumos mensais de X, Y e Z são de 190 MB, 450 MB e 890 MB, respectivamente, e que cada um deles escolherá apenas um plano.
Com base nos dados do quadro, as escolhas dos planos com menores custos para os consumidores X, Y e Z, respectivamente, são
plano X: 190 MB
plano Y: 450 MB
plano Z: 890 MB
CONSUMIDOR X (190 MB):
Plano A: R$ 29,90 + (R$ 0,40 x 40) = R$ 29,90 + R$ 16,00 = R$ 45,90
Plano B: R$ 34,90 + (R$ 0,10 x 60) = R$ 34,90 + R$ 6,00 = R$ 40,90
Plano C: R$ 59,90 + (R$ 0,10 x 310) = R$ 59,90 + R$ 31,00 = R$ 90,90
CONSUMIDOR Y (450 MB):
Plano A: R$ 29,90 + (R$ 0,40 x 260) = R$ 29,90 + R$ 104,00 = R$ 133,90
Plano B: R$ 34,90 + (R$ 0,10 x 200) = R$ 34,90 + R$ 20,00 = R$ 54,90
Plano C: R$ 59,90 + (R$ 0,10 x 50) = R$ 59,90 + R$ 5,00 = R$ 64,90
Plano D: R$ 89,90 + (R$ 0,10 x 1550) = R$ 59,90 + R$ 115,00 = R$ 244,90
CONSUMIDOR Z (890 MB):
Plano A: Plano insuficiente
Plano B: Plano insuficiente
Plano C: Plano insuficiente
Plano D: R$ 89,90 + (R$ 0,10 x 1110) = R$ 99,90 + R$ 110,00 = R$ 244,90
Plano E: R$ 119,90 + (R$ 0,10 x 4110) = R$ 99,90 + R$ 410,00 = R$ 530,00.
(ENEM 2017 - 2ª Aplicação).
Uma lagartixa está no interior de um quarto e começa a se deslocar. Esse quarto, apresentando o formato de um paralelepípedo retangular, é representado pela figura.

A lagartixa parte do ponto B e vai até o ponto A. A seguir, de A ela se desloca, pela parede, até o ponto M, que é o ponto médio do segmento EF. Finalmente, pelo teto, ela vai do ponto M até o ponto H. Considere que todos esses deslocamentos foram feitos pelo caminho de menor distância entre os respectivos pontos envolvidos.
A projeção ortogonal desses deslocamentos no plano que contém o chão do quarto é dado por:
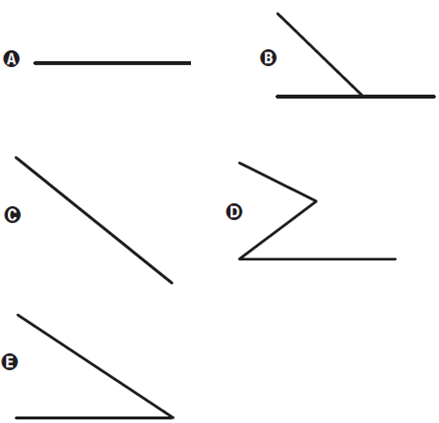
(ENEM 2017 - 2ª Aplicação).
Em um mês, uma loja de eletrônicos começa a obter lucro já na primeira semana. O gráfico representa o lucro ( L ) dessa loja desde o início do mês até o dia 20. Mas esse comportamento se estende até o último dia, o dia 30.

A representação algébrica do lucro ( L ) em função do tempo (t) é
[tex]L(t) = at + b [tex]
b = – 1000
a = ?
Calculo do coeficiente angular "a":
[tex] a = \frac{Δy}{Δx} = \frac{3000 - (-1000)}{20-0} = \frac{4000}{20} = 200 [tex]
Logo,
[tex] L(t) = at + b [tex]
[tex] L(t) = 200t – 1000 [tex]
(ENEM 2017 - 2ª Aplicação).
O gráfico mostra a expansão da base de assinantes de telefonia celular no Brasil, em milhões de unidades, no período de 2006 a 2011.

De acordo com o gráfico, a taxa de crescimento do número de aparelhos celulares no Brasil, de 2007 para 2011, foi de
120,98 ---------- 100%
224,02 ---------- x %
[tex] x = \frac{224,02\ \cdot\ 100}{120,98} = \frac{22402}{120,98} = 185,17\ % [tex]
Logo, a taxa de crescimento é:
185,17% = 100% + 85,17 %
(ENEM 2017 - 2ª Aplicação).
O estado de qualquer substância gasosa é determinado pela medida de três grandezas: o volume (V), a pressão (P) e a temperatura ( T ) dessa substância. Para os chamados gases "ideais", o valor do quociente PV/T é sempre constante. Considere um reservatório que está cheio de um gás ideal. Sem vazar o gás, realiza-se uma compressão do reservatório, reduzindo seu volume à metade. Ao mesmo tempo, uma fonte de calor faz a temperatura do gás ser quadruplicada. Considere Po e P1 respectivamente, os valores da pressão do gás no reservatório, antes e depois do procedimento descrito.
A relação entre Po e P1 é
[tex] \frac{P_{0}\ \cdot\ V_{0}}{ T_{0}} = \frac{P_{1}\ \cdot\ V_{1}}{ T_{1}} [tex]
[tex] \frac{P_{0}\ \cdot\ V_{0}}{ T_{0}} = \frac{P_{1}\ \cdot\ \frac{ V_{0}}{2}}{ T_{1}} [tex]
[tex] P_{1}\ \cdot\ \frac{ V_{0}}{2}\ \cdot\ T_{0} = P_{0}\ \cdot\ V_{0} \ \cdot\ 4T_{0} [tex]
[tex] P_{1} = \frac{P_{0}\ \cdot\ V_{0} \ \cdot\ 4T_{0}} {\frac{ V_{0}}{2}\ \cdot\ T_{0}} [tex]
[tex] P_{1} = \frac{{P_{0}\ \cdot\ 4}}{ \frac{1}{2}} [tex]
[tex] P_{1} = P_{0}\ \cdot\ 4\ \cdot\ 2[tex]
[tex] P_{1} = 8 P_{0} [tex]
(ENEM 2017 - 2ª Aplicação).
Uma repartição pública possui um sistema que armazena em seu banco de dados todos os ofícios, memorandos e cartas enviados ao longo dos anos. Para organizar todo esse material e facilitar a localização no sistema, o computador utilizado pela repartição gera um código para cada documento, de forma que os oito primeiros dígitos indicam a data em que o documento foi emitido (DDMMAAAA), os dois dígitos seguintes indicam o tipo de documento (ofício: 01, memorando: 02 e carta: 03) e os três últimos dígitos indicam a ordem do documento. Por exemplo, o código 0703201201003 indica um ofício emitido no dia 7 de março de 2012, cuja ordem é 003. No dia 27 de janeiro de 2001, essa repartição pública emitiu o memorando de ordem 012 e o enviou aos seus funcionários.
O código gerado para esse memorando foi
1°: 8 primeiros dígitos indicam a data em que o documento foi emitido (DDMMAAAA);
2°: 2 dígitos seguintes indicam o tipo de documento;
3°: 3 últimos dígitos indicam a ordem do documento.
Logo,
• 27 de janeiro de 2001: 27012001
• essa repartição pública emitiu o memorando: 02
• de ordem 012: 012
Assim, o código gerado é:
2701200102012
(ENEM 2017 - 2ª Aplicação).
A baixa procura por carne bovina e o aumento de oferta de animais para abate fizeram com que o preço da arroba do boi apresentasse queda para o consumidor. No ano de 2012, o preço da arroba do boi caiu de R$ 100,00 para R$ 93,00.
Disponível em: www.diariodemarilia.com.br. Acesso em: 14 ago. 2012.
Com o mesmo valor destinado a aquisição de carne, em termos de perda ou ganho, o consumidor
93,00 ------------- 100%
7,00 -------------- x %
[tex] x = \frac{-7\ \cdot\ 100}{93} = \frac{700}{93} = 7,52\ % [tex]
(ENEM 2017 - 2ª Aplicação).
Uma pessoa encheu o cartão de memória de sua câmera duas vezes, somente com vídeos e fotos. Na primeira vez, conseguiu armazenar 10 minutos de vídeo e 190 fotos. Já na segunda, foi possível realizar 15 minutos de vídeo e tirar 150 fotos. Todos os vídeos possuem a mesma qualidade de imagem entre si, assim como todas as fotos. Agora, essa pessoa deseja armazenar nesse cartão de memória exclusivamente fotos, com a mesma qualidade das anteriores.
Disponível em: www.techlider.com.br. Acesso em: 31 jul. 2012.
O número máximo de fotos que ela poderá armazenar é
1ª vez: 10 minutos de vídeo e 190 fotos
2ª vez: 15 minutos de vídeo e tirar 150 fotos
(15 ¬– 10) minutos = 190 – 150 =
5 minutos = 40 fotos
1 minuto = 8 fotos
Logo,
10 minutos de vídeo e 190 fotos =
10 x 8 fotos + 190 fotos
80 fotos + 190 fotos =
270 fotos
(ENEM 2017 - 2ª Aplicação).
As empresas que possuem Serviço de Atendimento ao Cliente (SAC), em geral, informam ao cliente que utiliza o serviço um número de protocolo de atendimento. Esse número resguarda o cliente para eventuais reclamações e é gerado, consecutivamente, de acordo com os atendimentos executados. Ao término do mês de janeiro de 2012, uma empresa registrou como último número de protocolo do SAC o 390 978 467. Do início do mês de fevereiro até o fim do mês de dezembro de 2012, foram abertos 22 580 novos números de protocolos.
O algarismo que aparece na posição da dezena de milhar do último número de protocolo de atendimento registrado em 2012 pela empresa é
• janeiro de 2012: 390 978 467
• dezembro de 2012:
390 978 467 + 22 580 = 391 001 047
Logo, o algarismo que aparece na posição da dezena de milhar é 0.
(ENEM 2017 - 2ª Aplicação).
Nas informações veiculadas nos órgãos de comunicação quando da ocorrência de um terremoto, faz-se referência à magnitude ( M ), que se refere a quantos graus o fenômeno atingiu na escala Richter. Essa medida quantifica a energia liberada no epicentro do terremoto, e em seu cálculo utilizam-se como parâmetros as medidas da amplitude sísmica ( A ), em micrômetro, e da frequência (f), em hertz. Esses parâmetros são medidos por aparelhos especiais chamados sismógrafos, e relacionam-se segundo a função M = log (A x f) + 3,3. Pela magnitude do terremoto na escala Richter, pode-se estimar seus efeitos de acordo com o quadro, onde não estão considerados terremotos de magnitudes superiores a 7 ,9.

Um terremoto teve sua amplitude e frequências medidas e obteve-se A = 1 000 micrômetros e f = 0,2 hertz.
Use – 0,7 como aproximação para log(0,2).
Disponível em: www.mundoeducacao.com.br. Acesso em: 11 jul. 2012 (adaptado).
Considerando o quadro apresentado, e analisando o resultado da expressão que fornece a magnitude desse terremoto, conclui-se que ele foi
M = log (A × f) + 3,3
M = log (1 000 × 0,2) + 3,3
M = log (200) + 3,3
M = log (0,2 × 10³) + 3,3
M = log (0,2) + log(10³) + 3,3
M = – 0,7 + 3 + 3,3
M = – 0,7 + 6,3
M = + 5,6
Assim, de acordo com a tabela, temos: destrutivo, com consequências significativas em edificações pouco estruturadas.
(ENEM 2017 - 2ª Aplicação).
Uma pessoa pede informação na recepção de um prédio comercial de como chegar a uma sala, e recebe as seguintes instruções: suba a escada em forma de U à frente, ao final dela vire à esquerda, siga um pouco à frente e em seguida vire à direita e siga pelo corredor. Ao final do corredor, vire à direita.
Uma possível projeção vertical dessa trajetória no plano da base do prédio é:
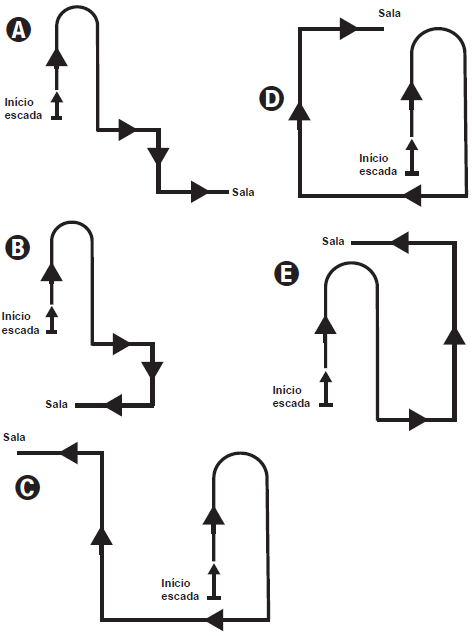
(ENEM 2017 - 2ª Aplicação).
Um dos principais indicadores de inflação é o Índice Nacional de Preços ao Consumidor Amplo (IPCA). O gráfico apresenta os valores do IPCA nos anos de 1994 a 2011.

O valor mais próximo da mediana de todos os valores da inflação indicados no gráfico é
Ordenando os valores:
1,65 - 3,14 - 4,31 - 4,46 - 5,22 - 5,69 - 5,90 - 5,91 - 5,97 - 6,50 - 7,60 - 7,67 - 8,94 - 9,30 - 9,56 - 12,53 - 18,57 - 22,41
[tex] Me = \frac{5,97\ +\ 6,50}{2} = \frac{12,47}{2} = 6,235 [tex]
(ENEM 2017 - 2ª Aplicação).
Uma equipe de ambientalistas apresentou um mapa de uma reserva ambiental em que faltava a especificação da escala utilizada para a sua confecção. O problema foi resolvido, pois um dos integrantes da equipe lembrava-se de que a distância real de 72 km, percorrida na reserva, equivalia a 3,6 cm no mapa.
Qual foi a escala utilizada na confecção do mapa?
mapa real
3,6 cm ---------- (7 200 000 cm) 72 km
x cm ---------- 1 cm
[tex] x = \frac{3,6}{7\ 200\ 000} = \frac{3,6\ \cdot\ 10}{7\ 200\ 000\ \cdot\ 10} = \frac{36}{72\ 000\ 000} [tex]
[tex] = \frac{36\ :\ 36}{72\ 000\ 000\ :\ 36} = \frac{1}{2\ 000\ 000} [tex]
Logo, a escala é 1 : 2 000 000.

Nenhum comentário:
Postar um comentário