(ENEM 2021 - 2ª Aplicação).
Na loteria Lotex, cada aposta corresponde à marcação de cinquenta números em um cartão. Caso o apostador marque uma quantidade inferior a cinquenta números, o sistema completará aleatoriamente a sua aposta até integralizar os cinquenta números necessários. Por exemplo, o cartão de aposta retratado representa as escolhas de um jogador antes que o sistema integralize o seu preenchimento.

Com relação ao cartão exibido, o jogador reconhece que o número racional que corresponde ao quociente do número de pontos marcados pelo sistema, em seu jogo, pelo número máximo de pontos para validar a aposta é igual a
O número racional que corresponde ao quociente do número de pontos marcados pelo sistema, em seu jogo, pelo número máximo de pontos para validar a aposta é igual a:
[tex]P = \frac{Pontos\ marcados\ pelo\ sistema}{Número\ máximo\ de\ pontos} [tex]
[tex]P = \frac{50\ -\ 22}{50} = \frac{28}{50} = \frac{14}{25} [tex]
Portanto, alternativa "B".
(Créditos da resolução: Prof. Warles)
(ENEM 2021 - 2ª Aplicação).
A imagem representa uma calculadora científica com duas teclas destacadas. A tecla A eleva ao quadrado o número que está no visor da calculadora, e a tecla B extrai a raiz cúbica do número apresentado no visor.

Uma pessoa digitou o número 8 na calculadora e em seguida apertou três vezes a tecla A e depois uma vez a tecla B. A expressão que representa corretamente o cálculo efetuado na calculadora é
Vejas as etapas:
• Uma pessoa digitou o número 8 na calculadora: [tex] 8 [tex]
• em seguida, apertou a tecla A: [tex] 8^{2} [tex]
• apertou a tecla A: [tex] (8^{2})^2 [tex]
• apertou a tecla A: [tex] ((8^{2})^2)^2 = 8^{2\ \cdot\ 2\ \cdot\ 2} [tex]
• e depois uma vez a tecla B.
[tex] \sqrt[3]{8^{2\ \cdot\ 2\ \cdot\ 2}} [tex]
Portanto, alternativa "B".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Uma rede de supermercados vende latas de sucos em packs (pacotes) com 12 latas. A venda é feita da seguinte forma:
• um pack é vendido por R$ 21,60;
• na compra de dois packs, o segundo tem 40% de desconto sobre o seu valor.
Entretanto, essa rede de supermercados costuma disponibilizar também o valor unitário do produto em cada uma das situações de compra. Para obter esse valor, basta dividir o total gasto pela quantidade de latas adquiridas. Em determinado dia, nos cinco supermercados da rede que vendem os packs da forma descrita, os registros do valor unitário da lata de suco para o cliente que comprava dois packs eram diferentes entre si, conforme os dados:
Loja I: R$ 1,08;
Loja II: R$ 1,40;
Loja III: R$ 1,44;
Loja IV: R$ 1,76;
Loja V: R$ 1,78.
Em um dos supermercados, o valor unitário está correto, de acordo com o costume da rede ao vender dois packs. Esse supermercado corresponde à loja
Quando um cliente compra 2 packs, então ele paga R$ 21,60 no primeiro e (100% – 40% = 60% = 0,60) de R$ 21,60 no segundo pack. Logo:
[tex] = 21,60 × 0,60 [tex]
[tex] = R \$\ 12,96 [tex]
Então, ao comprar os 2 packs o cliente deve pagar:
= Valor do 1º packs + Valor do 2ª packs
[tex] = 21,60 + 12,96 [tex]
[tex] = R \$\ 34,56 [tex]
Sabemos também que cada pack tem 12 latas, então 2 packs possuem:
[tex] = 2 × 12 = 24\ latas[tex]
O preço de cada lata é de:
[tex]= \frac{R \$\ 34,56}{24} [tex]
[tex] = R \$\ 1,44 [tex]
Podemos concluir que a única loja que está informando o valor correto do preço por lata é a Loja III: R$ 1,44;
Portanto, alternativa "C".
(Créditos da resolução: Prof. Warles)
(ENEM 2021 - 2ª Aplicação).
Um fabricante produz cinco tipos de enfeites de Natal. Para saber o lucro líquido correspondente a cada tipo de enfeite, criou um quadro com os valores de custo (matéria-prima e mão de obra) e de venda por unidade, em real, além da quantidade vendida para cada tipo de enfeite.
| Tipo | Matéria- -prima (R$) | Mão de obra (R$) | valor de venda (R) | Quantidade vendida |
|---|---|---|---|---|
| I | 1,30 | 1,50 | 5,00 | 5 000 |
| II | 1,00 | 2,00 | 5,50 | 4 800 |
| III | 1,10 | 1,40 | 5,00 | 4 700 |
| IV | 1,50 | 2,00 | 7,00 | 4 600 |
| V | 1,20 | 2,50 | 7,50 | 4 200 |
Qual tipo de enfeite de Natal gera maior lucro líquido para o fabricante?
O tipo de enfeite de Natal que gera maior lucro líquido para o fabricante é o:
[tex] = 5\ 000 × (5,00 - (1,30 + 1,50)) [tex]
[tex] = 5\ 000 × 2,20 [tex]
[tex] = R \$\ 11\ 000 [tex]
[tex] = 4\ 800 × (5,50 - (1,00 + 2,00)) [tex]
[tex] = 4\ 800 × 2,50 [tex]
[tex] = R \$\ 12\ 000 [tex]
[tex] = 4\ 750 × (5,00 - (1,10 + 1,40)) [tex]
[tex] = 4\ 750 × 2,50 [tex]
[tex] = R \$\ 11\ 875 [tex]
[tex] = 4\ 600 × (7,00 - (1,50 + 2,00)) [tex]
[tex] = 4\ 600 × 3,50 [tex]
[tex] = \color{blue}{R \$\ 16\ 100} [tex]
[tex] = 4\ 200 × (7,50 - (1,20 + 2,50)) [tex]
[tex] = 4\ 200 × 3,70 [tex]
[tex] = R \$\ 15\ 540 [tex]
Portanto, alternativa "D".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Em determinado mês, o consumo de energia elétrica da residência de uma família foi de 400 kWh. Achando que o valor da conta estava alto, os membros da família decidiram diminuí-lo e estabeleceram a meta de reduzir o consumo em 40%. Começaram trocando a geladeira, de consumo mensal igual a 90 kWh, por outra, de consumo mensal igual a 54 kWh, e realizaram algumas mudanças na rotina de casa:
• reduzir o tempo de banho dos moradores, economizando 30 kWh por mês;
• reduzir o tempo em que o ferro de passar roupas fica ligado, economizando 14 kWh por mês;
• diminuir a quantidade de lâmpadas acesas no período da noite, conseguindo uma redução de 10 kWh mensais.
No entanto, observaram que, mesmo assim, não atingiriam a meta estabelecida e precisariam decidir outras maneiras para diminuir o consumo de energia.
De modo a atingir essa meta, o consumo mensal de energia, em quilowatt-hora, ainda precisa diminuir
Primeiro encontrar a meta de redução de consumo de luz por mês, sabendo que precisa reduzir 40%:
= 40% × 400 kWh
= 0,40 × 400 kWh
= 160 kWh
Agora, encontrar a economia com a troca da geladeira:
= 90 kWh – 54 kWh
= 36 kWh
Encontrar a soma de todas as economias do mês:
= 36 + 30 + 14 + 10
= 90 kWh
Como a meta é reduzir 160 kWh e, já conseguiu reduzir 90 kWh. Dessa forma, ainda precisa reduzir:
= 160 – 9 0 = 70 kWh
Portanto, alternativa "E".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Um inseto percorreu sobre a superfície de um objeto, em formato de um prisma reto ABCDEFGH, com base retangular, uma trajetória poligonal, com vértices nos pontos: A - X - Y - G - F - E - X - G - E, na ordem em que foram apresentados.
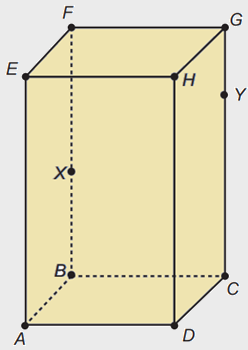
É necessário representar a projeção ortogonal do trajeto percorrido pelo inseto sobre o plano determinado pela base do prisma.
A representação da projeção ortogonal do trajeto percorrido pelo inseto é

A projeção ortogonal pode associada a sombra do inseto na base do prisma. Logo:
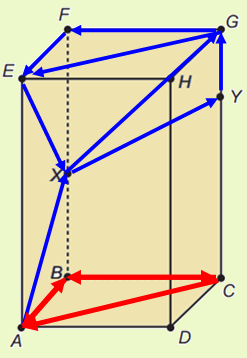
Portanto, alternativa "D".
(Créditos da resolução: Curso Objetivo)
(ENEM 2021 - 2ª Aplicação).
Uma moça estacionou seu carro na interseção da Rua 1 com a Avenida A. Ela está hospedada em um hotel na Rua 3, posicionado a exatos 40 metros de distância da Avenida A, contados a partir da Avenida A em direção à Avenida B. No mapa está representado um plano cartesiano cujo eixo das abscissas coincide com a Avenida A e o das ordenadas, com a Rua 1, sendo a origem (0, 0) o local onde se encontra estacionado o veículo. Os quarteirões formados pelos cruzamentos dessas vias formam quadrados de lados medindo 100 m.
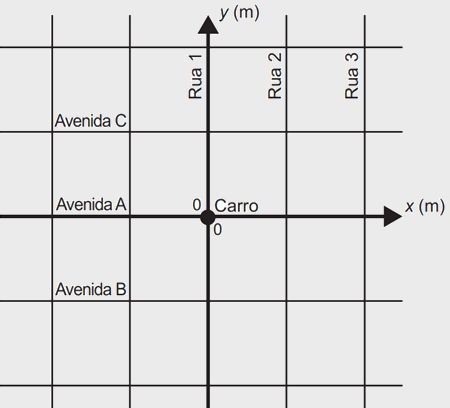
A ordenada do ponto que representa a localização do hotel é
Observe a figura a seguir:
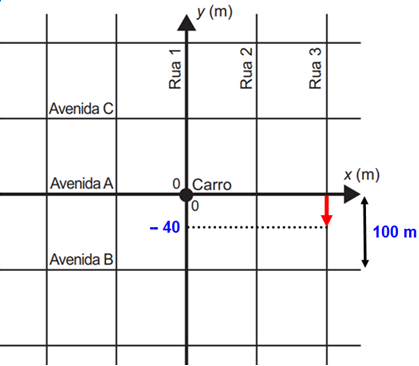
Portanto, alternativa "B".
(Créditos da resolução: Prof. Warles)
(ENEM 2021 - 2ª Aplicação).
Um brinquedo muito comum em parques de diversões é o balanço. O assento de um balanço fica a uma altura de meio metro do chão, quando não está em uso. Cada uma das correntes que o sustenta tem medida do comprimento, em metro, indicada por x. A estrutura do balanço é feita com barras de ferro, nas dimensões, em metro, conforme a figura.
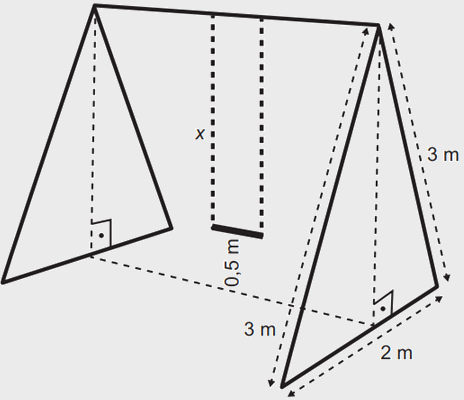
Nessas condições, o valor, em metro, de [tex]x[tex] é igual a
Observe a figura a seguir:

Aplicando o Teorema de Pitágoras, no triângulo em vermelho, para encontrar o valor de [tex]y[tex]:
[tex] a^{2} = b^{2} + c^{2}[tex]
[tex] 3^{2} = y^{2} + 1^{2}[tex]
[tex] 9 = y^{2} + 1[tex]
[tex] 9 - 1 = y^{2}[tex]
[tex] 8 = y^{2}[tex]
[tex] y = \sqrt{8}[tex]
Agora, encontrar o valor de x:
[tex] x = y - 0,5[tex]
[tex] x = \sqrt{8} - 0,5[tex]
Portanto, alternativa "C".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Uma indústria recortou uma placa de metal no formato triangular ABC, conforme Figura 1, com lados 18, 14 e 12 cm.
Posteriormente, a peça triangular ABC foi dobrada, de tal maneira que o vértice B ficou sobre o segmento AC, e o segmento DE ficou paralelo ao lado AC, conforme figura 2.

Sabe-se que, na Figura 1, o ângulo ACB é menor que o ângulo CAB e este é menor que o ângulo ABC, e que os cortes e dobraduras foram executados corretamente pelas máquinas.
Nessas condições, qual é o valor da soma dos comprimentos, em centímetro, dos segmentos DB, BE e EC?
Em primeiro lugar, encontrar os valores de AB, AC e BC.
“o ângulo [tex]A\hat{C}B[tex] é menor que o ângulo [tex]C\hat{A}B[tex] e este é menor que o ângulo [tex]A\hat{B}C[tex]”
[tex]A\hat{C}B < C\hat{A}B < A\hat{B}C [tex]
Ou seja, em triângulo o menor ângulo está oposto ao menor lado. Também, o maior ângulo é oposto ao maior lado. Logo:

Como a indústria vai dobrar o triângulo levando o ponto B até o ponto que ilustramos a seguir como B'. Fazendo isso o segmento DE fica paralelo a AC.

O objetivo da questão é obter [tex]DB + BE + EC[tex]. Já sabemos quanto vale [tex]BE + EC = BC = 14\ cm[tex].
A indústria ao criar essa dobra, criou triângulos semelhantes:
[tex] ABB'\ \sim\ DBF [tex]
Além disso, sabemos que:
[tex] BF = FB' = h [tex]
Dessa forma:
[tex] \frac{12}{x} = \frac{h + h}{h} [tex]
[tex] \frac{12}{x} = \frac{2h}{h} [tex]
[tex] \frac{12}{x} = \frac{2}{1} [tex]
[tex] 2x = 12 [tex]
[tex] x = 6 [tex]
Por último,
[tex] = BD + AD [tex]
[tex] = x + 14\ cm [tex]
[tex] = 6\ cm + 14\ cm [tex]
[tex]= 20\ cm [tex]
Portanto, alternativa "B".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Um suporte será instalado no box de um banheiro para serem colocados recipientes de xampu, condicionador e sabonete líquido, sendo que o recipiente de cada produto tem a forma de um cilindro circular reto de medida do raio igual a 3 cm. Para maior conforto no interior do box, a proprietária do apartamento decidiu comprar o suporte que tiver a base de menor área, desde que a base de cada recipiente ficasse inteiramente sobre o suporte.
Nas figuras, vemos as bases desses suportes, nas quais todas as medidas indicadas estão em centímetro.
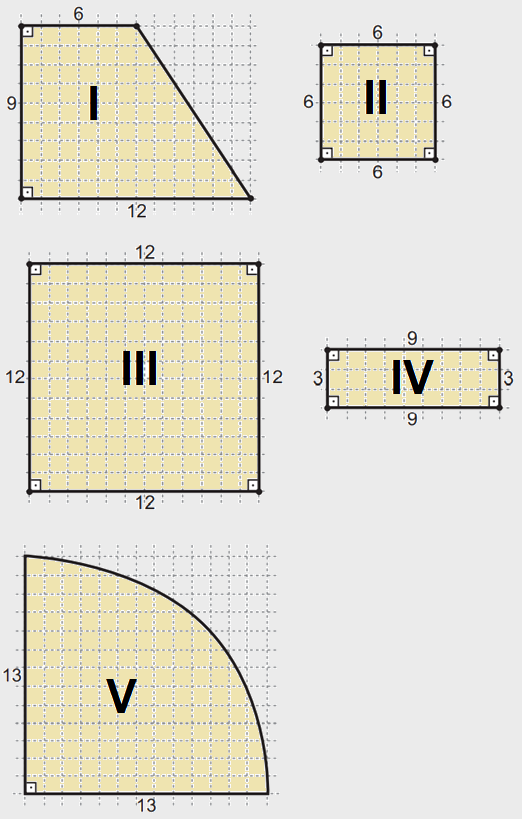
Utilize 3,14 como aproximação para π.
Para atender à sua decisão, qual tipo de suporte a proprietária comprou?
Pelo enunciado, temos três recipientes, (de xampu, condicionador e sabonete líquido), sendo que cada produto tem a forma de um cilindro circular reto de raio igual a 3 cm. Então, precisamos identificar qual suporte comporta as bases dos recipientes.
Não é possível acondicionar os recipientes I, III e IV.
Então, vamos analisar os recipientes II e V.

Também, temos que analisar o suporte que tiver a base de menor área. Logo:
Para figura II (quadrado):
[tex] A = L^{2} = 12^{2} = 144\ cm^{2}[tex]
Para figura V (um quarto de círculo):
[tex]A = \frac{1}{4} π R^{2} = \frac{1}{4} \cdot 3,14 \cdot 13^{2} [tex]
[tex]A = \frac{3,14}{4} \cdot 169 [tex]
[tex]A = 0,785 \cdot 169 [tex]
[tex] A = 132,66\ cm^{2} [tex]
Logo, a área da figura V é menor que a área da figura II.
Portanto, alternativa "E".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Um técnico gráfico constrói uma nova folha a partir das medidas de uma folha A0. As medidas de uma folha A0 são 595 mm de largura e 840 mm de comprimento. A nova folha foi construída do seguinte modo: acrescenta uma polegada na medida da largura e 16 polegadas na medida do comprimento. Esse técnico precisa saber a razão entre as medidas da largura e do comprimento, respectivamente, dessa nova folha.
Considere 2,5 cm como valor aproximado para uma polegada.
Qual é a razão entre as medidas da largura e do comprimento da nova folha?
A configuração da nova folha é:

Como 1 polegada = 2,5 cm = 25 mm. Logo:
Comprimento: 840 mm + (16 × 25) mm = 840 mm + 400 mm = 1 240 mm
Largura = 595 mm + (1 × 25) mm = 595 mm + 25 mm = 620 mm
Com isso, a razão é:
[tex] Razão = \frac{largura}{comprimento}[tex]
[tex] Razão = \frac{620}{1\ 240}[tex]
Portanto, alternativa "B".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Um ciclista faz um treino para uma prova, em um circuito oval, cujo percurso é de 800 m. Nesse treino, realiza 20 voltas. Ele divide seu treino em 3 etapas. Na primeira etapa, inicializa seu cronômetro e realiza as cinco primeiras voltas com velocidade média de 4 m/s. Na segunda etapa, faz mais cinco voltas, mas com velocidade média 25% maior que a da etapa anterior. Na última etapa, finaliza o treino mantendo a velocidade média da primeira etapa.
Ao final do treino, o cronômetro estará marcando, em segundo,
ΔS = 5 voltas × 800 m = 4 000 m
ΔT(1) = ?
Vm = 4 m/s
[tex] V_{m} = \frac{Δs}{Δt(1)} [tex]
[tex] Δt(1) = \frac{Δs}{V_{m}} [tex]
[tex] Δt(1) = \frac{4\ 000\ m}{4\ m/s} = 1\ 000\ s[tex]
ΔS = 5 voltas × 800 m = 4 000 m
ΔT(2) = ?
Vm = 4 m/s + 25% de 4 m/s = 4 × 1,25 = 5 m/s
[tex] V_{m} = \frac{Δs}{Δt(2)} [tex]
[tex] Δt(2) = \frac{Δs}{V_{m}} [tex]
[tex] Δt(2) = \frac{4\ 000\ m}{5\ m/s} = 800\ s[tex]
ΔS = 10 voltas × 800 m = 8 000 m
ΔT(3) = ?
Vm = 4 m/s
[tex] V_{m} = \frac{Δs}{Δt(3)} [tex]
[tex] Δt(3) = \frac{Δs}{V_{m}} [tex]
[tex] Δt(3) = \frac{8\ 000\ m}{4\ m/s} = 2\ 000\ s[tex]
Dessa forma, o tempo total gasto é de:
[tex]Δt = Δt(1) + Δt(2) + Δt(3) [tex]
[tex]Δt = 1\ 000 + 800 + 2\ 000 [tex]
[tex]Δt = 3\ 800\ s[tex]
Portanto, alternativa "D".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Os pneus estão entre os itens mais importantes para a segurança de um carro. Segundo revendedores especializados, o desgaste do pneu em um trajeto é diretamente proporcional ao número de voltas que ele efetua em contato com o solo, sem derrapar, durante esse trajeto, sendo que constante de proporcionalidade k depende do material empregado na sua fabricação. O proprietário de um carro, cujo diâmetro do pneu mede L m, conforme indicado na imagem, pretende obter uma expressão que forneça uma estimativa para a medida do desgaste D desse pneu ao longo de uma viagem de x km. Para efeito dos cálculos, considerou o diâmetro do pneu como sendo L, independentemente da extensão do trajeto.

O valor de D é dado pela expressão
Pelo enunciado, temos:
"Segundo revendedores especializados, o desgaste do pneu em um trajeto é diretamente proporcional ao número de voltas que ele efetua em contato com o solo, sem derrapar, durante esse trajeto, sendo que constante de proporcionalidade k depende do material empregado na sua fabricação."
[tex]D = k\ \cdot\ (número\ de\ voltas)[tex] (equação I)
"O proprietário de um carro, cujo diâmetro do pneu mede L m, conforme indicado na imagem, pretende obter uma expressão que forneça uma estimativa para a medida do desgaste D desse pneu ao longo de uma viagem de x km." Como o pneu tem L metros de diâmetro. Seu raio (R) vale a metade de L, ou seja, metros. Também, o comprimento da circunferência, cuja fórmula é [tex]C = 2πR[tex], será igual a:
[tex]C = 2π \cdot \frac{L}{2} = π\ \cdot\ L\ metros [tex]
Então, para sabermos o número de voltas, basta dividirmos a distância de x km, que é igual a [tex]x \cdot 1000\ metros[tex], pelo comprimento da circunferência [tex]x \cdot L\ metros[tex].
[tex] \frac{x\ \cdot\ 1000\ metros}{π\ \cdot\ L\ metros} = \frac{x\ \cdot\ 1000}{π\ \cdot\ L}\ voltas [tex]
Podemos concluir que o número de voltas desse pneu de L metros de diâmetro, num trajeto de x km, será de [tex] \frac{x\ \cdot\ 1000}{π\ \cdot\ L}\ voltas [tex].
Agora, basta substituirmos este valor na Equação (I):
[tex] D = k\ (número\ de\ voltas)[tex]
[tex] D = k\ \cdot\ \frac{x\ \cdot\ 1000}{π\ \cdot\ L}[tex]
[tex] D = \frac{1\ 000\ \cdot\ k\ \cdot\ x}{π\ \cdot\ L}[tex]
Portanto, alternativa "B".
(Créditos da resolução: https://www.exercicios-resolvidos.com.)
(ENEM 2021 - 2ª Aplicação).
Um agricultor utilizava toda a área de uma região plana, em formato retangular, com 50 m de largura e 240 m de comprimento, para o plantio de mudas. Seguindo recomendações técnicas, cada muda é plantada no centro de uma pequena região retangular de 10 cm de largura por 20 cm de comprimento.
Esse agricultor decidiu ampliar a área destinada ao plantio de mudas, utilizando agora um terreno, também plano, em formato retangular, com 100 m de comprimento por 200 m de largura. As mudas deverão ser plantadas respeitando-se as mesmas recomendações técnicas.
Com o aumento da área destinada ao plantio, a quantidade máxima de mudas que poderão ser plantadas a mais é
Observe que:
Área inicial: A1 = 50 m × 240 m = 5 000 cm × 24 000 cm
Nova área: A2 = 100 m × 200 m = 10 000 cm × 20 000 cm
Pelo enunciado, cada muda vai ocupar uma área de 10 cm x 20 cm.
Primeiro, encontrar a quantidade mudas na área inicial A1. Isso é obtido multiplicando a largura do terreno divido pela largura da muda) × (comprimento do terreno dividido pelo comprimento da muda.
[tex]Quant.\ de\ mudas = \frac{5\ 000}{10} \cdot \frac{24\ 000}{20} [tex]
[tex]Quant.\ de\ mudas = 500 \cdot 1\ 200 = 600\ 000 [tex]
Agora, encontrar a quantidade mudas na nova área: (A2):
[tex]Quant.\ de\ mudas = \frac{10\ 000}{10} \cdot \frac{20\ 000}{20} [tex]
[tex]Quant.\ de\ mudas = 1\ 000 \cdot 1\ 000 = 1\ 000\ 000 [tex]
Finalmente, com o aumento da área destinada ao plantio, a quantidade máxima de mudas que poderão ser plantadas a mais é:
[tex]= 1\ 000\ 000\ -\ 600\ 000 [tex]
[tex]= 400\ 000 [tex]
Portanto, alternativa "B".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Coloquei uma pizza no forno às 8 h, momento em que o cachorro saiu para o quintal. Após 15 minutos, o telefone tocou, atendi e fiquei 4 minutos conversando. Ah, lembrei que, 5 minutos antes de o telefone tocar, meu vizinho tocou a campainha, eu atendi e ele disse que iria pegar uma encomenda no correio. Eu pedi para que ele pegasse a minha também. Nossa conversa durou 3 minutos e, após 30 minutos, ele voltou com a minha encomenda. Eu abri a porta para atendê-lo, quando o cachorro aproveitou para entrar em casa. Nossa conversa durou apenas 2 minutos, mas a pizza não queimou, porque eu já tinha tirado do forno 15 minutos antes de me despedir do vizinho. Os quadrinhos, dispostos em ordem aleatória, representam momentos da situação descrita e formam a base do raciocínio usado para determinar o tempo que a pizza ficou no forno.

A ordem cronológica das ações relatadas no texto, relativas à medição do tempo transcorrido, é representada pela sequência de quadrinhos
1º Quadrinho - (5): Colocou a pizza no forno ás 8 h momento em que o cachorro saiu para o quintal.
2º Quadrinho – (4): Após 15 minutos, o telefone tocou, atendi e fiquei 4 minutos conversando.
3º Quadrinho – (3): Ah, lembrei que, 5 minutos antes de o telefone tocar, meu vizinho tocou a campainha, eu atendi e ele disse que iria pegar uma encomenda no correio. Nossa conversa durou 3 minutos e, após 30 minutos, ele voltou com a minha encomenda.
4º Quadrinho – (2): Nossa conversa durou apenas 2 minutos, mas a pizza não queimou, porque eu já tinha tirado do forno 15 minutos antes de me despedir do vizinho.
2º Quadrinho – (1): Eu abri a porta para atendê-lo, quando o cachorro aproveitou para entrar em casa.
Portanto, alternativa "E".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Uma empresa produz painéis solares de energia elétrica, com a forma de retângulo, que geram 5 MWh (megawatts-hora) por metro quadrado. Cada painel tem 3 m de largura e 6 m de comprimento. O selo verde de eficiência é obtido se cada painel solar gerar, no mínimo, 150 MWh de energia solar. Para obter o selo verde, a empresa decide alterar apenas a largura dos seus painéis solares.
O número mínimo, em metro, que a empresa deve aumentar na largura dos seus painéis solares é
Pelo enunciado é preciso que cada painel gere no mínimo 150 MWh de energia solar. E, que cada 1 m² são gerados 5 MWH.
Vamos primeiro encontrar a medida mínima para produzir 150 MWH.
[tex]1\ m^{2} ---- 5\ MWh [tex]
[tex]x\ m^{2} ---- 150\ MWh [tex]
[tex] 5x = 150 [tex]
[tex] x = \frac{150}{5} [tex]
[tex] x = 30\ m^{2} [tex]
Como as placas solares são retangulares e a empresa decida alterar somente a largura. Logo:
[tex] Área = Comprimento × largura [tex]
[tex] Área = 6 × (3 + y) [tex]
[tex] 30 = 6 × (3 + y) [tex]
[tex] \frac{30}{6} = 3 + y [tex]
[tex] 5 = 3 + y [tex]
[tex] 5 - 3 = y [tex]
[tex] y = 2\ m [tex]
Dessa forma, o número mínimo, em metro, que a empresa deve aumentar na largura dos seus painéis solares é 2 m.
Portanto, alternativa "A".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Utiliza-se o termo download para designar o processo pelo qual um arquivo é transferido de algum sítio da internet para o dispositivo do usuário (computador, tablet, celular). Quando a transferência é interrompida, diz-se que o download travou. O esboço do gráfico representa a evolução do download de um arquivo que demorou 16 segundos para ser concluído.

Por quanto tempo, em segundo, esse download ficou travado?
O download ficou travado de 3s a 6s e de 10s a 12s. Logo:
[tex]= (6 - 3) + (12 - 10) [tex]
[tex] = 3 + 2 = 5\ segundos [tex]
[tex] = 5\ segundos [tex]
Portanto, alternativa "B".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Descenso noturno fisiológico é definido como uma redução maior ou igual a 10% da medida da pressão arterial (PA) sistólica registrada entre o período de vigília e o período de sono. O exame para avaliar se um indivíduo apresenta ou não descenso fisiológico é chamado de MAPA e consiste no monitoramento da evolução da PA sistólica do indivíduo ao longo de 24 horas. O resultado desse exame consiste em um gráfico no qual a região correspondente ao período de sono está hachurada em azul.
Cinco pacientes foram submetidos a esse exame, e os resultados mostram que apenas um paciente apresentou ausência de descenso noturno.
MELO, R. O. V. et al. Ausência de descenso noturno se associa a acidente vascular cerebral e infarto do miocárdio. Arq. Bras. Cardiol., n. 94, 2010.
O gráfico que indica o resultado do exame do paciente que apresentou ausência de descenso noturno é
Pelo enunciado, o descenso noturno fisiológico é definido como uma redução maior ou igual a 10% da medida da pressão arterial (PA) sistólica registrada entre o período de vigília e o período de sono.
Vamos analisar os gráficos: (Vamos analisar a opção (E) que ocorreu a menor redução).
E) redução de uma linha: 150 mmHg ∙ 10 % = 15 mmHg. Então:
[tex]= 150\ – 15\ = 135\ mmHg [tex]
Então, a redução não foi menor que 10%.
Portanto, alternativa "E".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
No rótulo de uma lata com 350 mL de um refrigerante, é possível descobrir que o valor energético é de 85 kcal (quilocalorias) a cada 200 mL de refrigerante. Por recomendação de um nutricionista, um paciente que consumia em sua dieta 2 800 kcal por dia mudou o hábito de consumir o conteúdo de 2 latas desse refrigerante por dia para consumir 2 latas de suco, cujo rótulo indicava um valor energético de 25 kcal por lata.
Em relação à sua dieta original, o consumo energético diário do paciente diminuiu, em porcentagem, o valor mais próximo de
Em relação à sua dieta original, o consumo energético diário do paciente diminuiu, em porcentagem, o valor mais próximo de:
[tex] 2\ 800\ kcal\ ----\ 100 \%[tex]
[tex] 247,5\ kcal\ -----\ x \% [tex]
[tex]2\ 800x = 247,5\ \cdot\ 100 [tex]
[tex] x = \frac{247,5\ \cdot\ 1\color{Red}{00}}{2\ 8\color{Red}{00}} [tex]
[tex] x = \frac{247,5}{28} [tex]
[tex] x \cong\ 8,8 \% [tex]
A redução percentual foi de aproximadamente 8,8%.
Portanto, alternativa "D".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Uma operadora de telefonia oferece cinco planos de serviços. Em cada plano, para cada mês, o cliente paga um valor V que lhe dá direito a telefonar por M minutos para clientes da mesma operadora. Quando a duração total das chamadas para clientes da mesma operadora excede M minutos, é cobrada uma tarifa T1 por cada minuto excedente nesse tipo de chamada. Além disso, é cobrado um valor T2, por minuto, nas chamadas para clientes de outras operadoras, independentemente do fato de os M minutos terem ou não sido usados. A tabela apresenta o valor de V, M, T1 e T2 para cada um dos cinco planos.
| V (R$) | M min | T1 R$/min | T2 R$/min | |
|---|---|---|---|---|
| Plano A | 25,00 | 20 | 1,50 | 2,00 |
| Plano B | 60,00 | 65 | 1,00 | 1,20 |
| Plano C | 60,00 | 75 | 1,00 | 1,50 |
| Plano D | 120,00 | 160 | 0,80 | 0,90 |
| Plano E | 120,00 | 180 | 0,80 | 1,20 |
Se um cliente dessa operadora planeja telefonar durante 75 minutos para amigos da mesma operadora e 50 minutos para amigos de outras operadoras, o plano que ele deverá escolher, a fim de pagar menos, é o
Vamos calcular o custo dos diferentes planos para identificar o preço mais em conta, sabendo que o cliente deseja telefonar por 75 minutos para amigos da mesma operadora e 50 minutos para amigos de outras operadoras. Logo:
A = 25 + (75 – 20) ∙ 1,50 + 50 ∙ 2 = R$ 207,50
B = 60 + (75 – 65) ∙ 1,00 + 50 ∙ 1,20 = R$ 130,00
C = 60 + 0 ∙ 1,00 + 50 ∙ 1,50 = R$ 135,00
D = 120 + 0 ∙ 0,80 + 50 ∙ 0,90 = R$ 165,00
E = 120 + 0 ∙ 0,80 + 50 ∙ 1,20 = R$ 180,00
Portanto, alternativa "B".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Um cinema tem capacidade para 180 pessoas e cobra R$ 30,00 pelo ingresso inteiro e R$ 15,00 pelo ingresso de meia-entrada. A ocupação média é de 100 pessoas e, destas, 60 pagam meia-entrada e as demais, o valor inteiro. O administrador desse cinema realizou algumas pesquisas com os seus frequentadores e constatou que, para cada R$ 2,00 de desconto no preço inteiro e R$ 1,00 de desconto no preço da meia-entrada, a quantidade de frequentadores pagantes do preço inteiro aumentava em 20% e a de pagantes de meia-entrada aumentava em 10% em relação às quantidades iniciais.
A hipótese do administrador do cinema é que esse comportamento se mantenha para novos descontos, ou seja, ao duplicar o valor dos descontos, duplicarão também os percentuais de aumento do número de frequentadores de cada tipo. Por isso, ele decidiu criar uma promoção aplicando um desconto de R$ 8,00 no preço inteiro e de R$ 4,00 no preço da meia-entrada, visando aumentar a arrecadação.
Ele classificará o sucesso da promoção em função do aumento na arrecadação da seguinte forma:
• fraco: aumento até R$ 500,00;
• regular: aumento maior que R$ 500,00 até R$ 800,00;
• bom: aumento maior que R$ 800,00 até R$ 1 200,00;
• muito bom: aumento maior que R$ 1 200,00 até R$ 2 000,00;
• ótimo: aumento maior que R$ 2 000,00.
Caso a hipótese do administrador do cinema seja confirmada, o sucesso da promoção será classificado como
A arrecadação inicial é igual a 40 pessoas pagando 30 reais mais 60 pessoas pagando 15 reais é de:
Arrecadação inicial = 40 ∙ 30 + 60 ∙ 15 = R$ 2 100,00
Agora, o administrador vai dar 8 reais de desconto no preço inteiro. É informado que para cada 2 reais de desconto no preço inteiro, aumenta-se em 20% a quantidade de clientes de preço inteiro. Como ele está dando 8 reais de desconto, que é (4 ∙ 2), então o aumento de clientes de preço inteiro será de (4 ∙ 20%) = 80%.
Clientes de preço inteiro = 40 + (80% de 40)
Clientes de preço inteiro = 40 + (0,8 ∙ 40)
Clientes de preço inteiro = 40 + 32
Clientes de preço inteiro = R$ 72,00
Além disso, o administrador vai dar 4 reais de desconto na meia entrada. Ou seja, para cada 1 real de desconto no preço de meia-entrada, aumenta-se em 10% a quantidade de clientes de meia-entrada. Como ele está dando 4 reais de desconto, que é (4 ∙ 1), então o aumento de clientes de meia-entrada será de (4 x 10%) = 40%.
Clientes de preço meia-entrada = 60 + (40% de 60)
Clientes de preço inteiro = 60 + (0,4 ∙ 60)
Clientes de preço inteiro = 60 + 24
Clientes de preço inteiro = R$ 84,00
Observe que (72 + 84) < 180 que é a capacidade máxima do cinema.
Como os descontos só estão atraindo (72 + 84) = 156 clientes.
Nova Arrecadação = 72 ∙ (30 – 8) + 84 ∙ (15 – 4)
Nova Arrecadação = 72 ∙ 22 + 84 ∙ 11
Nova Arrecadação = 1 584 + 924
Nova Arrecadação = R$ 2 508,00
Finalmente, podemos visualizar que a arrecadação subiu de 2100 para 2508, ou seja, teve um aumento de:
2508 – 2100 = R$ 408,00
Este é um aumento classificado como "fraco: aumento até R$ 500,00".
Portanto, alternativa "A".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
A escala de temperatura Delisle (°D), inventada no século XVIII pelo astrônomo francês Joseph-Nicholas Delisle, a partir da construção de um termômetro, foi utilizada na Rússia no século XIX. A relação entre as temperaturas na escala Celsius (°C) e na escala Delisle está representada no gráfico pela reta que passa pelos pontos A e B.
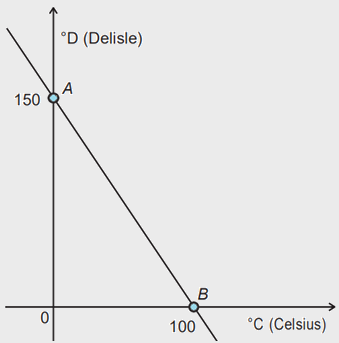
Disponível em: www.profibus.com.br. Acesso em: 22 mar. 2013.
Qual é a relação algébrica entre as temperaturas nessas duas escalas?
A relação algébrica pode encontrada através da equação da reta. A reta passa pelos pontos (0, 150 e (100, 0). Ou seja, [tex]y = mx + n [tex], sendo [tex] m[tex] o coeficiente angular e [tex]n[tex], o linear.
Calculo do coeficiente angular:
[tex]m = \frac{ΔC}{ΔD} = \frac{150\ -\ 0}{0\ -\ 100} = \frac{150}{-\ 100} = -\ 1,5[tex]
Observe:
[tex] D = -\ 1,5 + 150[tex] (× 2)
O coeficiente linear é o valor que a reta intercepta o eixo D. Ou seja, [tex]n = 150[tex]
[tex] 2D = -\ 3 + 300[tex]
[tex] 2D + 3C = 300[tex]
Portanto, alternativa "D".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Uma fórmula para calcular o Índice de Massa Corporal (IMC) foi publicada pelo Departamento de Nutrição da Universidade de São Paulo. O estudo propõe uma equação capaz de identificar os falsos magros que, apesar de exibirem uma silhueta esguia, apresentam altos níveis de gordura, e os falsos gordos, que têm um IMC alto em decorrência de ganho de massa muscular, e não de gordura. A equação considera a massa do indivíduo, além do peso e da estatura. A fórmula é expressa pela soma do triplo da massa (M), em quilograma, com o quádruplo do percentual de gordura (G), tudo dividido pela altura (H), em centímetro.
Disponível em: http://drauziovarella.com.br. Acesso em: 27 nov. 2012 (adaptado).
A expressão algébrica que representa a nova maneira de calcular o IMC é dada por
A fórmula é expressa pela soma do triplo da massa (M), em quilograma, com o quádruplo do percentual de gordura (G), tudo dividido pela altura (H), em centímetro.
[tex] \frac{3M\ +\ 4G}{H}[tex]
Portanto, alternativa "B".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Um diretor esportivo organiza um campeonato no qual haverá disputa de times em turno e returno, isto é, cada time jogará duas vezes com todos os outros, totalizando 380 partidas a serem disputadas.
A quantidade de times (x) que faz parte desse campeonato pode ser calculada pela equação
Quantidade de times: [tex]x[tex]
Quantidade de partidas que cada time joga em um turno: [tex]x - 1[tex]
Quantidade de jogos em dois turnos: [tex]2 (x - 1)[tex]
Agora, temos que multiplicar a quantidade de times (x) pelo valor encontrado acima e o resultado será: [tex]2x (x - 1)[tex]
Também, dividir por 2.
[tex]\frac{\color{Red}{2}x\ \cdot\ (x\ -\ 1)}{\color{Red}{2}} = 380[tex]
[tex]x(x - 1) = 380[tex]
[tex]x^{2} - 1 = 380[tex]
Portanto, alternativa "B".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Os preços médios da gasolina, etanol e diesel sofreram variações que foram registradas pela Agência Nacional de Petróleo, Gás Natural e Biocombustíveis (ANP), para a gasolina, em seis datas compreendidas no período entre 15 de outubro de 2015 e 13 de janeiro de 2016, conforme o gráfico.
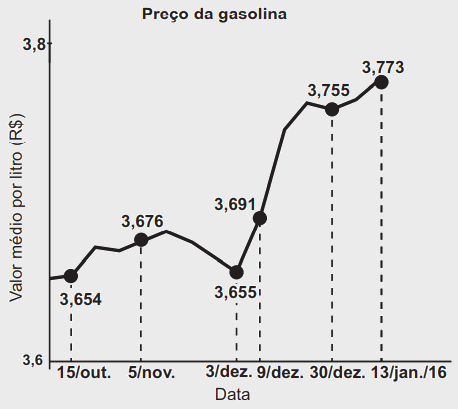
Disponível em: www.sistemasaltograndense.com. Acesso em: 30 nov. 2017 (adaptado).
Considerando-se os intervalos do período com valores informados no gráfico, o maior aumento, em valor absoluto do preço da gasolina, ocorreu no intervalo de
O maior aumento, em valor absoluto do preço da gasolina, ocorreu no intervalo de 9/dez. a 30/dez. Ou seja, subiu de 3,691 para 3,755. Logo:
= 3,755 – 3,691
= 0,64
Portanto, alternativa "D".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
O rendimento de um carro bicombustível (abastecido com álcool ou gasolina), popularmente conhecido como carro flex, quando abastecido com álcool é menor do que quando abastecido com gasolina, conforme o gráfico, que apresenta o rendimento médio dos carros populares.

Suponha que um cidadão fez uma viagem, cujo percurso foi de 1 009 km, em um carro popular flex, tendo abastecido o carro nos primeiros 559 km com gasolina e, no restante do percurso, com álcool. Considere que no momento do abastecimento não havia mais combustível no tanque.
Qual o valor mais próximo do rendimento médio do carro ao concluir todo o percurso de 1 009 km?
Pelo gráfico, encontramos que o rendimento do carro com gasolina é de 13 km/L e de 9 km/L com álcool. E, que o motorista percorreu 1009 km, sendo 559 km com gasolina e os outros (1009 – 559) = 450 km com álcool.
Agora, encontrar a quantidade de litros de gasolina ele gastou no primeiro trecho é:
[tex]\frac{559}{130} = 43\ litros\ de\ gasolina [tex]
A quantidade de litros de álcool ele gastou no segundo trecho é:
[tex]\frac{450}{9} = 50\ litros\ de\ álcool [tex]
O carro consumiu no total:
[tex]= 43 + 50 = 93\ litros\ de\ combustível [tex]
Agora, encontrar o rendimento médio do carro no percurso total:
[tex]\frac{1\ 009}{93} \cong\ 10,84\ km/h [tex]
Portanto, alternativa "C".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Considere que o modelo matemático utilizado no estudo da velocidade V, de uma partícula de um fluido escoando em um tubo, seja diretamente proporcional à diferença dos quadrados do raio R da secção transversal do tubo e da distância x da partícula ao centro da secção que a contém. Isto é, [tex]V(x) = K^{2}(R^{2} - x^{2})[tex], em que K é uma constante positiva.
O valor de x, em função de R, para que a velocidade de escoamento de uma partícula seja máxima é de
Desenvolvendo a expressão:
[tex]V(x) = K^{2}(R^{2} - x^{2})[tex]
[tex]V(x) = K^{2}R^{2} - K^{2}x^{2}[tex]
Observe que V(x) é uma equação do 2º grau. Então, os coeficientes são:
[tex]a = - K^{2}[tex], [tex]b = 0[tex] e [tex]c = K^{2}R^{2}[tex]
A parábola dessa função é voltada para baixo, pois [tex]a < 0[tex]. Então ela tem ponto de máximo. O valor de [tex]x[tex] é dado pelo [tex]Xv[tex] (X do vértice) é dado por:
[tex]x_{v} = \frac{-b}{2a} = \frac{0}{2(-K^{2})} = 0[tex]
Portanto, alternativa "A".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
A massa de um tanque de combustível depende:
I. da quantidade de combustível nesse tanque;
II. do tipo de combustível que se utiliza no momento;
III. da massa do tanque quando está vazio.
Sabe-se que um tanque tem massa igual a 33 kg quando está cheio de gasolina, 37 kg quando está cheio de etanol e que a densidade da gasolina é sete oitavos da densidade do etanol.
Qual é a massa, em quilograma, do tanque vazio?
Dados:
[tex]T[tex] = tanque de combustível
[tex]M_{G}[tex] = massa da gasolina
[tex]M_{E}[tex] = massa do etanol
[tex]D_{G}[tex] = Densidade da gasolina
[tex]D_{E}[tex] = Densidade do etanol
[tex] Densidade = \frac{massa}{volume}[tex]
Equacionando o problema:
[tex] \begin{cases} T + M_{G} = 33 \\ T + M_{E} = 37 \end{cases} (I) [tex]
Mas sabendo que a densidade da gasolina é sete oitavos da densidade do etanol. Logo:
[tex]D_{G} = \frac{7}{8} D_{E}[tex]
[tex]\frac{M_{G}}{\color{Red}{V_{G}}} = \frac{7}{8} \cdot \frac{M_{E}}{\color{Red}{V_{E}}}[tex], como [tex]V_{G} = V_{E}[tex]
[tex]M_{G} = \frac{7}{8} \cdot M_{E}[tex] (II)
Agora, substituir (II) em (I).
[tex] \begin{cases} T + M_{G} = 33 \\ T + M_{E} = 37 \end{cases} [tex]
[tex] \begin{cases} T + \frac{7}{8} \cdot M_{E} = 33 × (-8)\\ T + M_{E} = 37 × (7)\end{cases} [tex]
[tex]+ \underline{ \begin{cases} -8T -\ 7 M_{E} = -264 \\ 7T + 7M_{E} = 259 \end{cases}} [tex]
[tex]- T = - 5 ×(-1)[tex]
[tex]T = 5\ kg[tex]
Portanto, alternativa "D".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Para um evento que acontecerá no centro de uma cidade, há a opção de três estacionamentos, que cobram da seguinte maneira:
| Estaciona- -mento X | Estaciona- -mento Y | Estaciona- -mento X |
|---|---|---|
| R$ 4,00 pela 1ª hora ou fração de hora | R$ 3,70 por hora ou fração de hora | R$ 5,00 pela 1ª hora ou fração de hora |
| R$ 2,50 por cada hora subsequente ou fração de hora | R$ 2,00 por cada hora subsequente ou fração de hora |
Duas pessoas que participarão do evento precisam estacionar seus carros, uma delas pelo período de 1 hora e 50 minutos e a outra pelo período de 4 horas, pretendendo cada uma pagar o menor preço total pelo uso do estacionamento.
Essas pessoas deverão optar, respectivamente, pelos estacionamentos
Primeira pessoa: período de 1 hora e 50 minutos.
Estacionamento X = 4,00 + 2,50 = R$ 6,50
Estacionamento Y = 3,70 + 3,70 = R$ 7,40
Estacionamento Z = 5,00 + 2,00 = R$ 7,00
Segunda pessoa: período de 4 horas.
Estacionamento X = 4,00 + 2,50 + 2,50 + 2,50 = R$ 11,50
Estacionamento Y = 3,70 + 3,70 + 3,70 + 3,70 = R$ 14,80
Estacionamento Z = 5,00 + 2,00 + 2,00 + 2,00 = R$ 11,00
Então, o menor preço são os estacionamentos X e Z, respectivamente.
Portanto, alternativa "A".
(Créditos da resolução: Curso Objetivo)
(ENEM 2021 - 2ª Aplicação).
Um casal decidiu aplicar em um fundo de investimentos que tem uma taxa de rendimento de 0,8% ao mês, num regime de capitalização composta.
O valor final F a ser resgatado, depois de n meses, a uma taxa de rendimento mensal x, é dado pela expressão algébrica [tex]F = C \cdot (1 + x)^{n}[tex], em que C representa o capital inicial aplicado.
O casal planeja manter a aplicação pelo tempo necessário para que o capital inicial de R$ 100.000,00 duplique, sem outros depósitos ou retiradas.
Fazendo uso da tabela, o casal pode determinar esse número de meses.
| Y | Log Y |
|---|---|
| 1,008 | 0,003 |
| 1,08 | 0,03 |
| 1,8 | 0,20 |
| 2 | 0,30 |
| 3 | 0,47 |
Para atender ao seu planejamento, o número de meses determinado pelo casal é
Pretende encontrar o tempo para dobrar o capital. Logo:
[tex]F = C \cdot (1 + x)^{n}[tex]
[tex]200\ 000 = 100\ 000 \cdot (1 + 0,8 \%)^{n}[tex]
[tex]\frac{200\ 000}{100\ 000 } = (1 + 0,008)^{n}[tex]
[tex]2 = (1,008)^{n}[tex]
Agora, aplicar logaritmos de ambos os lados:
[tex]2 = (1,008)^{n}[tex]
[tex]log (2) = log(1,008)^{n}[tex]
[tex]log (2) = n \cdot log(1,008)[tex]
[tex]\frac{log 2}{log(1,008)} = n [tex]
[tex] n = \frac{0,30}{0,003} [tex]
[tex] n = 100\ meses [tex]
Portanto, alternativa "C".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Uma confeiteira pretende divulgar em um sítio da internet os doces que produz, mas só fará isso se acreditar que o número de acessos por semana compensará seu gasto com a divulgação. Por isso, pediu que lhe enviassem dados sobre o número de acessos ao sítio nas últimas 5 semanas e recebeu o gráfico a seguir.

A confeiteira acredita que, se o número de acessos mantiver o mesmo crescimento semanal para as próximas 5 semanas, ao final desse período valerá a pena investir na divulgação.
O número de acessos que a confeiteira acredita ser suficiente para que a divulgação no sítio valha a pena é
Observa-se que está aumentando 2 acessos por semana. Então, nas próximas 5 semanas, mantendo o mesmo ritmo de crescimento semanal, teremos:
152 – 154 – 156 – 157 – 160 – 162 – 164 – 166 – 168 – 170
Portanto, alternativa "B".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
O gráfico informa a produção registrada por uma indústria nos meses de janeiro, março e abril.
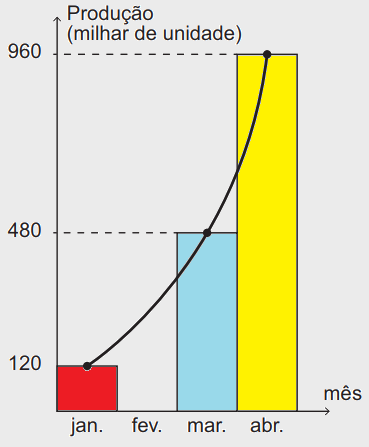
Por problemas logísticos, não foi feito o levantamento sobre a produção no mês de fevereiro. Entretanto, as informações dos outros três meses sugerem que a produção nesse quadrimestre cresceu exponencialmente, conforme aponta a curva de tendência traçada no gráfico.
Assumindo a premissa de que o crescimento nesse período foi exponencial, pode-se inferir que a produção dessa indústria no mês de fevereiro, em milhar de unidade, foi
É uma questão que explora função exponencial e progressão geométrica. No gráfico, mensalmente a produção dobra de tamanho. Podemos visualizar que a produção está formando uma Progressão geométrica (PG) de razão de 2.
(120, [tex]x[tex], 480, 960)
Podemos visualizar que o [tex]x[tex] tem que valer 240, uma vez que:
120 × 2 = 240
240 × 2 = 480
480 × 2 = 960.
Portanto, alternativa "C".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
O preço médio cobrado por um pintor para executar um serviço consiste em uma taxa fixa de R$ 25,00 mais uma quantia proporcional à área pintada. O quadro apresenta os valores cobrados por ele em trabalhos recentes.
| Área pintada (m²) | Total a pagar (R$) |
|---|---|
| 5 | 35,00 |
| 10 | 45,00 |
| 20 | 65,00 |
| 40 | 105,00 |
| 80 | 185,00 |
Qual o preço cobrado para realizar um serviço de pintura de uma área de 150 m²?
Analisando a tabela para a área de 5 e 10 m² percebe-se que existe um valor fixo. Então:
45 – 35 = R$ 10,00. Então, o valor fixo é: R$ 25,00
Agora, também podemos encontrar o valor por m².
[tex] \frac{R \$\ 10,00}{5\ m^{2}} = R \$\ 2,00\ por\ m^{2}[tex]
Então, podemos obter uma função:
[tex]P(x) = 25 + 2x [tex]
Dessa forma, podemos encontrar agora o valor para 150 m².
[tex]P(x) = 25 + 2x [tex]
[tex]P(150) = 25 + 2 \cdot 150 [tex]
[tex]P(150) = 25 + 300 [tex]
[tex]P(150) = R \$\ 325,00 [tex]
Portanto, alternativa "B".
(Créditos da resolução: Curso Objetivo)
(ENEM 2021 - 2ª Aplicação).
O crescimento de uma população de microrganismos é descrito pela expressão [tex] K(t) = 81 \cdot 3^{\frac{1}{3}t} + 2[tex], em que [tex]K(t)[tex] indica a quantidade de microrganismos em um meio de cultura em função do tempo [tex]t[tex]. O gráfico representa a evolução de [tex]K[tex] em relação ao tempo [tex]t[tex].

Com base nos dados, o valor de [tex]m[tex] é
O valor de [tex]m[tex] é:
[tex] K(t) = 81 \cdot 3^{\frac{1}{3}t} + 2[tex]
[tex]6\ 563 = 81 \cdot 3^{\frac{1}{3}m} + 2[tex]
[tex]6\ 563\ -\ 2 = 81 \cdot 3^{\frac{1}{3}m}[tex]
[tex]6\ 561 = 81 \cdot 3^{\frac{1}{3}m}[tex]
[tex]\frac{6\ 561}{81} = 3^{\frac{1}{3}m}[tex]
[tex]81 = 3^{\frac{1}{3}m}[tex]
[tex]3^{4} = 3^{\frac{1}{3}m}[tex]
Agora, igualando os expoentes:
[tex]4 = \frac{1}{3}m[tex]
[tex]1m = 4 \cdot 3[tex]
[tex]m = 12[tex]
Portanto, alternativa "D".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Um laboratório farmacêutico pretende implementar a entrega própria de seus produtos em uma cidade, dentre as cinco cidades onde hoje esse serviço é terceirizado. Obteve relatórios dos seus entregadores terceirizados destacando: a quantidade (em litro) de combustível gasto em cada dia de entrega, o valor do combustível na respectiva cidade da entrega e os gastos com a limpeza diária do veículo após as entregas realizadas. Os valores desses itens, em real, estão apresentados no quadro.
| Litros de combústivel gastos por dia | Preço da limpeza do carro | Preço por litro do combústivel | |
|---|---|---|---|
| SP | 7,5 | 20,00 | 2,50 |
| CWB | 9,5 | 15,50 | 2,40 |
| BH | 8,0 | 16,50 | 2,24 |
| RJ | 14,5 | 18,00 | 2,10 |
| BSB | 13,0 | 15,00 | 3,00 |
A diretoria desse laboratório implementará a entrega própria na cidade que apresentar o menor gasto diário desse serviço.
Em qual cidade a implementação do serviço de entrega própria será realizada?
Calcular o gasto diário para cada cidade:
São Paulo: 7,5 ∙ 2,50 + 20,00 = 18,75 + 20,00 = R$ 38,75
Curitiba: 9,5 ∙ 2,40 + 15,50 = 22,56 + 15,50 = R$ 38,06
Belo Horizonte: 8,0 ∙ 2,24 + 16,50 = 17,92 + 16,50 = R$ 34,42
Rio de Janeiro: 14,5 ∙ 2,10 + 18,00 = 29,60 + 18,00 = R$ 47,61
Brasília: 13 ∙ 3,00 + 15,00 = 39,00 + 15,00 = R$ 54,00
Dessa forma, a cidade de Belo Horizonte tem o serviço de entrega mais barato.
Portanto, alternativa "A".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Um nutricionista preparou cinco opções de dieta para seus clientes. A quantidade de calorias, em quilocaloria, de cada dieta é apresentada no quadro, em função de três componentes básicos: proteínas, carboidratos e suplementos.
| Dieta | I | II | III | IV | V |
|---|---|---|---|---|---|
| Proteínas (kcal) | 66 | 57 | 63 | 66 | 69 |
| Carboidratos (kcal) | 42 | 42 | 39 | 48 | 36 |
| Suplementos (kcal) | 87 | 105 | 96 | 84 | 93 |
Como um de seus clientes apresentou muita redução de massa corporal, o nutricionista recomendou que ele escolhesse uma das cinco dietas do quadro e quadruplicasse a quantidade de proteínas, triplicasse a quantidade de carboidratos e duplicasse a quantidade de suplementos recomendadas pela dieta escolhida.
O cliente seguirá a recomendação do nutricionista, mas deseja escolher a dieta na qual ele consumirá a menor quantidade de calorias dentre as opções disponíveis.
O cliente deverá escolher a dieta
Observe a quantidade de calorias de cada cliente:
Cliente I: 66 ∙ 4 + 42 ∙ 3 + 87 ∙ 2 = 264 + 126 + 174 = 564 kcal
Cliente II: 57 ∙ 4 + 42 ∙ 3 + 105 ∙ 2 = 228 + 126 + 210 = 564 kcal
Cliente III: 63 ∙ 4 + 39 ∙ 3 + 96 ∙ 2 = 252 + 117 + 288 = 657 kcal
Cliente IV: 66 ∙ 4 + 48 ∙ 3 + 84 ∙ 2 = 264 + 144 + 168 = 576 kcal
Cliente V: 69 ∙ 4 + 36 ∙ 3 + 93 ∙ 2 = 276 + 108 + 186 = 570 kcal
Portanto, alternativa "C".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Até a Copa de 2010, apenas sete jogadores haviam conseguido o feito de marcar 8 ou mais gols em uma mesma edição da Copa do Mundo. O quadro apresenta os anos das edições da copa nas quais ocorreram esses feitos, quais foram os jogadores que os realizaram e os respectivos números de gols marcados por cada um deles.
| Ano | Nome do jogador | Número de gols marcados |
|---|---|---|
| 1930 | Quillermo Stábile | 8 |
| 1950 | Admir de Menezes | 9 |
| 1954 | Sandor Kocsis | 11 |
| 1958 | Just Fontaine | 13 |
| 1966 | Eusébio | 9 |
| 1970 | Gerd Muller | 10 |
| 2002 | Ronaldo Nazário | 8 |
Para facilitar a análise sobre a quantidade de gols marcados por esses artilheiros nas referidas copas, foi calculada a mediana da distribuição dos números de gols marcados por eles nas sete copas especificadas no quadro.
A mediana dessa distribuição é igual a
Ordenar em ordem crescente:
8 8 9 9 10 11 13
A mediana é o elemento central, ou seja, o número 9.
Portanto, alternativa "A".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
A qualidade de sementes é verificada, entre outros fatores, pelo índice de germinação. Uma grande empresa afirma que o índice de germinação de suas sementes é de 90%. Essa empresa e dez pequenos produtores que formam uma cooperativa estão concorrendo a um auxílio financeiro que permitirá aumentar os negócios. Os cooperados querem preparar um documento técnico comparando a qualidade de suas sementes com as da empresa. Eles discutiram a possibilidade de colocar nesse documento frases como:
I – A média de germinação de nossas sementes é superior ao índice de germinação anunciado pela empresa.
II – A mediana de germinação de nossas sementes é superior ao índice de germinação anunciado pela empresa.
III – A média de germinação de nossas sementes é igual ao índice de germinação anunciado pela empresa.
IV – A moda de germinação de nossas sementes é igual ao índice de germinação anunciado pela empresa.
V – A mediana de germinação de nossas sementes é igual ao índice de germinação anunciado pela empresa.
Eles decidiram anotar a porcentagem de germinação das sementes de cada cooperado, analisar as frases e decidir qual era a correta para, então, colocá-la no documento.
As porcentagens anotadas foram 90%, 65%, 70%, 75%, 95%, 95%, 90%, 80%, 80% e 90%.
A frase a ser colocada no documento é a de número
É uma questão que envolve média, moda e mediana.
Moda: variável que mais repeti: 90% (repetiu 3 vezes)
Mediana: Ordenar: 65%, 70%, 75%, 80%, 80%, 90%, 90%, 90%, 95%, 95%
[tex] Me = \frac{80 \%\ +\ 90 \% }{2} = \frac{170 \%}{2} = 85 \% [tex]
Média:
[tex] M = \frac{65 + 70 + 75 + 80 + 80 + 90 + 90 + 90 + 95 + 95}{10}[tex]
[tex] M = \frac{830}{10} = 83 \%[tex]
No ato de encontrar a moda já suficiente para responder a questão. Logo, “IV - A moda de germinação de nossas sementes (que vale 90%) é igual ao índice de germinação anunciado pela empresa (que foi anunciado como 90%)”.
Portanto, alternativa "D".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Em uma fábrica de circuitos elétricos, há diversas linhas de produção e montagem. De acordo com o controle de qualidade da fábrica, as peças produzidas devem seguir um padrão. Em um processo produtivo, nem todas as peças produzidas são totalmente aproveitáveis, ou seja, há um percentual de peças defeituosas que são descartadas. Em uma linha de produção dessa fábrica, trabalham três máquinas, M1 , M2 e M3 , dia e noite. A máquina M1 produz 25% das peças, a máquina M2 produz 30% e a máquina M3 produz 45%. O percentual de peças defeituosas da máquina M1 é de 2%, da máquina M2 é de 3% e da máquina M3 é igual a 4%.
A probabilidade de uma peça defeituosa ter sido produzida pela máquina M2 é mais próxima de
Dados:
E = quantidade de peças defeituosas produzidas por M2
E = 3% × 30%
U = total de peças defeituosas, ou seja, todas aquelas produzidas por M1, M2 e M3 juntas
U = 2% × 25% + 3% × 30% + 4% × 45%
Finalmente, temos que
[tex] P = \frac{E}{U}[tex]
[tex] P = \frac{3 \%\ ×\ 30\ \%}{2\ \%\ ×\ 25\ \%\ +\ 3\ \%\ ×\ 30\ \%\ +\ 4\ \%\ ×\ 45\ \%}[tex]
Pode-se eliminar %, pois está presente em todos os termos:
[tex] P = \frac{90}{50\ +\ 90\ +\ 180}[tex]
[tex] P = \frac{90}{320} = \frac{9}{32} \cong\ 0,281 \cong 28,1[tex]
Portanto, alternativa "B".
(Créditos da resolução: www.exercicios-resolvidos.com.)
(ENEM 2021 - 2ª Aplicação).
A senha de um cofre é uma sequência formada por oito dígitos, que são algarismos escolhidos de 0 a 9. Ao inseri-la, o usuário se esqueceu dos dois últimos dígitos que formam essa senha, lembrando somente que esses dígitos são distintos.
Digitando ao acaso os dois dígitos esquecidos, a probabilidade de que o usuário acerte a senha na primeira tentativa é
Primeiro encontrar o total de possibilidades de acertar os dois últimos dígitos da senha:
X X X X X X ? ?
↓ ↓
10 ∙ 9 = 90
Portanto, a probabilidade de que o usuário acerte a senha na primeira tentativa é:
Portanto, alternativa "B".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
O presidente de um time de futebol contratou, para a temporada de 2016, um atacante e um meio-campista. Para isso, ele recebeu do departamento de futebol dois quadros. O primeiro quadro contém o número de gols marcados por três candidatos a atacantes, nas três temporadas anteriores.
| Atacantes | 2013 (número de gols) | 2014 (número de gols) | 2015 (número de gols) |
|---|---|---|---|
| I | 13 | 13 | 24 |
| II | 13 | 16 | 22 |
| III | 17 | 11 | 20 |
O segundo quadro contém o número de assistências que resultaram em gol, feitas por dois candidatos a meios-campistas, nas três temporadas anteriores.
| Meios-campista | IV | V |
|---|---|---|
| 2013 (número de assistências) | 11 | 7 |
| 2014 (número de assistências) | 17 | 16 |
| 2015 (número de assistências) | 20 | 23 |
Após fazer uma análise das médias de gols de cada atacante e das médias de assistências de cada meio-campista nas últimas três temporadas, o presidente contratou o atacante e o meio-campista com maior média de gols e assistências, respectivamente, nessas três temporadas.
O atacante e o meio-campista escolhidos por esse presidente foram, respectivamente,
Médias de gols:
[tex]M(I) = \frac{13\ +\ 13\ +\ 24}{3} = \frac{50}{3}\ \cong\ 16,67 [tex]
[tex]M(II) = \frac{13\ +\ 16\ +\ 22}{3} = \frac{51}{3}\ = 17 [tex]
[tex]M(III) = \frac{17\ +\ 11\ +\ 20}{3} = \frac{48}{3}\ = 16 [tex]
Logo, a maior média é a do atacante II.
Agora, as médias das assistências:
[tex]M(IV) = \frac{11\ +\ 17\ +\ 20}{3} = \frac{48}{3}\ = 16 [tex]
[tex]M(V) = \frac{7\ +\ 16\ +\ 23}{3} = \frac{46}{3}\ \cong 15,33 [tex]
O meio-campista IV possui a maior média.
Portanto, alternativa "C".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Cinco atletas que participarão de uma maratona treinam frequentemente. As distâncias percorridas por eles no último treino estão registradas, em quilômetro, no quadro.
| 42,8 | 41,6 | 41,8 | 43,4 | 43,4 |
|---|
Um sexto atleta, que também participará da maratona, pretende realizar um treino percorrendo uma distância igual à média das distâncias percorridas pelos cinco atletas no último treino por eles realizado.
A distância, em quilômetro, que esse sexto atleta deverá percorrer em seu treino é
Calcular a média dos cinco atletas:
[tex]M = \frac{42,8\ +\ 41,6\ +\ 41,8\ +\ 43,4\ +\ 43,4}{5} [tex]
[tex]M = \frac{213}{5} [tex]
[tex]M = 42,6\ km [tex]
Então, o sexto atleta deverá percorrer em seu treino 42,6 km.
Portanto, alternativa "C".
(Créditos da resolução: Prof. Warles.o)
(ENEM 2021 - 2ª Aplicação).
Black Friday é uma tradição norte-americana que consiste numa queda de preços de uma grande variedade de produtos disponíveis para venda na última sexta-feira do mês de novembro. No Brasil, em muitas lojas, essa prática se estende por todo esse mês. Para esse período, o gerente de uma loja de produtos eletrônicos que tem 5 vendedores estabelece uma meta de vendas de computadores para um total mínimo de 605 unidades. Ele considera que a média de vendas de computadores dos 5 vendedores juntos neste ano se manterá igual à dos últimos 5 anos, conforme apresentada no gráfico. Considere que a participação de cada vendedor na obtenção da meta seja igual.

Para que a meta da loja seja atingida, o gerente deverá estipular, para cada vendedor, um aumento na média de vendas de, no mínimo, quantas unidades?
O gerente estabelece uma meta de vendas de 605 unidades para 5 vendedores neste ano. Agora, calcular esta média.
[tex]M = \frac{525\ +\ 480\ +\ 430\ +\ 440\ +\ 400}{5} [tex]
[tex]M = \frac{2\ 275}{5} [tex]
[tex]M = 455 [tex]
Observe que o gerente quer vender 605 unidades, porém a média esperada é de 455. Deste modo, será necessário aumentar as vendas em:
605 – 455 = 150 unidades
Pelo enunciado, a participação dos 5 vendedores na obtenção dessa meta será igual. Logo:
[tex]M = \frac{150}{5} [tex]
[tex]M = 30\ unidades [tex]
Portanto, alternativa "E".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Um professor tem uma despesa mensal de 10% do seu salário com transporte e 30% com alimentação. No próximo mês, os valores desses gastos sofrerão aumentos de 10% e 20%, respectivamente, mas o seu salário não terá reajuste. Com esses aumentos, suas despesas com transporte e alimentação aumentarão em R$ 252,00.
O salário mensal desse professor é de
Vamos considerar de “S” o salário mensal, sabendo o salário do professor não sofreu reajustes. Então:
Transporte: 10% S = 0,1 S
Alimentação: 30% S = 0,3 S
Com isso, temos que o gasto com transporte e alimentação é de:
0,10 S + 0,30 S = 0,40 S
Também, foi informado que o transporte e alimentação sofrerão aumentos de 10% (100% + 10% = 110% = 1,1) e 20% (100% + 20% = 120% = 1,2), respectivamente.
Transporte: 0,1 S ∙ 1,1 = 0,11 S
Alimentação: 0,3 S ∙ 1,2 = 0,36 S
O total gasto vai ser de:
0,11 S + 0,36 S = 0,47 S
Com os aumentos, as despesas com transporte e alimentação serão de R$ 252,00. Logo:
[tex] 0,47S - 0,40S = 252[tex]
[tex] 0,07\ S = 252[tex]
[tex]S = \frac{252}{0,07}[tex]
[tex]S = R \$\ 3\ 600,00[tex]
Portanto, alternativa "d".
(Créditos da resolução: Prof. Warles.)
(ENEM 2021 - 2ª Aplicação).
Uma loja que vende tintas tem uma máquina que efetua misturas de variadas cores para obter diferentes tonalidades. Um cliente havia comprado 7 litros de tinta de uma tonalidade, proveniente da mistura das cores verde e branco, na proporção de 5 para 2, respectivamente. Tendo sido insuficiente a quantidade de tinta comprada, o cliente retorna à loja para comprar mais 3,5 litros da mesma mistura de tintas, com a mesma tonalidade que havia comprado anteriormente.
A quantidade de tinta verde, em litro, que o funcionário dessa loja deverá empregar na mistura com a tinta branca para conseguir a mesma tonalidade obtida na primeira compra é
Como a mistura das cores verde e branco é na proporção de 5 para 2, respectivamente. Logo:
[tex] \frac{Tinta\ verde}{Mistura} = \frac{5}{5\ +\ 2} = \frac{x}{3,5}[tex]
[tex] 7x = 5 \cdot 3,5[tex]
[tex] x = \frac{17,5}{7}[tex]
[tex] x = 2,5\ litros\ de\ tinta\ verde[tex]
Portanto, alternativa "E".
(Créditos da resolução: Prof. Warles.)
