(ENEM 2009 - Edição anulada).
Para o cálculo da inflação, utiliza-se, entre outros, o índice Nacional de Preços ao Consumidor Amplo (IPCA), que toma como base os gastos das famílias residentes nas áreas urbanas, com rendimentos mensais compreendidos entre um e quarenta salários mínimos. O gráfico a seguir mostra as variações do IPCA de quatro capitais brasileiras no mês de maio de 2008.

Disponível em: http://www.ibge.gov.br. Acesso em: 05 jul. 2008 (adaptado).
Com base no gráfico, qual item foi determinante para a inflação de maio de 2008.
Nas quatro capitais, como pode ser observado no gráfico, o item que teve uma maior variação do IPCA no mês de maio foi de alimentação e bebidas. Como a inflação diz respeito às maiores variações então, a resposta correta é: Letra A.
(ENEM 2009 - Edição anulada).
No calendário utilizado atualmente, os anos são numerados em uma escala sem o zero, isto é, não existe o ano zero. A era cristã se inicia no ano 1 depois de Cristo (d.C.) e designa-se o ano anterior a esse como ano 1 antes de Cristo (a.C.). Por essa razão, o primeiro século ou intervalo de 100 anos da era cristã terminou no dia 31 de dezembro do ano 100 d.C., quando haviam decorrido os primeiros 100 anos após o início da era. O século II começou no dia 1 de janeiro do ano 101 d.C., e assim sucessivamente.
Como não existe o ano zero, o intervalo entre os anos 50 a.C. e 50 d.C., por exemplo, é de 100 anos. Outra forma de representar anos é utilizando-se números inteiros, como fazem os astrônomos. Para eles, o ano 1 a.C.
corresponde ao ano 0, o ano 2 a.C. ao ano – 1, e assim sucessivamente. Os anos depois de Cristo são representados pelos números inteiros positivos, fazendo corresponder o número 1 ao ano 1 d.C.
Considerando o intervalo de 3 a.C. a 2 d.C., o quadro que relaciona as duas contagens descritas no texto é

No enunciado do problema diz que o ano 1 a.C. corresponde ao ano zero, o ano 2 a.C. ao ano -1, 3 a.C. ao ano -2 e, como os anos d.C. correspondem aos números inteiros positivos, conclui-se que o ano 2 d.C. corresponde ao ano 2 e o ano 3 d.C. ao ano 3.
(ENEM 2009 - Edição anulada).
Na cidade de João e Maria, haverá shows em uma boate.
Pensando em todos, a boate propôs pacotes para que os fregueses escolhessem o que seria melhor para si.
Pacote 1 : taxa de 40 reais por show.
Pacote 2 : taxa de 80 reais mais 10 reais por show.
Pacote 3 : taxa de 60 reais para 4 shows, e 15 reais por cada show a mais.
João assistirá a 7 shows e Maria, a 4. As melhores opções para João e Maria são, respectivamente, os pacotes
No problema tem-se que João assistirá a 7 shows.
Se utilizar o “pacote 1”: 7 shows × 40 reais, gastará 280 reais.
Se utilizar o “pacote 2”: Taxa fixa de 80 reais mais 7 shows × 10 reais, gastará 150 reais, ou seja:
80 + 10 × 7 = 80 + 70 = 150 reais.
Se utilizar o “pacote 3”: 60 reais por 4 shows mais 3 shows × 15 reais, gastará 105 reais, ou seja:
60 + 15 × 3 = 60 + 45 = 105 reais.
Logo, o pacote 3 é mais econômico.
Tem-se também que Maria assistirá a 4 shows.
Se utilizar o “pacote 1”: 4 shows × 40 reais, gastará 160 reais.
Se utilizar o “pacote 2”: Taxa fixa de 80 reais mais 4 shows × 10 reais, gastará 120 reais, ou seja:
80 + 10 × 4 = 80 + 40 = 120 reais.
Se utilizar o “pacote 3”: Gastará 60 reais.
Logo, o pacote 3 é mais econômico.
(ENEM 2009 - Edição anulada).
Um decorador utilizou um único tipo de transformação geométrica para compor pares de cerâmicas em uma parede. Uma das composições está representada pelas cerâmicas indicadas por I e II.

Utilizando a mesma transformação, qual é a figura que compõe par com a cerâmica indicada por III?

Da figura I para a figura II foi feita a simetria em relação ao eixo horizontal que passa pelo centro da figura.

Utilizando-se o mesmo tipo de simetria na figura III, obtemos a figura IV abaixo.

(ENEM 2009 - Edição anulada).
Cinco equipes A, B, C, D e E disputaram uma prova de gincana na qual as pontuações recebidas podiam ser 0, 1, 2 ou 3. A média das cinco equipes foi de 2 pontos.
As notas das equipes foram colocadas no gráfico a seguir, entretanto, esqueceram de representar as notas da equipe D e da equipe E.

Mesmo sem aparecer as notas das equipes D e E, pode-se concluir que os valores da moda e da mediana são, respectivamente,
Como são cinco equipes. Logo, independentemente da pontuação das equipes D e E, a moda será 2,0, pois é a variável que mais repete.
Para a média aritmética ser 2, devemos ter:
[tex] \frac{2+2+2+D+E}{5} = 2 [tex]
[tex] 6 + D + E = 10 [tex]
[tex] D + E = 4 [tex]
Logo, as possibilidades para as equipes D e E, são:
1 + 3 = 4;
2 + 2 = 4
e
3 + 1 = 4
Desta forma, a mediana poderá ser:
Para D = 2 e E = 2:
2 - 2 - 2 - 2 - 2 Mediana 2
Para D = 1 e E = 3:
1 - 2 - 2 - 2 - 3 Mediana 2
Para D = 3 e E = 1:
1 - 2 - 2 - 2 - 3 Mediana 2
(ENEM 2009 - Edição anulada).
Muitas vezes o objetivo de um remédio é aumentar a quantidade de uma ou mais substâncias já existentes no corpo do indivíduo para melhorar as defesas do organismo. Depois de alcançar o objetivo, essa quantidade deve voltar ao normal.
Se uma determinada pessoa ingere um medicamento para aumentar a concentração da substância A em seu organismo, a quantidade dessa substância no organismo da pessoa, em relação ao tempo, pode ser melhor representada pelo gráfico

O problema diz que o objetivo do remédio é “aumentar” a quantidade de uma substância existente no corpo do indivíduo e depois de alcançado o objetivo, “voltar ao normal”.
Analisando os gráficos, temos:
Nas alternativas (A) e (B) a quantidade da substância A não volta ao normal;
na alternativa (C), a quantidade da substância A é zero, logo não possui substância A;
na alternativa (E) diminui a quantidade de substância A;
e, na alternativa (D), possui uma quantidade de substância A, aumenta depois de um determinado tempo, atingindo uma quantidade máxima, retornando a quantidade inicial, sendo então a alternativa correta.
(ENEM 2009 - Edição anulada).
O xadrez é jogado por duas pessoas. Um jogador joga com as peças brancas, o outro, com as pretas. Neste jogo, vamos utilizar somente a Torre, uma das peças do xadrez. Ela pode mover-se para qualquer casa ao longo da coluna ou linha que ocupa, para frente ou para trás, conforme indicado na figura a seguir.

O jogo consiste em chegar a um determinado ponto sem passar por cima dos pontos pretos já indicados.

Respeitando-se o movimento da peça Torre e as suas regras de movimentação no jogo, qual é o menor número de movimentos possíveis e necessários para que a Torre chegue à casa C1?
A menor quantidade de movimentos ocorre quando a torre percorre, em cada movimento, as maiores distâncias possíveis. O esquema seguinte mostra um possível percurso com apenas quatro movimentos.
São eles, H8 → H3, H3 → D3, D3 → D1 e D1 → C1.

(ENEM 2009 - Edição anulada).
Paulo emprestou R$ 5.000,00 a um amigo, a uma taxa de juros simples de 3% ao mês. Considere x o número de meses do empréstimo e M(x) o montante a ser devolvido para Paulo no final de meses.
Nessas condições, a representação gráfica correta para M(x) é
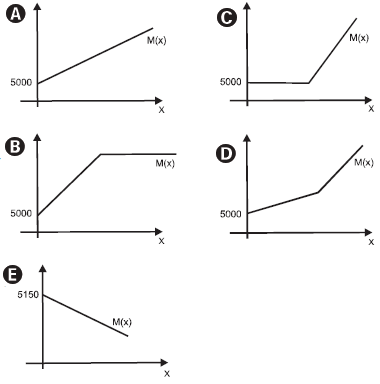
A função que relaciona o número x de meses com o montante M(x), a ser devolvido por Paulo é com x ∈ N, M(x) = 5000 e m(x) em reais. O gráfico correto seria

Dos gráficos apresentados optamos pelo da alternativa A.
(ENEM 2009 - Edição anulada).
Os calendários usados pelos diferentes povos da Terra são muito variados. O calendário islâmico, por exemplo, é lunar, e nele cada mês tem sincronia com a fase da lua. O calendário maia segue o ciclo de Vênus, com cerca de 584 dias, e cada 5 ciclos de Vênus corresponde a 8 anos de 365 dias da Terra.
MATSUURA. Oscar. Calendários e o fluxo do tempo Scientific American Brasil. Disponível em: http://www.uol.combr. Acesso em: 14 out. 2008 (adaptado).
Quantos ciclos teria, em Vênus, um período terrestre de 48 anos?
Veja que:
5 ciclos de Vênus ----- 8 anos terrestres
x ciclos de Vênus ----- 48 anos terrestres
[tex] x = \frac{5\ \cdot\ 48}{8} = 30\ ciclos [tex]
(ENEM 2009 - Edição anulada).
Considere que as médias finais dos alunos de um curso foram representadas no gráfico a seguir.

Sabendo que a média para aprovação nesse curso era maior ou igual a 6,0, qual foi a porcentagem de alunos aprovados?
Do gráfico temos:
4 alunos com nota 4,0; 10 alunos com nota 5,0; 18 alunos com nota 6,0; 16 aluno com nota 7,0 e 2 alunos com nota 8,0, num total de 4 + 10 + 18 + 16 + 2 = 50 alunos.
Desses, foram aprovados 18 + 16 + 2 = 36 alunos, correspondendo:
[tex] \frac{36}{50} = 0,72 = 72 \% [tex]
(ENEM 2009 - Edição anulada).
As abelhas domesticadas da América do Norte e da Europa estão desaparecendo, sem qualquer motivo. As abelhas desempenham papel fundamental na agricultura, pois são responsáveis pela polinização (a fecundação das plantas). Anualmente, apicultores americanos alugam 2 milhões de colmeias para polinização de lavouras. O sumiço das abelhas já inflacionou o preço de locação das colmeias. No ano passado, o aluguel de cada caixa (colmeia) com 50.000 abelhas estava na faixa de 75 dólares.
Depois do ocorrido, aumentou para 150 dólares. A previsão é que faltem abelhas para polinização neste ano nos EUA.
Somente as lavouras de amêndoa da Califórnia necessitam de 1,4 milhão de colmeias.
Disponível em: . Acesso em 23 fev 2009 (adaptado).
De acordo com essas informações, o valor a ser gasto pelos agricultores das lavouras de amêndoa da Califórnia com o aluguel das colmeias será de
1,4 milhões de colmeias a $ 150 cada geram aos agricultores das lavouras de amêndoas da Califórnia um gasto de:
1,4 milhões x U$ 150 = 210 milhões de dólares.
(ENEM 2009 - Edição anulada).
Em uma padaria, há dois tipos de forma de bolo, formas 1 e 2, como mostra a figura abaixo.

Sejam L o lado da base da forma quadrada, r o raio da base da forma redonda, A₁ e A₂ as áreas das bases das formas 1 e 2, e V₁ e V₂ os seus volumes, respectivamente.
Se as formas têm a mesma altura h, para que elas comportem a mesma quantidade de massa de bolo, qual é a relação entre r e L?
Os volumes [tex]V_{1}[tex] e [tex]V_{2}[tex] do bolo na forma de paralelepípedo e do bolo na forma de cilindro são tais que:
[tex] V_{1} = V_{2} [tex]
[tex] L^{2} \cdot h = π\ \cdot R^{2} \cdot h [tex]
[tex] L = \sqrt{π\ \cdot R^{2}} [tex]
[tex] L = r\sqrt{π} [tex]
(ENEM 2009 - Edição anulada).
Dados do Instituto de Pesquisas Econômicas Aplicadas (IPEA) revelaram que no biênio 2004/2005, nas rodovias federais, os atropelamentos com morte ocuparam o segundo lugar no ranking de mortalidade por acidente. A cada 34 atropelamentos, ocorreram 10 mortes. Cerca de 4 mil atropelamentos/ano, um a cada duas horas, aproximadamente.
Disponível em: http://www.ipea.gov.br Acesso em: 6 jan. 2009.
De acordo com os dados, se for escolhido aleatoriamente para investigação mais detalhada um dos atropelamentos ocorridos no biênio 2004/2005, a probabilidade de ter sido um atropelamento sem morte é
Se de cada 34 atropelamentos ocorreram 10 mortes, 24 sobrevivem. A probabilidade de ter sido um atropelamento sem morte é:
[tex] \frac{24}{34} = \frac{12}{17} [tex]
(ENEM 2009 - Edição anulada).
Em um determinado semáforo, as luzes completam um ciclo de verde, amarelo e vermelho em 1 minuto e 40 segundos. Desse tempo, 25 segundos são para a luz verde, 5 segundos para a amarela e 70 segundos para a vermelha. Ao se aproximar do semáforo, um veículo tem uma determinada probabilidade de encontrá-lo na luz verde, amarela ou vermelha. Se essa aproximação for de forma aleatória, pode-se admitir que a probabilidade de encontrá-lo com uma dessas cores é diretamente proporcional ao tempo em que cada uma delas fica acesa.
Suponha que um motorista passa por um semáforo duas vezes ao dia, de maneira aleatória e independente uma da outra. Qual é a probabilidade de o motorista encontrar esse semáforo com a luz verde acesa nas duas vezes em que passar?
Se a cada 1 minuto e 40 segundos (100 segundos) a luz verde fica acesa 25 segundos a probabilidade do motorista encontrar a luz verde, ao passar pelo semáforo, é
[tex] \frac{25}{100} = \frac{1}{4} [tex]
A probabilidade de encontrar a luz verde acesa nas duas vezes em que passar é
[tex] \frac{1}{4} \cdot \frac{1}{4} = \frac{1}{16} [tex]
(ENEM 2009 - Edição anulada).
Um dos diversos instrumentos que o homem concebeu para medir o tempo foi a ampulheta, também conhecida como relógio de areia. Suponha que uma cozinheira tenha de marcar 11 minutos, que é o tempo exato para assar os biscoitos que ela colocou no forno. Dispondo de duas ampulhetas, uma de 8 minutos e outra de 5, ela elaborou 6 etapas, mas fez o esquema, representado a seguir, somente até a 4a etapa, pois é só depois dessa etapa que ela começa a contar os 11 minutos.

A opção que completa o esquema é

Para que nas duas últimas etapas a cozinheira possa contar um tempo de 11 minutos ela deve imediatamente inverter a ampulheta II fazendo com que os “3 minutos de areia” que já haviam escoadas, retornem. Ao final desse tempo ela deve imediatamente inverter a amplitude I deixando os “8 minutos de areia” escoarem.
Logo, opção C.
(ENEM 2009 - Edição anulada).
A importância do desenvolvimento da atividade turística no Brasil relaciona-se especialmente com os possíveis efeitos na redução da pobreza e das desigualdades por meio da geração de novos postos de trabalho e da contribuição para o desenvolvimento sustentável regional.

No gráfico são mostrados três cenários – pessimista, previsível, otimista – a respeito da geração de empregos pelo desenvolvimento de atividades turísticas.
De acordo com o gráfico, em 2009, o número de empregos gerados pelo turismo será superior a

Pela leitura direta do gráfico o número de empregos gerados pelo turismo até 2009 está entre 416 000 e 516 000 no cenário pessimista, em torno de 516 000 no cenário previsível e entre 516 000 e 616 000 no cenário otimista.
(ENEM 2009 - Edição anulada).
Pneus usados geralmente são descartados de forma inadequada, favorecendo a proliferação de insetos e roedores e provocando sérios problemas de saúde pública. Estima-se que, no Brasil, a cada ano, sejam descartados 20 milhões de pneus usados. Como alternativa para dar uma destinação final a esses pneus, a Petrobras, em sua unidade de São Mateus do Sul, no Paraná, desenvolveu um processo de obtenção de combustível a partir da mistura dos pneus com xisto. Esse procedimento permite, a partir de uma tonelada de pneu, um rendimento de cerca de 530 kg de óleo.
Disponível em: http://www.ambientebrasil.com.br. Acesso em: 3 out 2008 (adaptado).
Considerando que uma tonelada corresponde, em média, a cerca de 200 pneus, se todos os pneus descartados anualmente fossem utilizados no processo de obtenção de combustível pela mistura com xisto, seriam então produzidas
20 milhões de pneus correspondem a:
[tex] \frac{20\ 000\ 000}{200} = 100\ 000\ de\ toneladas [tex]
Com esta quantidade é possível obter:
= 530 kg ∙ 100 000
= 53 000 000 kg
= 53 mil toneladas de óleo
(ENEM 2009 - Edição anulada).
Uma empresa produz jogos pedagógicos para computadores, com custos fixos de R$ 1.000,00 e custos variáveis de R$ 100,00 por unidade de jogo produzida. Desse modo, o custo total para x jogos produzidos é dado por C(x) = 1 + 0,1 x (em R$ 1.000,00).
A gerência da empresa determina que o preço de venda do produto seja de R$ 700,00. Com isso a receita bruta para x jogos produzidos é dada por R(x) = 0,7x (em R$ 1.000,00). O lucro líquido, obtido pela venda de x unidades de jogos, é calculado pela diferença entre a receita bruta e os custos totais.
O gráfico que modela corretamente o lucro líquido dessa empresa, quando são produzidos x jogos, é

Em milhares de reais o lucro obtido pela venda dos x jogos é dado por:
L(x) = R(x) – C(x)
L(x) = 0,7x – (1 + 0,1x)
L(x) = 0,6x – 1
Logo, o gráfico é o da alternativa B.
(ENEM 2009 - Edição anulada).
Três empresas de táxi W, K e L estão fazendo promoções: a empresa W cobra R$ 2,40 a cada quilômetro rodado e com um custo inicial de R$ 3,00; a empresa K cobra R$ 2,25 a cada quilômetro rodado e uma taxa inicial de R$ 3,80 e, por fim, a empresa L, que cobra R$ 2,50 a cada quilômetro rodado e com taxa inicial de R$ 2,80. Um executivo está saindo de casa e vai de táxi para uma reunião que é a 5 km do ponto de táxi, e sua esposa sairá do hotel e irá para o aeroporto, que fica a 15 km do ponto de táxi.
Assim, os táxis que o executivo e sua esposa deverão pegar, respectivamente, para terem a maior economia são das empresas
A tabela a seguir mostra o custo da corrida, em reais, para o executivo e para sua esposa, cobrado por cada empresa.
W: 5 × 2,40 + 3,00 = R$ 15,00
K: 5 × 2,25 + 3,80 = R$ 15,05
L: 5 × 2,50 + 2,80 = R$ 15,30
W: 15 × 2,40 + 3,00 = R$ 39,00
K: 15 × 2,25 + 3,80 = R$ 37,55
L: 15 × 2,50 + 2,80 = R$ 40,30
Para terem a maior economia o executivo deve pegar o táxi da empresa W e sua esposa o táxi da empresa K.
(ENEM 2009 - Edição anulada).
Uma pessoa decidiu depositar moedas de 1, 5, 10, 25 e 50 centavos em um cofre durante certo tempo. Todo dia da semana ela depositava uma única moeda, sempre nesta ordem: 1, 5, 10, 25, 50, e, novamente, 1, 5, 10, 25, 50, assim sucessivamente.
Se a primeira moeda foi depositada em uma segunda-feira, então essa pessoa conseguiu a quantia exata de R$ 95,05 após depositar a moeda de
A cada cinco dias a pessoa deposita 1 + 5 + 10 + 25 + 50 = 91 centavos.
Para depositar R$ 95,05 (9505 centavos) serão necessários 104 grupos de cinco dias mais quatro dias para depositar 41 centavos, pois 9505 = 91 ∙ 104 + 41.
No total serão necessários 5 ∙ 104 + 4 = 524 dias, correspondendo a 74 semanas completas mais seis dias. Seis dias contados a partir de segunda-feira inclusive, cai no sábado.
(ENEM 2009 - Edição anulada).
Segundo a Associação Brasileira de Alumínio (ABAL), o Brasil foi o campeão mundial, pelo sétimo ano seguido, na reciclagem de latas de alumínio. Foi reciclado 96,5% do que foi utilizado no mercado interno em 2007, o equivalente a 11,9 bilhões de latinhas. Este número significa, em média, um movimento de 1,8 bilhão de reais anuais em função da reutilização de latas no Brasil, sendo 523 milhões referentes à etapa da coleta, gerando, assim, “emprego” e renda para cerca de 180 mil trabalha dores.
Essa renda, em muitos casos, serve como complementação do orçamento familiar e, em outros casos, como única renda da família.
Revista Conhecimento Prático Geografia, n° 22. (adaptado)
Com base nas informações apresentadas, a renda média mensal dos trabalhadores envolvidos nesse tipo de coleta gira em tomo de
A renda anual de cada trabalhador, em reais, é:
[tex] \frac{523\ 000\ 000}{180\ 000} \cong\ 2\ 905,56 [tex]
A renda mensal, também em reais, é aproximadamente de
[tex] \frac{2\ 905,56}{12} = 242,13 \cong\ 242,00 [tex]
(ENEM 2009 - Edição anulada).
Nos últimos anos, o aumento da população, aliado ao crescente consumo de água, tem gerado inúmeras preocupações, incluindo o uso desta na produção de alimentos.
O gráfico mostra a quantidade de litros de água necessária para a produção de 1 kg de alguns alimentos.

Com base no gráfico, para a produção de 100 kg de milho, 100 kg de trigo, 100 kg de arroz, 100 kg de carne de porco e 600 kg de carne de boi, a quantidade média necessária de água, por quilograma de alimento produzido, é aproximadamente igual a
100 kg de milho, 100 kg de trigo, 100 kg de arroz, 100 kg de carne de porco e 600 kg de carne de boi totalizam 1 000 kg de alimento. Para produzi-los são necessários, segundo o gráfico,
100 ∙ (1 000 + 1 500 + 2 500 + 5 000) + 600 ∙ 17 000 = 11 200 000 litros de água
Em média são gastos
[tex] \frac{11\ 200\ 000 L}{1\ 000\ kg} = 11\ 200 [tex] litros de água por quilograma
(ENEM 2009 - Edição anulada).
Uma empresa precisa comprar uma tampa para o seu reservatório, que tem a forma de um tronco de cone circular reto, conforme mostrado na figura.

Considere que a base do reservatório tenha raio [tex]R = 2\sqrt{3}[tex] m e que sua lateral faça um ângulo de 60° com o solo.
Se a altura do reservatório é 12 m, a tampa a ser comprada deverá cobrir uma área de
A figura seguinte representa a secção meridiana do reservatório, com medidas em metros.

No ∆ABE temos:
[tex] tg60° = \frac{AE}{EB} [tex]
[tex] \sqrt{3} = \frac{12}{EB} [tex]
[tex] EB = 4\sqrt{3} [tex]
O raio [tex] \overline{O'B} [tex] da tampa superior mede [tex] 2\sqrt{3} + 4\sqrt{3} = 6\sqrt{3}[tex] e tem área de:
[tex] Área = π \cdot R^{2} = π \cdot (6\sqrt{3})^{2} [tex]
[tex] Área = 108 π\ m^{2} [tex]
(ENEM 2009 - Edição anulada).
A fotografia mostra uma turista aparentemente beijando a esfinge de Gizé, no Egito. A figura a seguir mostra como, na verdade, foram posicionadas a câmera fotográfica, a turista e a esfinge.

Medindo-se com uma régua diretamente na fotografia, verifica-se que a medida do queixo até o alto da cabeça da turista é igual a 2/3 da medida do queixo da esfinge até o alto da sua cabeça. Considere que essas medidas na realidade são representadas por de d e d’, respectivamente, que a distância da esfinge à lente da câmera fotográfica, localizada no plano horizontal do queixo da turista e da esfinge, é representada por b, e que a distância da turista à mesma lente, por a.
A razão entre b e a será dada por

Da semelhança dos triângulos ACF e DCE temos:
[tex] \frac{b}{a} = \frac{d}{c} = \frac{2}{3}d' \cdot \frac{1}{c} = \frac{2d'}{3c} [tex]
pois, conforme o enunciado,
[tex] d = \frac{2}{3}d' [tex]
(ENEM 2009 - Edição anulada).
Uma fotografia tirada em uma câmera digital é formada por um grande número de pontos, denominados pixels.
Comercialmente, a resolução de uma câmera digital é especificada indicando os milhões de pixels, ou seja, os megapixels de que são constituídas as suas fotos.
Ao se imprimir uma foto digital em papel fotográfico, esses pontos devem ser pequenos para que não sejam distinguíveis a olho nu. A resolução de uma impressora é indicada pelo termo dpi (dot per inch) , que é a quantidade de pontos que serão impressos em uma linha com uma polegada de comprimento. Uma foto impressa com 300 dpi, que corresponde a cerca de 120 pontos por centímetro, terá boa qualidade visual, já que os pontos serão tão pequenos, que o olho não será capaz de vê-los separados e passará a ver um padrão contínuo.
Para se imprimir uma foto retangular de 15 cm por 20 cm, com resolução de pelo menos 300 dpi, qual é o valor aproximado de megapixels que a foto terá?
A impressão de uma foto de 15 cm por 20 cm na resolução de pelo menos 300 dpi terá:
(15 ∙ 120) ∙ (20 ∙ 120) pixels
= 4 320 000 pixels = 4,32 megapixels
(ENEM 2009 - Edição anulada).
A taxa anual de desmatamento na Amazônia é calculada com dados de satélite, pelo Instituto Nacional de Pesquisas Espaciais (INPE), de 10 de agosto de um ano a 31 de julho do ano seguinte. No mês de julho de 2008, foi registrado que o desmatamento acumulado nos últimos 12 meses havia sido 64% maior do que no ano anterior, quando o INPE registrou 4.974 km² de floresta desmatada. Nesses mesmos 12 meses acumulados, somente o estado de Mato Grosso foi responsável por, aproximadamente, 56% da área total desmatada na Amazônia.
Jornal O Estado de São Paulo Disponível em: Acesso em 30 ago. 2008 (adaptado).
De acordo com os dados, a área desmatada sob a responsabilidade do estado do Mato Grosso, em julho de 2008, foi
Se em Julho de 2009 foram registrados 4 974 km² de florestas desmatadas, e em Julho de 2008 esse desmatamento foi 64% maior então, nesse ano o desmatamento foi, em km²,
164% ∙ 4974 = 8 157,36
Mato Grosso contribui com 56% ∙ 8157,36 4568, desse total.
(ENEM 2009 - Edição anulada).
Um fazendeiro doa, como incentivo, uma área retangular de sua fazenda para seu filho, que está indicada na figura como 100% cultivada. De acordo com as leis, deve-se ter uma reserva legal de 20% de sua área total. Assim, o pai resolve doar mais uma parte para compor a reserva para o filho, conforme a figura.

De acordo com a figura acima, o novo terreno do filho cumpre a lei, após acrescentar uma faixa de largura x metros contornando o terreno cultivado, que se destinará à reserva legal (filho). O dobro da largura x da faixa é
O novo terreno do filtro tem dimensões (a + x) e (b + x) e a área cultivada corresponde a 80% do total, e (a ∙ b). Dessa forma,
[tex] 80 \%(a +x)\cdot (b +x) = ab [tex]
[tex] 0,8[x^{2} + (a + b)x +ab] = ab [tex]
[tex] 4 x^{2} + 4(a + b)x - ab = 0 [tex]
[tex] x = \frac{-4(a+b)\ \pm\ 4\sqrt{(a+b)^{2} +ab}}{8} [tex]
[tex] x = \frac{\sqrt{(a+b)^{2}\ +\ ab}\ -\ a + b)}{2} [tex]
pois, x > 0.
Assim, o dobro da largura x é:
[tex] 2x = \sqrt{(a+b)^{2} +ab} - (a + b) [tex]
(ENEM 2009 - Edição anulada).
Diante de um sanduíche e de uma porção de batatas fritas, um garoto, muito interessado na quantidade de calorias que pode ingerir em cada refeição, analisa os dados de que dispõe. Ele sabe que a porção de batatas tem 200 g, o que equivale a 560 calorias, e que o sanduíche tem 250 g e 500 calorias. Como ele deseja comer um pouco do sanduíche e um pouco das batatas, ele se vê diante da questão: "Quantos gramas de sanduíche e quantos gramas de batata eu posso comer para ingerir apenas as 462 calorias permitidas para esta refeição?"
Considerando que x e y representam, respectivamente, em gramas, as quantidades do sanduíche e das batatas que o garoto pode ingerir, assinale a alternativa correspondente à expressão algébrica que relaciona corretamente essas quantidades.
As calorias adquiridas pelo consumo de x gramas de sanduíche e y gramas de batatas e
[tex] \frac{500}{250}x + \frac{560}{200}y = 462 [tex]
[tex] 2x + 2,8y = 462 [tex]
(ENEM 2009 - Edição anulada).
Um chefe de cozinha utiliza um instrumento cilíndrico afiado para retirar parte do miolo de uma laranja. Em seguida, ele fatia toda a laranja em secções perpendiculares ao corte feito pelo cilindro. Considere que o raio do cilindro e da laranja sejam iguais a 1 cm e a 3 cm, respectiva mente.

A área da maior fatia possível é
A maior fatia (adotando-se espessura zero) e a que contém o círculo maior da esfera (laranja).
Descontada a secção transversal do cilindro, cuja área e de (π ∙ 12), esta fatia tem área, em cm², de:
π ∙ 32 – π ∙ 12 = 8π
equivalente a oito vezes a área da secção transversal do cilindro.
(ENEM 2009 - Edição anulada).
Depois de jogar um dado em forma de cubo e de faces numeradas de 1 a 6, por 10 vezes consecutivas, e anotar o número obtido em cada jogada, construiu-se a seguinte tabela de distribuição de frequências.

A média, mediana e moda dessa distribuição de frequências são, respectivamente
Colocados em ordem crescente, os resultados obtidos foram
1, 1, 1, 1, 2, 4, 4, 5, 5 e 6
A media foi
[tex] \frac{4 \cdot 1 + 2 \cdot 1 + 2 \cdot 4 + 5 \cdot 2 + 6 \cdot 1 }{10} = \frac{30}{10} = 3 [tex]
A mediana (media entre os dois elementos centrais do Rol) é
[tex] \frac{2+4}{2} = 3 [tex]
A moda, elementos de maior frequência, e 1.
(ENEM 2009 - Edição anulada).
Um vasilhame na forma de um cilindro circular reto de raio da base de 5 cm e altura de 30 cm está parcialmente ocupado por 625π cm³ de álcool. Suponha que sobre o vasilhame seja fixado um funil na forma de um cone circular reto de raio da base de 5 cm e altura de 6 cm, conforme ilustra a figura 1. O conjunto, como mostra a figura 2, é virado para baixo, sendo H a distância da superfície do álcool até o fundo do vasilhame.

Considerando-se essas informações, qual é o valor da distância H?
Em cm², o volume total do vasilhame, incluindo o funil, e de:
[tex] π \cdot 5^{2} \cdot 30 + \frac{π \cdot 5^{2} \cdot 6}{3} = 800π [tex]
O volume do fundo do vasilhame (parte superior apos ter sido virado) e, em cm², tal que:
[tex] π \cdot 5^{2} \cdot H = 800π - 625π [tex]
[tex] 25H = 175 [tex]
[tex] H = 7 [tex]
(ENEM 2009 - Edição anulada).
Uma das expressões artísticas mais famosas associada aos conceitos de simetria e congruência é, talvez, a obra de Maurits Comelis Escher, artista holandês cujo trabalho é amplamente difundido. A figura apresentada, de sua autoria, mostra a pavimentação do plano com cavalos claros e cavalos escuros, que são congruentes e se encaixam sem deixar espaços vazios.

Realizando procedimentos análogos aos feitos por Escher, entre as figuras abaixo, aquela que poderia pavimentar um plano, utilizando-se peças congruentes de tonalidades claras e escuras é

A figura que permite uma pavimentação devera permitir um encaixe perfeito, sem sobreposição e sem deixar sobras.
Da figura apresentadas, apenas a da alternativa D satisfaz tal condição, como se vê no esquema abaixo.

(ENEM 2009 - Edição anulada).
Em um concurso realizado em uma lanchonete, apresentavam-se ao consumidor quatro cartas voltadas para baixo, em ordem aleatória, diferenciadas pelos algarismos 0, 1, 2 e 5. O consumidor selecionava uma nova ordem ainda com as cartas voltadas para baixo. Ao desvirá-las, verificava-se quais delas continham o algarismo na posição correta dos algarismos do número 12,50 que era o valor, em reais, do trio-promoção. Para cada algarismo na posição acertada, ganhava-se R$ 1,00 de desconto. Por exemplo, se a segunda carta da sequência escolhida pelo consumidor fosse 2 e a terceira fosse 5, ele ganharia R$ 2,00 de desconto.
Qual é a probabilidade de um consumidor não ganhar qualquer desconto?
A tabela apresenta as 24 possibilidades de se colocarem as cartas.

Destas, apenas em 9 casos nenhum dos algarismos encontra-se na mesma posição.
Estes números aparecem em destaque na tabela.
A probabilidade de um consumidor não ganhar qualquer desconto é:
[tex] \frac{9}{24} = \frac{3}{8} [tex]
(ENEM 2009 - Edição anulada).
No mundial de 2007, o americano Bernard Lagat, usando pela primeira vez uma sapatilha 34% mais leve do que a média, conquistou o ouro na corrida de 1.500 metros com um tempo de 3,58 minutos. No ano anterior, em 2006, ele havia ganhado medalha de ouro com um tempo de 3,65 minutos nos mesmos 1.500 metros.
Revista Veja, São Paulo, ago. 2008 (adaptado).
Sendo assim, a velocidade média do atleta aumentou em aproximadamente
Sendo [tex]V_{1}[tex] e [tex]V_{2}[tex] a velocidade do atleta, em metros por minuto, em 2006 e 2007 respectivamente, temos:
[tex] 3,65 \cdot V_{1} = 3,58 \cdot V_{2} = 1500 [tex]
[tex] V_{2} = \frac{3,65}{3,58} \cdot V_{1} [tex]
[tex] V_{2} = 1,02 \cdot V_{1} = (1 + 2 \%)V_{1} [tex]
(ENEM 2009 - Edição anulada).
No depósito de uma biblioteca há caixas contendo folhas de papel de 0,1 mm de espessura, e em cada uma delas estão anotadas 10 títulos de livros diferentes. Essas folhas empilhadas formando uma torre vertical de 1 m de altura.
Qual a representação, em potência de 10, correspondente à quantidade de títulos de livros registrados nesse empilhamento?
O total de títulos de livros registrados no empilhamento é:
[tex] \frac{1\ m}{0,1\ mm} \cdot 10 = \frac{10^{3}\ mm}{10^{-1}\ mm} \cdot 10 = 10^{5} [tex]
(ENEM 2009 - Edição anulada).
No quadro seguinte, são informados os turnos em que foram eleitos os prefeitos das capitais de todos os estados brasileiros em 2004.

Na região Norte, a frequência relativa de eleição dos prefeitos no 2º turno foi, aproximadamente,
São capitais da região Norte do Brasil, Belém (PA), Boa Vista (RR), Macapá (AP), Manaus (AM), Palmas (TO), Porto Velho (RO) e Rio Branco (AC).
Dessas, três delas tiveram segundo turno. A saber Belém, Manaus e Porto Velho, correspondendo a:
[tex] \frac{3}{7} \cong 0,4286 = 42,86 \% [tex]
das capitais da região Norte.
(ENEM 2009 - Edição anulada).
A empresa WOTU Cosmético vende um determinado produto x, cujo custo de fabricação de cada unidade é dado por 3x² + 232, e o seu valor de venda é expresso pela função 180x – 116. A empresa vendeu 10 unidades do produto x, contudo a mesma deseja saber quantas unidades precisa vender para obter um lucro máximo.
A quantidade máxima de unidades a serem vendidas pela empresa WOTU para a obtenção do maior lucro é
Considerando que x seja a quantidade de produtos produzidos (e não o nome), (3x² + 232) e (180x – 116) respectivamente o custo de produção e a receita pela venda de todas, temos o lucro:
L(x) = (180x – 116) – (3x² + 232)
L(x) = – 3x² + 180x – 348
que e máximo quando:
[tex] x_{v} = \frac{-b}{2a} = \frac{-(+180)}{2 \cdot (-3)} = 30 [tex]
com ilustra a figura:

(ENEM 2009 - Edição anulada).
Em uma praça pública, há uma fonte que é formada por dois cilindros, um de raio r e altura h₁, e o outro de raio R e altura h₂. O cilindro do meio enche e, após transbordar, começa a encher o outro.

Se [tex] R = r \sqrt{2} [tex] e [tex] h_{2} = \frac{h_{1}}{3} [tex], para encher o cilindro do meio foram necessários 30 minutos, então, para se conseguir encher essa fonte e o segundo cilindro, de modo que fique completamente cheio, serão necessários:
O volume do cilindro mais alto é:
[tex] V_{a} = π \cdot r^{2} \cdot h_{1} [tex]
O volume do cilindro mais baixo é:
[tex] V_{b} = π \cdot R^{2} \cdot h_{2} = π \cdot (r\sqrt{2})^{2} \cdot \frac{h_{1}}{3} = \frac{2 π r^{2}h_{1}}{3} [tex]
O volume da parte interna ao cilindro mais baixo e externa ao cilindro mais alto é:
[tex] V_{e} = V_{a} - V_{b} = π \cdot r^{2} \cdot h_{1} - \frac{2 π r^{2}h_{1}}{3} [tex]
[tex] = \frac{π r^{2}h_{1}}{3} = \frac{V_{a}}{3} [tex]
Dessa forma, se para completar Va são necessários 30 minutos, para completar [tex] V_{e}[tex] são necessários [tex] \frac{30}{3} = 10 [tex] minutos. Assim, para encher a fonte são necessários (30 + 10) = 40 minutos.
(ENEM 2009 - Edição anulada).
Um comerciante contratou um novo funcionário para cuidar das vendas. Combinou pagar a essa pessoa R$ 120,00 por semana, desde que as vendas se mantivessem em torno dos R$ 600,00 semanais e, como um estímulo, também propôs que na semana na qual ele vendesse R$ 1.200,00, ele receberia R$ 200,00, em vez de R$ 120,00.
Ao término da primeira semana, esse novo funcionário conseguiu aumentar as vendas para R$ 990,00 e foi pedir ao seu patrão um aumento proporcional ao que conseguiu aumentar nas vendas. O patrão concordou e, após fazer algumas contas, pagou ao funcionário a quantia de
Se para cada R$ 600,00 a mais nas vendas o comerciante aumenta em R$ 80,00 o pagamento da pessoa, para um aumento de R$ (990,00 – 600,00) = R$ 390,00 nas vendas devera aumentar, em reais, [tex] \frac{390}{600} - 80,00 = 52,00 [tex] o salário semanal da pessoa.
Assim, por semana, a pessoa recebera 120 + 52 = 172 reais.
(ENEM 2009 - Edição anulada).
Uma pesquisa foi realizada para tentar descobrir, do ponto de vista das mulheres, qual é o perfil da parceira ideal procurada pelo homem do séc. XXI. Alguns resultados estão apresentados no quadro abaixo.

Correio Braziliense, 29 jun. 2008 (adaptado).
Se a pesquisa foi realizada com 300 mulheres, então a quantidade delas que acredita que os homens odeiam ir ao shopping e pensa que eles preferem que elas façam todas as tarefas da casa é
Admitindo-se que todas tenham opinado e que o que se pede e “a quantidade delas que acreditam que os homens odeiam ir ao shopping e pensa que eles preferem que elas façam todas as tarefas da casa”, temos:
65% ∙ 300 = 195
e
72% ∙ 300 = 216

Assim,
(195 – x) + x + (216 – x) = 300
x = 111
que estão entre 100 e 120.
(ENEM 2009 - Edição anulada).
Um artista plástico construiu, com certa quantidade de massa modeladora, um cilindro circular reto cujo diâmetro da base mede 24 cm e cuja altura mede 15 cm. Antes que a massa secasse, ele resolveu transformar aquele cilindro em uma esfera.

Analisando as características das figuras geométricas envolvidas, conclui-se que o raio R da esfera assim construída é igual a
Para que o volume do cilindro seja igual ao da esfera, devemos ter:
[tex] V_{E} = V_{C} [tex]
[tex] \frac{4πR^{3}}{3} = π(\frac{24}{2})^{2} \cdot 15 [tex]
[tex] R^{3} = 1620 [tex]
[tex] R = \sqrt[3]{1620} = 3\sqrt[3]{60} [tex]
(ENEM 2009 - Edição anulada).
A empresa SWK produz um determinado produto x, cujo custo de fabricação é dado pela equação de uma reta crescente, com inclinação dois e de variável x. Se não tivermos nenhum produto produzido, a despesa fixa é de R$ 7,00 e a função venda de cada unidade x é dada por – 2x² + 229,76x – 441,84.
Tendo em vista uma crise financeira, a empresa fez algumas demissões. Com isso, caiu em 12% o custo da produção de cada unidade produzida. Nessas condições, a função lucro da empresa pode ser expressa como
O custo pela produção de x pecas é dado por C(x) = 2x + 7,00, pois a equação do custo é “uma reta crescente, com inclinação 2”.
A função venda é – 2x² + 229,76x – 441,84.
A função lucro, após a redução de 12% do custo é:
L(x) = (– 2x² + 229,76x – 441,84) – 88% ∙ (2x + 7,00)
L(x) = (– 2x² + 229,76x – 441,84) – 0,88 ∙ (2x + 7,00)
L(x) = – 2x² + 229,76x – 441,84 – 1,76x – 6,16
L(x) = – 2x² + 228x – 448,00
(ENEM 2009 - Edição anulada).
Dois holofotes iguais, situados em H1 e H2, respectivamente, iluminam regiões H1 H2 circulares, ambas de raio R. Essas regiões se sobrepõem e determinam uma região S de maior intensidade luminosa, conforme figura.

A área da região S, em unidades de área, é igual a

A área da região S e dada por:
[tex] 2 \cdot A_{(setor\ circular\ O_{1}AO_{2}B)} - 2A_{ΔO_{1}AO_{2}} [tex]
Assim,
[tex] A_{S} = [(\frac{\frac{2π}{3} - R^{2}}{2}) - \frac{R^{2}\sqrt{3}}{4}] \cdot 2 = \frac{2πR^{2}}{3} - \frac{\sqrt{3}R^{2}}{2} [tex]
(ENEM 2009 - Edição anulada).
Um casal decidiu que vai ter 3 filhos. Contudo, quer exatamente 2 filhos homens e decide que, se a probabilidade fosse inferior a 50%, iria procurar uma clínica para fazer um tratamento específico para garantir que teria os dois filhos homens.
Após os cálculos, o casal concluiu que a probabilidade de ter exatamente 2 filhos homens é
Admitindo-se que para esse casal a probabilidade do filho ser do sexo masculino (ou feminino) é 50%, a probabilidade deles terem exatamente dois filhos homens e, claro, uma mulher é:
[tex] P = C_{3,2} \cdot 50 \% \cdot 50 \% \cdot 50 \% [tex]
[tex] P = 3 \cdot (0,5)^{3} [tex]
[tex] P = 0,375 = 37,5 \% [tex]
(ENEM 2009 - Edição anulada).
Considere um caminhão que tenha uma carroceria na forma de um paralelepípedo retângulo, cujas dimensões internas são 5,1 m de comprimento, 2,1 m de largura e 2,1 m de altura. Suponha que esse caminhão foi contratado para transportar 240 caixas na forma de cubo com 1 m de aresta cada uma e que essas caixas podem ser empilhadas para o transporte.
Qual é o número mínimo de viagens necessárias para realizar esse transporte?
Admitindo-se que as caixas serão empilhadas de forma organizada e cada pilha não pode ultrapassar a altura da carroceria, no comprimento caberão apenas cinco caixas, na largura duas caixas e na altura duas caixas, como sugere a figura seguinte.

Em cada viagem serão transportadas 5 . 2 . 2 = 20 caixas.
Para transportar as 240 caixas serão necessárias, e suficientes,
[tex] \frac{240}{20} = 12\ viagens [tex]

Nenhum comentário:
Postar um comentário